机器学习：XGBoost 算法

目录

• XGBoost 算法
  • XGBoost 损失函数
  • XGBoost 损失函数的优化求解
  • XGBoost 算法主流程
    • 切分点查找精确贪心算法
    • 切分点查找近似算法
  • XGBoost 算法健壮性优化
    • 稀疏值处理
    • 正则化方法
  • XGBoost 算法运行效率优化
    • 分块并行学习
    • 缓存优化
    • Out-of-core Computation
  • XGBoost 与 GBDT 的区别
  • XGBoost 库安装

XGBoost 算法

XGBoost 损失函数

假设输入训练数据集 \(T = \{ (\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), \cdots, (\mathbf{x}_N, y_N) \}\), \(\mathbf{x}_i \in \mathcal{X} \subset \mathbb{R}^n\), \(\mathcal{X}\) 为输入空间, \(y_i \in \mathcal{Y} \subset \mathbb{R}\), \(\mathcal{Y}\) 为输出空间, 指定损失函数 \(L(y, f(\mathbf{x}))\). 输出强学习器 \(f(\mathbf{x})\). 回顾梯度提升算法框架, 这里以回归问题中的梯度提升树算法 (即MART 模型) 为例. 在每一轮迭代 \(m=1,2,\cdots,M\) 中顺次执行以下操作:

1. 对 \(i=1,2,\cdots,N\), 计算下降方向

\[r_{mi} = - \left[ \frac{\partial L(y_i, f(\mathbf{x}_i))}{\partial f(\mathbf{x}_i)} \right]_{f(\mathbf{x}_i) = f_{m-1}(\mathbf{x}_i)} \]

2. 对 \(\{r_{mi}\}^N_{i=1}\) 拟合一个 CART 回归树, 得到第 \(m\) 个回归树, 确定对应的节点划分区域 \(R_m^j\), \(j=1,2,\cdots,J_m\).
3. 对每个叶节点划分区域 \(j=1,2,\cdots,J_m\) 计算最佳拟合值

\[\gamma^j_m = \arg\min_{c} \sum_{\mathbf{x}_i \in R_m^j}L(y_i, f_{m-1}(\mathbf{x}_i)+\gamma) \]

4. 更新强学习器 (提升树模型)

\[f_{m}(\mathbf{x}) = f_{m-1}(\mathbf{x}) + \sum^{J_m}_{j=1} \gamma_{m}^j I(\mathbf{x} \in R_{m}^j) \]

实际上, 从 GBDT 框架概念上来看, 上述每一轮求解过程分为两步: 即第一步基于残差近似值 \(\{r_{mi}\}^N_{i=1}\) 拟合一颗 CART 回归树得到其对应的叶子节点划分区域 \(R_m^j\), \(j=1,2,\cdots,J_m\), 根据 MSE 最小准则来求解每个区域上的最优输出值, 即在任意区域 \(R^j_m\) 中

\[c^j_m = \arg\min_c \sum_{\mathbf{x} \in R^j_m} (r_{mi} - c)^2 = \text{avg}_{\mathbf{x} \in R^j_m} r_{mi} \]

由此得到区域 \(R^j_m\) 中决策树形式为 \(T(\mathbf{x}; \Theta_m) = \sum^J_{j=1}c^j_m I(\mathbf{x} \in R_m^j)\), 这可看作负梯度方向的近似. 第二步即通过线性搜索确定最速下降法的步长

\[\{\gamma^j_m\}^{J_m}_{j=1} = \arg \min_{\{\gamma^j\}^{J_m}_{j=1}} \sum^N_{i=1} L(y_i, f_{m-1}(\mathbf{x}_i) + \sum^{J_m}_{j=1} \gamma^j I(\mathbf{x} \in R_{m}^j)) \]

其中 \(\gamma^j_m = \beta_m c^j_m\) (具体定义见 GBDT 有关文章). 回归树产生的区域互不相交, 因此可直接简化为上面的步骤 3.

对于 XGBoost 算法, 它期望将上面两步合并在一起, 即一次求解出决策树最优的所有 \(J_m\) 个叶子节点区域和每个叶子节点区域的最优解 \(c_{mj}\). XGBoost 的损失函数是在 GBDT 损失函数 \(L(y, f_{m-1}(\mathbf{x}) + h_m(\mathbf{x}))\) 的基础上加上如下正则项:

\[\Omega(h_m) = \gamma J_m + \frac{\lambda}{2} \sum^{J_m}_{j=1} c_{mj}^2 \]

这里由于前 \(m-1\) 个决策树的正则项是常数, 因此省略. \(J_m\) 是叶子节点的个数, \(c_{mj}\) 是第 \(j\) 个叶子节点的最优值. 最终 XGBoost 的损失函数可以表示为:

\[L_m = \sum^m_{i=1}L(y_i, f_{m-1}(\mathbf{x}_i) + h_m(\mathbf{x}_i)) + \gamma J_m + \frac{\lambda}{2} \sum^{J_m}_{j=1} c_{mj}^2 \]

这里的 \(h_m\) 表示决策树, 即要极小化上面的损失函数, 得到第 \(m\) 个决策树的最优的所有 \(J_m\) 个叶子节点区域和每个叶子节点区域的最优解 \(c_{mj}\), GBDT 是拟合泰勒展开式的一阶导数, 而 XGBoost 是基于损失函数的二阶泰勒展开式来求解,

\[\begin{equation} \begin{aligned} L_m &= \sum^N_{i=1}L(y_i, f_{m-1}(\mathbf{x}_i) + h_m(\mathbf{x}_i)) + \gamma J_m + \frac{\lambda}{2} \sum^{J_m}_{j=1} c_{mj}^2\\ &\approx \sum^N_{i=1} \left[ L(y_i, f_{m-1}(\mathbf{x}_i)) + \frac{\partial L(y_i, f_{m-1}(\mathbf{x}_i))}{\partial f_{m-1}(\mathbf{x}_i)}h_m(\mathbf{x}_i) + \frac{1}{2} \frac{\partial^2 L(y_i, f_{m-1}^2(\mathbf{x}_i))}{\partial f_{m-1}(\mathbf{x}_i)}h_m^2(\mathbf{x}_i) \right] + \Omega(h_m) \end{aligned} \end{equation} \]

把一阶导数和二阶导数分别记作

\[g_{mi} = \frac{\partial L(y_i, f_{m-1}(\mathbf{x}_i))}{\partial f_{m-1}(\mathbf{x}_i)} \]

\[h_{mi} = \frac{\partial^2 L(y_i, f_{m-1}^2(\mathbf{x}_i))}{\partial f_{m-1}(\mathbf{x}_i)} \]

则损失函数可以表示为

\[L_m \approx \sum^N_{i=1} \left[ L(y_i, f_{m-1}(\mathbf{x}_i)) + g_{mi} h_t(\mathbf{x}_i) + \frac{1}{2} h_{mi} h_t^2(\mathbf{x}_i) \right] + + \gamma J_m + \frac{\lambda}{2} \sum^{J_m}_{j=1} c_{mj}^2 \]

损失函数里 \(L(y_i, f_{m-1}(\mathbf{x}_i))\) 是常数, 对最小化无影响, 可以去掉, 同时由于每个决策树的第 \(j\) 个叶子节点的取值最终会是同一个值 \(c_{mj}\), 因此损失函数可以继续化简

\[\begin{equation} \begin{aligned} L_m &\approx \sum^N_{i=1} \left[ g_{mi} h_t(\mathbf{x}_i) + \frac{1}{2} h_{mi} h_t^2(\mathbf{x}_i) \right] + \gamma J_m + \frac{\lambda}{2} \sum^{J_m}_{j=1} c_{mj}^2\\ &= \sum^{J_m}_{j=1} \left[ \sum_{\mathbf{x}_i \in R_{mj}}g_{mi} c_{mj} + \frac{1}{2} \sum_{\mathbf{x}_i \in R_{mj}}h_{mi} c_{mj}^2 \right] + \gamma J_m + \frac{\lambda}{2} \sum^{J_m}_{j=1} c_{mj}^2\\ &= \sum^{J_m}_{j=1} \left[ \sum_{\mathbf{x}_i \in R_{mj}}g_{mi} c_{mj} + \frac{1}{2} \left( \sum_{\mathbf{x}_i \in R_{mj}}h_{mi} + \lambda \right) c_{mj}^2 \right] + \gamma J_m \end{aligned} \end{equation} \]

把每个叶子节点区间样本的一阶导数之和与二阶导数之和单独表示为

\[G_{mj} = \sum_{\mathbf{x}_i \in R_{mj}}g_{mi} \]

\[H_{mj} = \sum_{\mathbf{x}_i \in R_{mj}}h_{mi} \]

最终损失函数可表示为

\[L_m = \sum^{J_m}_{j=1} \left[ G_{mj} c_{mj} + \frac{1}{2} \left( H_{mj} + \lambda \right) c_{mj}^2 \right] + \gamma J_m \]

XGBoost 损失函数的优化求解

关于如何一次求解出决策树最优的所有 \(J_m\) 个叶子节点区域和每个叶子节点区域的最优解 \(c_{mj}\), 可以把它拆分成两个问题:

1. 如果已经求出了第 \(m\) 个决策树的 \(J_m\) 个最优的叶子节点区域, 如何求出每个叶子节点区域的最优解 \(c_{mj}\)?

2. 对当前决策树做子树分裂决策时, 应该如何选择特征和特征值进行分裂, 使得损失函数 \(L_m\) 最小?

对于第 1 个问题, 可以直接基于损失函数对 \(c_{mj}\) 求导并置 \(0\), 即可得到叶子节点区域的最优解:

\[c_{mj} = - \frac{G_{mj}}{H_{mj} + \lambda} \]

对于第 2 个问题, 在 GBDT 中是直接拟合 CART 回归树, 节点分裂使用的是均方误差 (mse, Friedman 对其进行改进给出了新的划分准则 friedman_mse), 而 XGBoost 在这里不使用均方误差, 而是使用贪心法, 在每次分裂时都期望最小化损失函数的误差. 当 \(c_{mj}\) 取最优解时, 原损失函数对应的表达式变形为:

\[L_m = -\frac{1}{2}\sum^{J_m}_{j=1} \frac{G_{mj}^2}{H_{mj} + \lambda} + \gamma J_m \]

假设当前节点左右子树的一阶二阶导数和为 \(G_L\), \(H_L\), \(G_R\), \(H_R\), 则每次进行左右子树分裂时要最大程度地降低损失函数的值, 即最大化下式:

\[\left(-\frac{1}{2}\frac{(G_{L}+G_R)^2}{H_L+H_R + \lambda} + \gamma J_m \right) - \left(-\frac{1}{2}\frac{G_L^2}{H_L + \lambda} -\frac{1}{2}\frac{G_R^2}{H_R + \lambda} + \gamma (J_m+1)\right) \]

即决策树分裂标准不再使用 CART 回归树的均方误差, 而是最大化下式:

\[\max \left[\frac{1}{2}\frac{G_L^2}{H_L + \lambda} + \frac{1}{2}\frac{G_R^2}{H_R + \lambda} - \frac{1}{2}\frac{(G_{L}+G_R)^2}{H_L+H_R + \lambda} - \gamma \right] \]

这里也就是说, 根据上面的损失函数, 每次尝试分裂一个叶节点, 计算分裂后的增益, 选择增益最大的作为左右子树分裂标准. 类似于 ID3 中的信息增益和 CART 树中的基尼指数, 这里的增益计算方式为

\[\text{Gain} = \frac{1}{2}\frac{G_L^2}{H_L + \lambda} + \frac{1}{2}\frac{G_R^2}{H_R + \lambda} - \frac{1}{2}\frac{(G_{L}+G_R)^2}{H_L+H_R + \lambda} - \gamma \]

增益越大, 分裂后目标函数减小的越多.

XGBoost 算法主流程

切分点查找精确贪心算法

输入训练数据集 \(T = \{ (\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), \cdots, (\mathbf{x}_N, y_N) \}\), \(\mathbf{x}_i \in \mathcal{X} \subset \mathbb{R}^n\), \(\mathcal{X}\) 为输入空间, \(y_i \in \mathcal{Y} \subset \mathbb{R}\), \(\mathcal{Y}\) 为输出空间, 最大迭代次数 \(M\), 指定损失函数 \(L(y, f(\mathbf{x}))\), 正则化系数 \(\lambda\), \(\gamma\). 输出强学习器 \(f(\mathbf{x})\). 在每一轮 \(m=1,2,\cdots,M\) 顺次执行以下操作:

• 对 \(i=1,2,\cdots,N\), 计算样本在当前轮损失函数 \(L\) 基于 \(f_{m-1}(\mathbf{x}_i)\) 的一阶导数 \(g_{mi}\), 二阶导数 \(h_{mi}\), 计算所有样本的一阶导数和 \(G_{m} = \sum_{i=1}^{N}g_{mi}\) 和二阶导数和 \(H_{m} = \sum_{i=1}^{N}h_{mi}\).

• 基于当前节点尝试分裂决策树, 默认分数 \(\text{score}=0\), \(G\) 和 \(H\) 为当前需要分裂节点的一阶二阶导数之和. 对特征序号 \(k=1,2,\cdots,K\) 依次执行以下操作:

  1. \(G_L=0\), \(H_L=0\).
  2. 将样本按第 \(k\) 个特征值排序, 依次取出第 \(i\) 个样本并计算当前样本放入左子树后左右子树一阶导数和二阶导数的和:
  \[G_L = G_L + g_{mi}, \ G_R = G - G_L \]
  \[H_L = H_L + h_{mi}, \ H_R = H - H_L \]
  3. 尝试更新最大的分数:
  \[\text{score} = \max (\text{score}, -\frac{1}{2}\frac{G_L^2}{H_L + \lambda} -\frac{1}{2}\frac{G_R^2}{H_R + \lambda} - -\frac{1}{2}\frac{(G_{L}+G_R)^2}{H_L+H_R + \lambda} - \gamma) \]

• 基于最大的 \(\text{score}\) 对应的划分特征和特征值分裂子树.

• 如果最大 \(\text{score}=0\), 则当前决策树建立完毕, 计算所有叶子区域的 \(c_{mj}\) , 得到弱学习器 \(h_m(\mathbf{x}_i)\), 更新强学习器\(f_m(\mathbf{x}_i)\), 进入下一轮弱学习器迭代. 如果最大 \(\text{score} \neq 0\), 则转到第 2 步继续尝试分裂决策树.

上面第 2 步可以看作, 对于每个特征将样本按该特征排序, 先将左子节点置空, 依次从右子节点将样本放入左子节点, 计算相关分数, 最后找到最大的分数得到对应的划分特征和特征值分裂子树.

称这样的方法为切分点查找精确贪心算法 (Exact Greedy Algorithm for Split Finding), 假设树的高度为 \(H\), 特征数为 \(K\), 那么该算法的复杂度为 \(O(HKN\log N)\). 其中, 每次排序为 \(O(N\log N)\), 每个特征都需要排序乘以 \(K\), 树的每一层都需要重新计算乘以 \(H\).

切分点查找近似算法

精确贪心算法采用了枚举的方式便利所有可能的分裂点, 但当数据量庞大, 无法全部存入内存中时, 则不能有效地运行, 据此引入近似算法. 它根据特征分布的分位数 (percentiles of feature distribution) 确定候选切分点, 例如第 \(k\) 个特征确定了 \(l\) 个候选切分点 \(S_k = \{s_{k1},s_{k2},\cdots,s_{kl}\}\), 然后根据候选切分点把相应的样本放入对应的桶 (bucket) 中, 对每个桶中的 \(G\) 和 \(H\) 分别进行累加, 在候选切分点集合上进行精确贪心查找, 从而减少了计算量. 切分点查找近似算法 (Approximate Algorithm for Split Finding) 大致框架如下:

1. 对每一个特征 \(k=1,2,\cdots,K\) 依次确定候选切分点:

   根据特征分布的分位数确定 \(l\) 个候选切分点 \(S_k = \{s_{k1},s_{k2},\cdots,s_{kl}\}\), 确定策略可以选择为全局策略和局部策略, 两种不同的策略产生了两种不同的近似算法变体. 全局策略为在学习每个决策树之前确定候选切分点, 当切分点数足够多时, 和精确的贪心算法性能相当. 局部策略为在决策树每次节点分裂时重新确定候选切分点, 而当切分点数不太多时, 性能就能与精确贪心算法相当. 如下图所示.

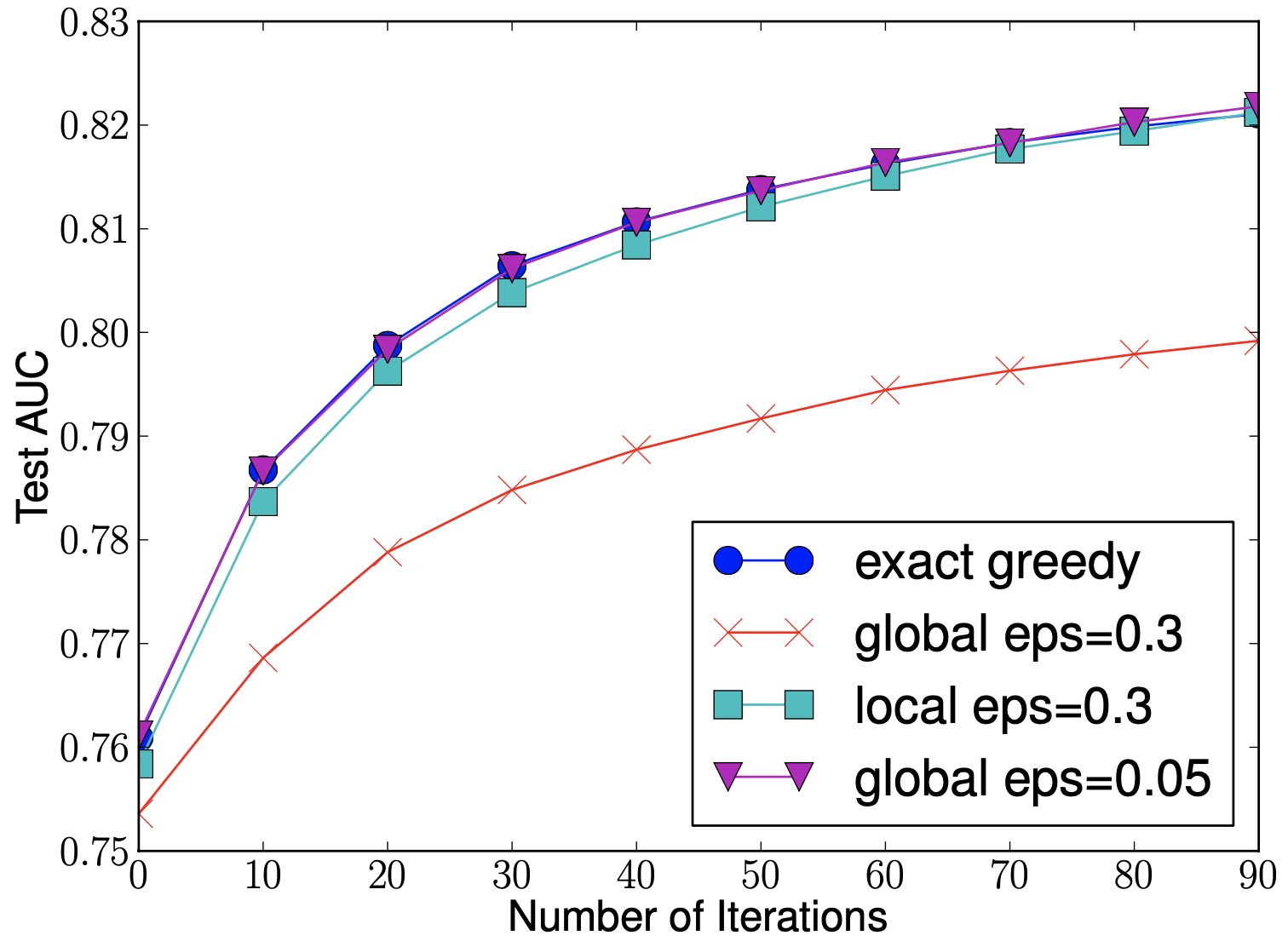
2. 对每一个特征 \(k=1,2,\cdots,K\), 仅基于上一步的候选切分点 \(S_k\) 集合进行精确贪心查找算法, 即计算

   \[G_{kv} = \sum_{j \in \{j|s_{k,v} \geq \mathbf{x}_{jk} \geq s_{k,v-1}\}}g_j \]
   \[H_{kv} = \sum_{j \in \{j|s_{k,v} \geq \mathbf{x}_{jk} \geq s_{k,v-1}\}}h_j \]

   用来代替 \(g_j\) 和 \(h_j\), 与上一节精确贪心查找算法相似, 基于最大的 \(\text{score}\) 对应的划分特征和特征值分裂子树. 近似算法结果与精确贪心算法结果产生误差的原因是, 根据候选切分点装桶后新的聚合统计集合进行精确贪心查找算法得到的切分点与遍历每个原始数据点的切分点不同.

在近似算法中一个重要的步骤是候选切分点的确定, 一般情况下会采用分位数方法使候选切分点均匀分布在数据集上, 但 XGBoost 提出了以二阶梯度 \(h\) 为权重的分位数算法 (Weighted Quantile Sketch).

定义集合 \(\mathcal{D}_k = \{ (\mathbf{x}_{1k},h_1), (\mathbf{x}_{2k},h_2), \cdots, (\mathbf{x}_{nk},h_n)\}\) , 表示每个样本的第 \(k\) 个特征值以及二阶梯度值, 由此定义一个秩函数 (rank function) \(r_k : \mathbb{R} \rightarrow [0,+\infty)\), 表示第 \(k\) 个特征值小于 \(z\) 的样本比例:

\[r_k(z) = \frac{1}{\sum_{(x,h)\in \mathcal{D}_k}h} \sum_{(x,h)\in \mathcal{D}_k, x<z}h \]

切分点 \(S_k = \{s_{k1},s_{k2},\cdots,s_{kl}\}\) 应满足

\[|r_k(s_{k,j})-r_k(s_{k,j+1})|<\varepsilon, \ s_{k1} = \min_{i}x_{ik}, s_{kl} = \max_{i}x_{ik} \]

这里的 \(\varepsilon\) 是近似因子, 即相邻两个候选切分点相差不超过值 \(\varepsilon\), 从此可以判断总共约有 \(1/\varepsilon\) 个候选切分点.

考虑目标函数的泰勒展开

\[\begin{equation} \begin{aligned} L_m &\approx \sum^N_{i=1} \left( g_{i} h_m(\mathbf{x}_i) + \frac{1}{2} h_{i} h_m^2(\mathbf{x}_i) \right) + \Omega(h_m)\\ &= \sum^N_{i=1} \frac{1}{2}h_i\left( 2\frac{g_{i}}{h_{i}} h_m(\mathbf{x}_i) + \frac{1}{2} h_m^2(\mathbf{x}_i) \right) + \Omega(h_m)\\ &= \sum^N_{i=1} \frac{1}{2}h_i\left( \frac{g_i^2}{h_i^2} + 2\frac{g_{i}}{h_{i}} h_m(\mathbf{x}_i) + \frac{1}{2} h_m^2(\mathbf{x}_i) \right) + \Omega(h_m) + \text{constant}\\ &= \sum^N_{i=1} \frac{1}{2}h_i \left( h_m(\mathbf{x}_i) + \frac{g_{i}}{h_{i}} \right)^2 + \Omega(h_m) + \text{constant}\\ \end{aligned} \end{equation} \]

从上式可以看出, 目标函数是真实值为 \(-g_i/h_i\), 权重为 \(h_i\) 的平方损失, 因此使用二阶梯度加权.

XGBoost 算法健壮性优化

稀疏值处理

除了上面讲到的正则化项提高算法的泛化能力外, XGBoost 还对特征的缺失值做了处理. XGBoost 没有假设缺失值一定进入左子树还是右子树, 而是尝试通过枚举所有缺失值在当前节点是进入左子树, 还是进入右子树更优来决定一个处理缺失值默认的方向, 这样处理起来更加的灵活和合理.

也就是说, 上面算法主流程的第 2 步会执行 2 次, 第一次假设特征 \(k\) 所有有缺失值的样本都走左子树, 第二次假设特征 \(k\) 所有缺失值的样本都走右子树, 选择 \(\text{score}\) 最大的情况. 然后针对没有缺失值的特征 \(k\) 的样本走上述流程. 在上面算法主流程中为假设特征 \(k\) 所有有缺失值的样本都走右子树, 而如果是所有的样本走左子树, 则上面计算步骤改为:

\[G_R=0,\ H_R=0 \]

以及

\[G_R = G_R + g_{mi}, \ G_L = G - G_R \]

\[H_R = H_R + h_{mi}, \ H_L = H - H_R \]

正则化方法

与 GBDT 等相同, 在 XGBoost 中也引入了正则化项收缩率 \(\eta\) (shrinkage scale), 也称步长, 有助于防止过拟合

\[f_{m}(\mathbf{x}) = f_{m-1}(\mathbf{x}) + \eta h_m(\mathbf{x}) \]

同时, 列采样技术也有助于防止过拟合, 一种是按层随机方式, 另一种是按树随机方式.

• 按层随机方式: 对于每个决策树同一层内的每个节点, 在分裂之前, 先随机选择一部分特征, 利用这些特征确定最后分割点.
• 按树随机方式: 在构建每个决策树之前, 随机选择一部分特征, 之后所有叶子节点的分裂都使用这些特征, 这种方式也应用于随机森林算法中.

XGBoost 算法运行效率优化

分块并行学习

决策树学习中最耗时的部分是找最优切分点之前数据按特征值排序的过程, 为了减少排序的时间, XGBoost 算法将数据以块 (block) 的形式存储在内存单元 (in-memory units) 中. 每个块中的数据以 CSC (compressed column) 稀疏格式存储, 每个列按相应的特征值排序 (不对缺失值排序), 该排序过程仅在训练之前进行一次, 可以在之后的迭代中重用. 每个块中存储一个或多个特征的值, 并且块中的数据还需储存指向样本的索引.

在精确贪婪算法中, 将整个数据集存储在单个块中, 只需在构造决策树前排序并扫描一次, 就可以收集到所有叶子节点的候选切分点所需的统计信息, 下图说明了上述过程. 精确贪心算法的复杂度为 \(O(HK ||\mathbf{x}||_0 \log N)\), 而使用块结构的精确贪心算法的复杂度为 \(O(HK ||\mathbf{x}||_0 + ||\mathbf{x}||_0 \log N)\), 其中 \(||\mathbf{x}||_0\) 表示训练集中非缺失值的个数. 由此省去每一步中的排序开销.

并行学习的块结构, 块中的每一列按相应的特征值排序, 在块中一列的扫描足以枚举所有分割点

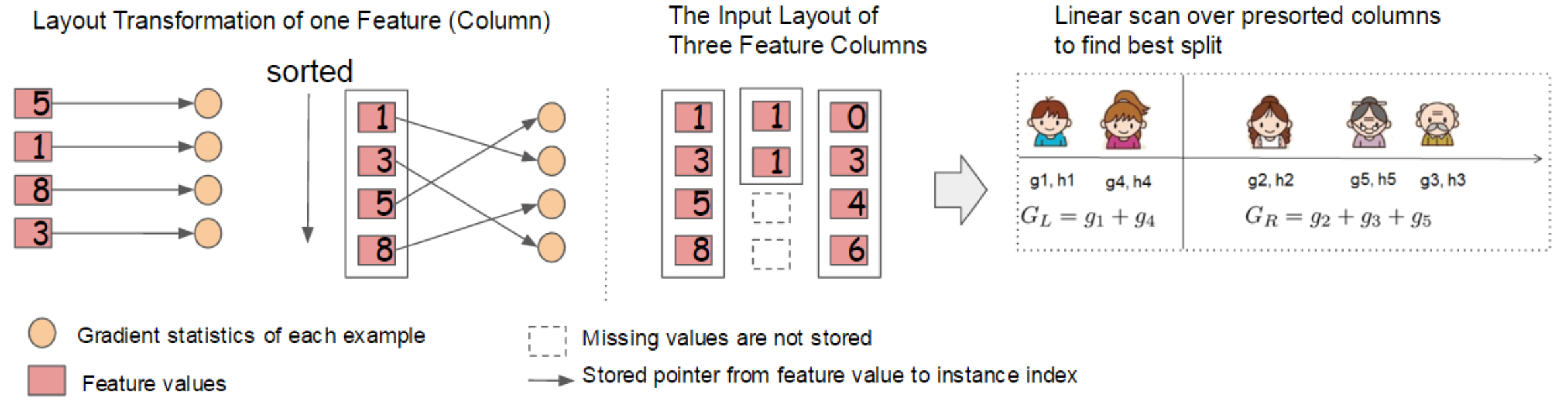
在近似算法中, 可以使用多个块结构, 每个块对应于数据集中的子集, 不同的块可以分布在不同的机器上. 使用这种排序结构, 分位数查找过程转化为对列的线性扫描, 该方法对局部策略尤其有效, 因为它在每次节点分裂时重新确定候选切分点.

缓存优化

在分块并行中, 块储存了排序的列数据, 通过索引建立与原样本数据的一一映射, 由此可以通过索引间接获取梯度统计量, 原始样本数据存放顺序与块中排序后顺序不同, 因此会导致非连续的的内存访问, 即出现内存上的跳跃式查找, 使得 CPU cache 命中率降低.

对于精确贪心算法 (数据集存储在单个块中), 使用缓存预读, 即为每个线程分配一个连续的内存缓冲区 (internal buffer), 读取梯度信息并存入缓冲区中 (由此实现非连续到连续的转化), 该方式有助于减少训练样本数大时的计算开销.

对于近似算法 (数据集存储在多个块中), 通过设置合理的块大小来解决这个问题, 这里定义块的大小为一个块中包含的最多的样本数, 因为它反映了梯度统计量的缓存存储开销. 选择过小的块大小会导致每个线程的工作负载过小, 进而导致低效的并行化, 而过大的块会导致缓存命中率低.

Out-of-core Computation

XGBoost 与 GBDT 的区别

• XGBoost 与 GBDT 同属梯度提升方法 (Gradient Boosting), 相较于 GBDT, XGBoost 是梯度提升方法的一种更为高效的系统性工程实现. 传统的 GBDT 特指梯度提升决策树方法, 仅以 CART 决策树作为基学习器, XGBoost 除了用决策树 (gbtree) 外, 也可以用线性分类器 (gblinear) 作为集学习器.

• GBDT 采用的是数值优化的思想, 即使用最速下降法求解损失函数的最优解, 其中用基学习器拟合下降方向 (损失函数的负梯度), 再通过线性搜索求解步长, 这可以从梯度提升方法的框架看出, 即

  用基学习器拟合下降方向, 得到第 \(m\) 轮基学习器的参数:

  \[\gamma_m = \arg\min_{\beta, \gamma} \sum^N_{i=1} [-\mathbf{g}_m(\mathbf{x}_i)-\beta h(\mathbf{x}_i;\gamma)]^2 \]

  利用线性搜索得到下降步长 (基学习器权重), 使得总体样本损失最小:

  \[\rho_m = \arg\min_{\rho} \sum^N_{i=1} L(y_i, f_{m-1}(\mathbf{x}_i) + \rho b(\mathbf{x}_i,\gamma_m)) \]

  而 XGBoost 采用解析的思维, 直接对损失函数

  \[L_m = \sum^m_{i=1}L(y_i, f_{m-1}(\mathbf{x}_i) + h_m(\mathbf{x}_i)) + \gamma J_m + \frac{\lambda}{2} \sum^{J_m}_{j=1} c_{mj}^2 \]

  展开到二阶近似, 并作为增益建立决策树使得损失函数最小.

• XGBoost 在损失函数中加入了正则项 \(\Omega(h_m) = \gamma J_m + \frac{\lambda}{2} \sum^{J_m}_{j=1} c_{mj}^2\), 包含树的叶子节点个数和叶子节点输出值的平方, 降低模型的方差, 用于控制模型的复杂度. XGBoost 还采用了列采样进一步防止过拟合. 此外, XGBoost 能处理有特征缺失值的数据集, 支持并行运算 (在特征水平上分块并行).

XGBoost 库安装

命令行输入 conda install -c conda-forge xgboost 安装 xgboost 包 (macOS Catalina 10.15.7 with python 3.8).

XGBoost 支持使用 sklearn 风格接口, 方便使用 GridSearchCV 调参.