机器学习:决策树算法(上)
决策树
决策树是一种基本的分类和回归方法. 决策树模型呈树形结构, 在分类问题中, 表示基于特征对实例进行分类的过程, 它可以认为是 if-then 规则的集合, 也可以认为是定义在特征空间与类空间上的条件概率分布. 决策树学习通常包含 3 个步骤: 特征选择, 决策树的生成和决策树的修剪.
模型与学习
分类决策树模型是一种描述对实例进行分类的树形结构. 决策树由节点 (node) 和有向边 (directed edge) 组成. 节点有两种类型: 内部节点 (internal node) 和叶节点 (leaf node), 内部节点表示一个特征或属性, 叶节点表示一个类.
假设给定数据集 \(D = \{ (\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), \cdots, (\mathbf{x}_N, y_N) \}\), 其中 \(\mathbf{x}_i = (x_i^{(1)}, x_i^{(2)}, \cdots, x_i^{(n)})^T\) 为输入实例 (特征向量), \(y_i \in \{ 1,2,\cdots, K \}\) 为类标记, \(N\) 为样本容量. 决策树学习的目标是根据给定的训练数据集构建一个决策树模型, 使它能够对实例进行正确的分类. 当用决策树进行分类时, 从根节点开始, 对实例的某个特征进行测试, 根据测试结果, 将实例分别到其子节点; 这时每个子节点对于着该特征的一个取值, 如此递归直到叶节点, 最后将实例分到叶节点的类中去.
决策树学习本质上是从训练数据集中归纳出一组分类规则, 也可以理解为由训练数据集估计给定特征条件下的条件概率模型. 决策树学习的策略是以损失函数为目标函数的最小化, 其损失函数通常是正则化的极大似然函数. 当损失函数确定后, 学习问题就变为在损失函数意义下选择最优决策树的问题. 但是从所有的决策时中选取最优决策树是 NP 完全问题, 所以现实中通常采用启发式方法, 近似求解这一最优化问题, 得到次最优 (sub-optimal) 的解. 决策树学习算法包含特征选择, 决策树的生成和决策树的修剪三个步骤:
-
特征选择
如果特征数量很多, 可以在决策树学习的开始, 对特征进行选择, 只留下对训练数据有足够分类能力的特征.
-
决策树的生成
决策树学习的算法通常是一个递归地选择最优特征, 并根据该特征对训练数据进行分割, 使得各个子数据集有一个最好的分类, 这个过程对应着特征空间划分, 也对应着决策树的构建. 开始时, 将所有训练数据都放在根节点, 然后选择一个最优特征, 按照这一特征将训练数据集分割成子集, 使得各个子集在当前条件下有一个最好的分类. 如果某个子集里面的数据能够被基本正确分类, 则构建叶节点, 并将这些子集分到所对应的叶节点中; 如果某个子集不能被正确分类, 则继续选择一个新的最优特征, 继续分割数据, 一直递归下去, 直到所有的数据集被正确分类, 或没有合适的特征为止.
-
决策树的剪枝
以上方法对未知的数据未必有好的分类能力, 可能发生过拟合现象, 需要对生成的决策树进行剪枝将树变简单, 使得它有更好的泛化能力. 具体的来说即是去掉过于细分的叶节点, 使其退回父节点甚至更高的节点, 然后将父节点或更高的节点改为新的叶节点.
由于决策树表示一个条件概率模型, 所以深浅不同的决策树对应着不同复杂度的概率模型. 决策树的生成对应于模型的局部选择, 只考虑局部最优, 而决策树的剪枝对应于模型的全局选择, 考虑全局最优.
信息论基础
熵
熵 (entropy) 表示随机变量不确定性的度量, 例如若 \(X\) 是一个取有限个值的离散随机变量, 其概率分布为:
则随机变量 \(X\) 的熵定义为:
再设有随机变量 \((X,Y)\), 其联合概率分布为:
条件熵
条件熵 (conditional entropy) 表示在已知随机变量 \(X\) 条件下随机变量 \(Y\) 的不确定性, 定义为:
可以计算得到:
从此也可以看出条件熵是在已知随机变量 \(X\) 条件下随机变量 \(Y\) 的剩余不确定性的大小.
互信息
两个随机变量的互信息 (mutual information) 是两个变量相互依赖性的度量, 也即两个随机变量的相关性, 定义为:
互信息的直观意义为得知一个新的观测量的信息使得另一个观测量的信息的不确定性减少的程度.

ID3 算法
特征选择: 信息增益
特征选择在于选取对训练集有分类能力的特征, 这样可以提高决策树学习的效率. 如果一个利用一个特征进行分类的效果与随机分类的结果没有很大差别, 则称这个特征是没有分类能力的. 特征选择的准则包括信息增益 (ID3), 信息增益比 (C4.5) 和基尼指数 (CART).
当熵和条件熵中的概率由数据估计 (特别是由极大似然估计) 得到时, 所对应的熵与条件熵分别称为经验熵 (empirical entropy) 和 经验条件熵 (empirical conditional entropy). 信息增益 (information gain) 表示得知特征 \(X\) 的信息而使得类 \(Y\) 的信息不确定性减少的程度.
具体地来说, 特征 \(A\) 对训练数据集 \(D\) 的信息增益 \(g(D,A)\) 定义为集合 \(D\) 的经验熵 \(H(D)\) 与特征 \(A\) 给定条件下 \(D\) 的经验条件熵 \(H(D|A)\) 之差:
决策树学习中的信息增益等价于训练数据集中类与特征的互信息. 一般说互信息时, 两个随机变量的地位相同, 而说信息增益时, 是把其中一个变量看作减小另一个变量不确定度的手段, 二者实际等价.
决策树学习应用信息增益准则选择特征. 给定训练数据集 \(D\) 和 特征 \(A\), 经验熵 \(H(D)\) 表示对数据集 \(D\) 进行分类的不确定性, 而经验条件熵 \(H(D|A)\) 表示在特征 \(A\) 给定条件下对数据集 \(D\) 进行分类的不确定性. 它们的差即信息增益, 表示由于特征 \(A\) 而使得对数据集 \(D\) 分类的不确定性减少的程度. 信息增益依赖于特征, 因此信息增益大的特征具有更强的分类能力.
根据信息增益准则的特征选择方法是: 对训练数据集 (或子集) \(D\), 计算每个特征的信息增益, 比较大小并选择信息增益最大的特征.
ID3 决策树学习算法以信息增益为准则来选择划分属性.
决策树的生成
以 ID3 (Iterative Dichotomiser 3) 为例, 输入为训练样本数据集 \(D\), 离散特征集合 \(A\) 和信息增益的阈值 \(\varepsilon\), 输出为决策树 \(T\). 算法过程如下:
- 判断训练集 \(D\) 中所有实例是否属于同一类 \(c_k\), 如果是则返回单节点树 \(T\), 并标记该节点类别为 \(c_k\).
- 判断特征集 \(A\) 是否为空, 如果是则返回单节点树 \(T\), 标记类别为 \(D\) 中实例数最多的类别.
- 计算 \(A\) 中的各个特征对 \(D\) 的信息增益, 选择信息增益最大的特征 \(A_g\).
- 如果 \(A_g\) 的信息增益小于阈值 \(\varepsilon\), 则返回单节点树\(T\), 标记类别为 \(D\) 中实例数最多的类别.
- 否则, 按特征 \(A_g\) 的每一种取值 \(a_i\) 将 \(D\) 分成若干非空子集 \(D_i\), 将 \(D_i\) 中实例数最大的类作为标记, 构建子节点, 由节点及子节点构成树 \(T\), 返回 \(T\).
- 对所有的子节点, 例如第 \(i\) 个子节点, 以 \(D_i\) 为训练集, \(A-{A_g}\) 为特征集, 递归地调用步骤 1-5, 得到子树 \(T_i\) 并返回.
C4.5 算法
C4.5 算法与 ID3 算法相似, C4.5 算法对 ID3 算法进行了改进, 具体地来说有如下改进:
- ID3 没有考虑连续特征, 只能处理特征具有有限离散值的情况, C4.5 可以处理连续值.
- ID3 以信息增益作为划分训练数据集的特征, 存在偏向于选择取值较多的特征的问题, C4.5 决策树学习算法以信息增益比为准则来选择划分属性.
- ID3 算法没有考虑缺失值的情况, C4.5 可以处理缺失值.
- ID3 没有考虑过拟合的问题, C4.5 引入了正则化系数进行初步的剪枝.
特征选择: 信息增益比
以信息增益作为划分训练数据集的特征, 存在偏向于选择取值较多的特征的问题. 这是因为由于数据集的不充足以及客观存在的大数定律导致取值多的特征在计算条件熵时容易估计出偏小的条件熵. 例如极端情况下某个特征的取值互不相同, 根据特征对训练集进行划分得到的子集个数都为 \(1\), 此时每个子集必定属于某一类, 其经验条件熵为 \(0\), 导致信息增益最大, 这样会使模型变复杂, 导致过拟合.
使用信息增益比 (information gain ratio) 可以对这个问题进行校正, 这是特征选择的另一个准则. 特征 \(A\) 对训练数据集 \(D\) 的信息增益比 \(g_R(D,A)\) 定义为其信息增益 \(g(D,A)\) 与训练数据集关于特征 \(A\) 的值的熵 \(H_A(D)\) 之比:
其中, \(H_A(D) = - \sum^n_{i=1} \frac{|D_i|}{{D}} \log \frac{|D_i|}{{D}}\), \(n\) 为特征 \(A\) 的取值个数.
信息增益比的本质是在信息增益上乘一个惩罚项, 特征个数较多时, 惩罚项较小, 反之则较大. 但信息增益比的缺点是偏向取值较小的特征, 因为此时 \(H_A(D)\) 较大. 解决方法一般先从候选划分属性中找出信息增益高于平均水平的属性, 然后从中选择信息增益比最高的.
C4.5 决策树学习算法以信息增益比为准则来选择划分属性.
连续值处理
C4.5 采用二分法对连续属性进行处理. 给定样本集 \(D\) 和连续属性 \(a\), 假定 \(a\) 在 \(D\) 上出现了 \(n\) 个不同的取值, 将其递增排序记为 \(\{ a^1,a^2,\cdots, a^n \}\). 基于划分点 \(t\) 可以将 \(D\) 分为子集 \(D_t^-\) 和 \(D_t^+\), 其中 \(D_t^-\) 包含那些在属性 \(a\) 上取值不大于 \(t\) 的样本. 可以把区间 \([a^i,a^{i+1})\) 中位点作为候选划分点 (\(t\) 在其中任意值所产生的划分结果相同):
此时可以直接将信息增益比改为样本集 \(D\) 基于划分点 \(t\) (离散值, 共 \(n-1\) 个划分点) 后的信息增益比. 要注意的是, 与离散属性不同, 如果当前节点为连续属性, 则该属性后面还可以参与子节点的产生选择过程.
缺失值处理
给定训练集 \(D\) 和特征 \(A\), 令 \(\tilde{D}\) 表示 \(D\) 中在特征 \(A\) 中没有缺失值的样本子集. 假定特征 \(A\) 有 \(V\) 个可取值 \(\{a^1,a^2,\cdots,a^V\}\), 令 \(\tilde{D}^v\) 表示 \(\tilde{D}\) 中在特征 \(A\) 上取值为 \(a^v\) 的样本子集, \(\tilde{D}_k\) 表示 \(\tilde{D}\) 中属于第 \(k\) 类 (\(k=1,2,\cdots,K\)) 的样本子集, 显然有 \(\tilde{D} = \cup ^K_{k=1} \tilde{D}_k\) 和 \(\tilde{D} = \cup ^V_{v=1} \tilde{D}^v\). 假定为每个样本赋予一个权重 \(\omega_\mathbf{x}\), 并定义
直观上看, 对特征 \(A\), \(\rho\) 表示无缺失样本所占比例, \(\tilde{p}_k\) 表示无缺失样本中第 \(k\) 类所占比例, \(\tilde{r}_v\) 表示无缺失样本中在特征 \(A\) 中取值为 \(a^v\) 的样本所占比例, 且有 \(\sum^K_{k=1}\tilde{p}_k = 1\) 和 \(\sum^V_{v=1}\tilde{r}^v = 1\).
可以将信息增益推广为:
- 如何在属性缺失情况下进行特征划分?
在属性缺失情况下, 仅根据 \(D\) 中在特征 \(A\) 中没有缺失值的样本子集 \(\tilde{D}\) 来判断属性的优劣, 即通过 \(\tilde{g}(D,A)\) 计算, 上面的计算式乘号右边可看作为 \(\tilde{D}\) 上的信息增益.
- 给定划分特征, 若样本在该特征上的值缺失, 如何对样本进行划分?
若样本 \(\mathbf{x}\) 在划分特征 \(A\) 上的取值已知, 则将 \(\mathbf{x}\) 划入与其取值对应的子节点, 且样本权值在子节点中保持为 \(\omega_\mathbf{x}\).
若样本 \(\mathbf{x}\) 在划分特征 \(A\) 上的取值未知, 则将 \(\mathbf{x}\) 同时划入所有子节点, 且样本权值在与特征取值为 \(a^v\) 对应的子节点中调整为 \(\tilde{r}_v \cdot \omega_\mathbf{x}\), 直观的来看就是让同一个样本以不同的概率划入到不同的子节点中去. 例如假设缺失特征 \(A\) 的某样本 \(\mathbf{x}\) 之前权重为 \(\omega_\mathbf{x} = 1\), 特征 \(A\) 有 3 个特征值 \(a^1\), \(a^2\), \(a^3\), 这 3 个特征值对应的无缺失 \(A\) 特征的实例个数分别为 2, 3, 4, 则将 \(\mathbf{x}\) 同时划分进 \(a^1\), \(a^2\), \(a^3\), 对应的权重调整为 \(2/9\), \(3/9\), \(4/9\). 通过这种方式可以有效利用缺失部分特征的样本, 在未缺失数据的特征处可以并入 \(\tilde{g}(D,A)\) 的计算.
- 决策树构造完成后, 如果测试样本特征缺失, 如何确定该样本类别?
若测试样本进入某个特征值未知的分支节点, 则探索所有可能的分类路径, 此时分类结果变为类别的分布, 选择概率最高的类别作为预测结果. 以 Quinlan 原著中的数据集举例,
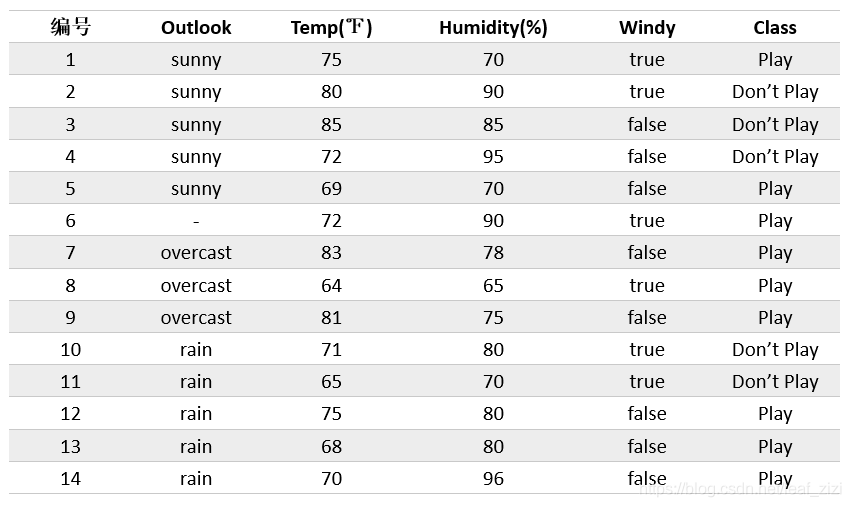
这里的编号 6 样本的 Outlook 特征缺失, 用缺失特征情况下的计算方法可以得到如下决策树, 括号内表示样本的权重等比分配到 Outlook 3 种特征取值节点下, 默认权重为 \(1\):
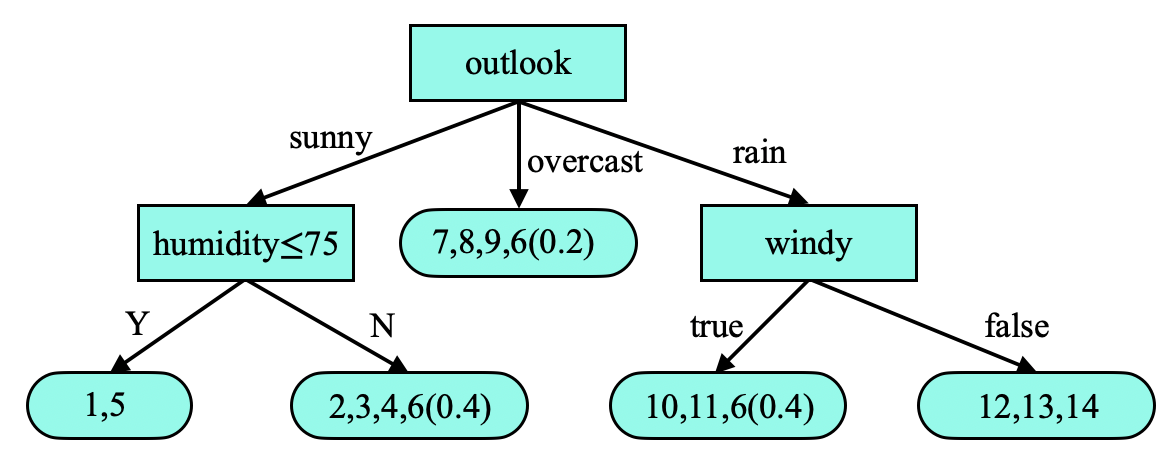
对树的结构进行改进, 每个叶子节点另外储存分类错误率, 下面括号内的数字是权值的累加, 括号中前者表示与该叶节点类别不同的样本数, 后者表示该叶节点包含总样本数, 决策树变为如下:

现在利用这个决策树对测试样本分类, 样本的特征值为: outlook=sunny, temperature=70, humidity=?, windy=false. 样本在 humudity 的两个分支都会考虑: 如果 humudity \(\leq 75\), 类别为 Play; 否则类别为 Don't Play 的概率为 \((3/3.4)=88\%\), 类别为 Play 的概率为 \((0.4/3.4)=12\%\). humidity 中进入 Play 分支的概率为 \(2/5.4\), 那么 Play 的总概率为: \(2/5.4 \times 100 \% + 3.4/5.4 \times 12\% = 44 \%\).
决策树的剪枝
决策树生成算法递归地产生决策树, 直到无法继续进行, 这样会产生过拟合现象. 解决该问题的办法是剪枝, 决策树的剪枝往往通过极小化决策树整体的损失函数 (loss function) 或代价函数 (cost function) 来实现.
设树 \(T\) 的叶节点个数为 \(|T|\), \(t\) 是树 \(T\) 的叶节点, 叶节点有 \(N_t\) 个样本点, 其中 \(k\) 类的样本点有 \(N_{tk}\) 个, \(H_t(T)\) 为叶节点 \(t\) 上的经验熵, \(\alpha \geq 0\) 为参数, 则决策树的损失函数可以定义为:
其中经验熵为:
其中, \(C(T)\) 表示模型对训练数据的预测误差 (例如当 \(\frac{N_{ik}}{N_t}=1\) 时该叶节点完全预测正确, \(H_t(T)\) 最小), \(|T|\) 表示模型复杂度.
决策树的剪枝算法过程如下, 输入生成算法产生的整个树 \(T\) 以及参数 \(\alpha\), 输出修剪后的子树 \(T_{\alpha}\):
- 计算每个叶节点的经验熵.
- 递归地从叶节点向上回缩.
- 设一组叶节点回缩到其父节点之前与之后的整体树分别为 \(T_B\) 和 \(T_A\), 其对应的损失函数分别为 \(C_{\alpha}(T_B)\) 和 \(C_{\alpha}(T_A)\), 若有 \(C_{\alpha}(T_A) \leq C_{\alpha}(T_B)\), 则进行剪枝, 即将父节点变为新的叶节点.
- 返回第 2 步, 直至不能继续为止, 得到损失函数最小的子树 \(T_{\alpha}\).
ID3 算法 python 实现
ID3 决策树算法利用信息增益为准则来选择划分特征, 它只能处理离散特征值, 并且没有剪枝过程. 以贷款申请样本数据为例, 希望学习一个贷款申请的决策树. 先创建一个训练样本集:
# 创建数据集, 最后一列为类别
def create_dataset():
dataset = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
feature_descrip = ['年龄', '有工作', '有自己的房子', '信贷情况']
return dataset, feature_descrip
递归地创建 ID3 决策树, 利用以信息增益为准则来选择划分特征.
# 递归地创建决策树
def creat_tree(dataset, feat_descrip):
# 类别向量
class_list = [data[-1] for data in dataset]
# 当所有实例属于同一类
if class_list.count(class_list[0]) == len(class_list):
return class_list[0]
# 当特征集为空 (因为每轮都会 split dataset, 最后只剩 label)
if len(dataset[0]) == 1:
return majority_cnt(class_list)
# 根据信息增益决定当前最优特征
best_feat_idx = choose_best_feature(dataset)
best_feat_descrip = feat_descrip[best_feat_idx]
# 字典形式保存根节点
decision_tree = {best_feat_descrip: {}}
# 删除已使用的特征
del(feat_descrip[best_feat_idx])
# 得到训练集最优特征的所有取值
feat_values = [data[best_feat_idx] for data in dataset]
unique_values = set(feat_values)
# 遍历所有取值, 递归创建决策树
for value in unique_values:
dataset_split = split_dataset(dataset, best_feat_idx, value)
decision_tree[best_feat_descrip][value] = \
creat_tree(dataset_split, feat_descrip)
return decision_tree
下面是需要用到的子函数:
import math
# 计算给定数据集的经验熵
def calc_entropy(dataset):
num_entries = len(dataset)
label_counts = {}
for data in dataset:
cur_label = data[-1]
label_counts[cur_label] = label_counts.get(cur_label, 0) + 1
entropy = 0.0
for key in label_counts:
prob = float(label_counts[key]) / num_entries
entropy -= prob * math.log(prob, 2)
return entropy
# 按照给定特征划分数据集, 即删除已使用特征列
def split_dataset(dataset, axis, value):
ret_dataset = []
for data in dataset:
if data[axis] == value:
data_reduced = data[:axis]
data_reduced.extend(data[axis+1:])
ret_dataset.append(data_reduced)
return ret_dataset
# 根据信息增益选择最优特征
def choose_best_feature(dataset):
num_feature = len(dataset[0]) - 1
base_entropy = calc_entropy(dataset)
best_info_gain = 0.0
best_feature = -1
for i in range(num_feature):
feature_list = [data[i] for data in dataset]
unique_vals = set(feature_list)
new_entropy = 0.0
for value in unique_vals:
sub_dataset = split_dataset(dataset, i, value)
prob = len(sub_dataset) / float(len(dataset))
new_entropy += prob * calc_entropy(sub_dataset)
info_gain = base_entropy - new_entropy
print("第%d个特征的增益为%.3f" % (i, info_gain))
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = i
return best_feature
# 统计类别向量中出现最多的类别
def majority_cnt(class_list):
# 将每个类别与出现次数保存在 class_count 字典中
class_count = {}
for vote in class_list:
class_count[vote] = class_count.get(vote, 0) + 1
# 根据 value 排序, 返回 (key, value) 对
sorted_class_count = sorted(class_count.items(),
key=lambda x: x[1], reverse=True)
return sorted_class_count[0][0]
可以利用 python 的 pickle 模块储存决策树.
import pickle
# 序列化对象存储决策树
def store_tree(input_tree, filename):
with open(filename, "wb") as fw:
pickle.dump(input_tree, fw)
# 读取决策树
def grab_tree(filename):
fr = open(filename, "rb")
return pickle.load(fr)
if __name__ == "__main__":
dataset, feat_descrip = create_dataset()
decision_tree = creat_tree(dataset, feat_descrip)
store_tree(decision_tree, "classifier_id3.txt")
decision_tree = grab_tree("classifier_id3.txt")
print(decision_tree)
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号