09 决策树-XGBoost算法
1、Xgboost介绍
1.1、Xgboost概述
XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
1.2、青出于蓝
说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。两者都是boosting方法。
2、Xgboost树的定义
2.1、构造决策树
先来举个例子,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
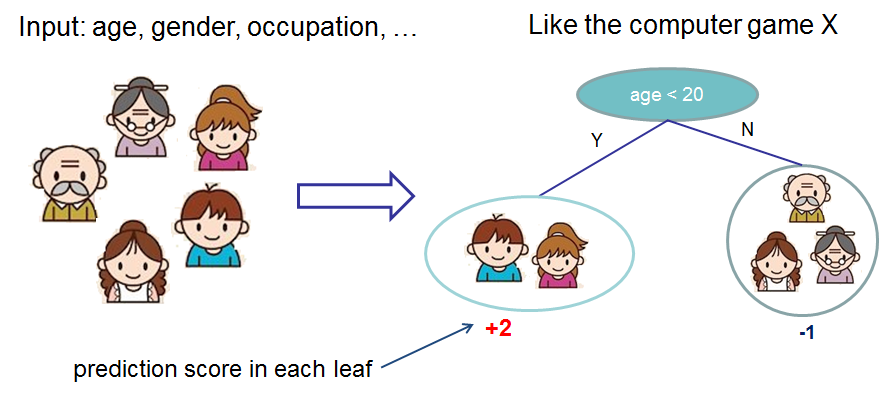
2.2、决策树集成
就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:

恩,你可能要拍案而起了,惊呼,这不是跟之前介绍的GBDT乃异曲同工么?
事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同仅仅在于目标函数的定义。
3、Xgboost目标函数
3.1、目标函数方程
对于Boosting算法我们知道,是将多个弱分类器的结果结合起来作为最终的结果来进行输出。\(f_t(x_i)\)为第 t 棵树的输出结果,\(\hat{y}_i^{(t)}\)是模型当前的输出结果,\(y_i\) 是实际的结果。
那么:
\(\hat{y}_i^{(t)} = \sum\limits_{t=1}^t f_{t}(x_i)\)
\(\hat{y}_i^{(t)} = \hat{y}_i^{(t-1)} + f_t(x_i)\)
XGBoost的目标函数如下图所示:
\(Obj^{(t)} = \sum\limits_{i = 1}^nL(y_i,\hat{y}_i) + \sum\limits_{i =1}^t\Omega(f_t)\)
-
训练损失
\(\sum\limits_{i = 1}^nL(y_i,\hat{y}_i)\)
-
常见损失函数
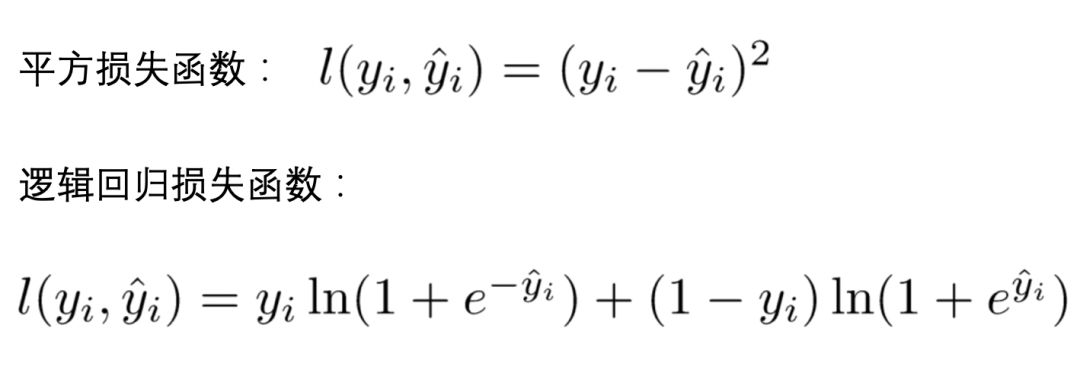
-
树的复杂度
\(\sum\limits_{i =1}^t\Omega(f_i)\)
Xgboost包含多棵树,定义每棵树的复杂度:
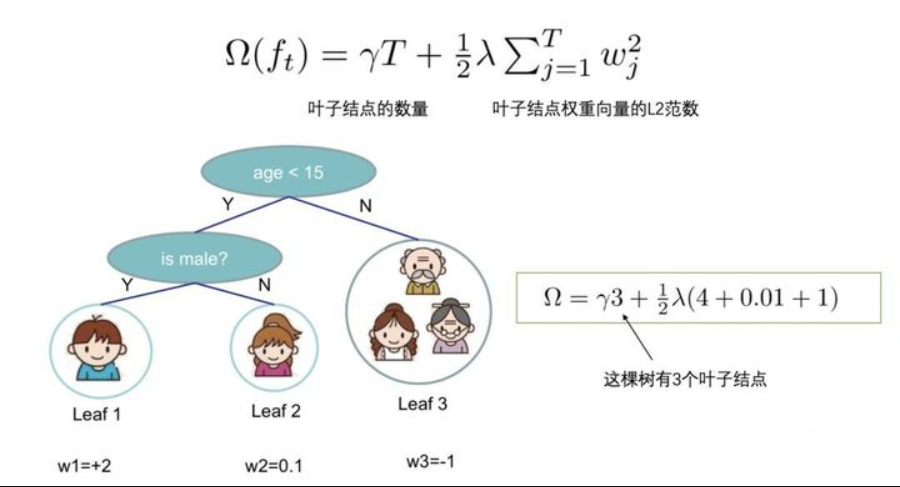
\(\Omega(f) = \gamma T + \frac{1}{2}\lambda \sum\limits_{j=1}^T w_j^2\)
其中 T 为叶子节点的个数,为叶子节点向量的模 。\(\gamma\) 表示节点切分的难度,\(\lambda\) 表示L2正则化系数。
\(Obj^{(t)} = \sum\limits_{i = 1}^nL(y_i,\hat{y}_i^{(t-1)} + f_t(x_i)) + \sum\limits_{i =1}^t\Omega(f_i)\)
\(Obj^{(t)} = \sum\limits_{i=1}^nL(y_i,\hat{y}_i^{(t-1)} + f_t{(x_i})) + \Omega(f_t) + \sum\limits_{i=1}^{t-1}\Omega(f_i)\)
\(Obj^{(t)} = \sum\limits_{i=1}^nL(y_i,\hat{y}_i^{(t-1)} + f_t{(x_i})) + \Omega(f_t) + constant\)
\(\sum\limits_{i=1}^{t-1}\Omega(f_i)\) 为前 t-1 棵树的复杂度,是常数项,求导时可忽略。目标函数简化为:
\(Obj^{(t)} = \sum\limits_{i=1}^nL\left(y_i,\hat{y}_i^{t-1} + f_t{(x_i})\right) + \Omega(f_t)\)
3.2、目标函数泰勒展开
泰勒展开近似目标函数:
\(f(x + \Delta x) \approx f(x) + f'(x)\Delta x + \frac{1}{2}f''(x)\Delta x^2\)
令:
\(g_i = \partial_{\hat{y}^{(t-1)}}l(y,\hat{y}^{(t-1)})\)
\(h_i = \partial^2_{\hat{y}^{(t-1)}}l(y,\hat{y}^{(t-1)})\)
则:
\(Obj^{t} \approx \sum\limits_{i=1}^n\left[ l(y_i,\hat{y}_i^{(t-1)}) + g_if_t(x_i) + \frac{1}{2}h_if^2_t(x_i)\right] + \Omega(f_t)\)
- 方程中的 $$l$$ 即为损失函数(比如平方损失函数:$$l(y_i,\hat{y_i}) = (y_i - \hat{y_i})^2$$,或者交叉熵Log-loss
- \(\Omega(f_t)\) 的是正则项(包括L1正则、L2正则),防止过拟合,鲁棒性加强。
- 对于 f(x),XGBoost利用二阶泰勒展开三项,做一个近似。f(x)表示的是其中一颗回归树。
由于在第 \(t\) 步时 \(\hat{y}_i^{(t-1)}\)其实是一个已知的值,所以 \(l(y_i,\hat{y}_i^{(t-1)})\) 是一个常数,其对函数的优化不会产生影响。因此,去掉全部的常数项,得到目标函数为:
\(Obj^{t} \approx \sum\limits_{i=1}^n\left[g_if_t(x_i) + \frac{1}{2}h_if^2_t(x_i)\right] + \Omega(f_t)\)
\(g_i = \partial_{\hat{y}^{(t-1)}}l(y,\hat{y}^{(t-1)})\)
\(h_i = \partial^2_{\hat{y}^{(t-1)}}l(y,\hat{y}^{(t-1)})\)
所以我们只需要求出每一步损失函数的一阶导和二阶导的值(由于前一步的 \(\hat{y}^{(t-1)}\) 是已知的,所以这两个值就是常数),然后最优化目标函数,就可以得到每一步的 \(f(x)\) ,最后根据加法模型得到一个整体模型。
3.3、定义一棵树
我们重新定义一颗树,包括两个部分:
- 叶子结点的权重向量 \(w\);
- 实例 ---> 叶子结点的映射关系q(本质是树的分支结构);
一棵树的表达形式定义如下:

3.4、定义树的复杂度
我们定义一颗树的复杂度 \(\Omega\),它由两部分组成:
- 叶子结点的数量;
- 叶子结点权重向量的L2范数;
3.5、叶结点归组
我们将属于第 j 个叶子结点的所有样本 xi , 划入到一个叶子结点样本集中,数学表示如下:
\(I_j = {i|q(x_i) == j}\)
然后,将【3】和【4】中一棵树及其复杂度的定义,带入到【2】中泰勒展开后的目标函数 Obj 中,具体推导如下:
\(\begin{aligned}Obj^{(t)} &\approx \sum\limits_{i=1}^n\left[g_if_t(x_i) + \frac{1}{2}h_if^2_t(x_i)\right] + \Omega(f_t)\\\\ &= \sum\limits_{i=1}^n\left[g_iw_{q(x_i) }+\frac{1}{2}h_iw^2_{q(x_i)}\right] + \gamma T +\frac{1}{2}\lambda\sum\limits_{j = 1}^Tw_j^2\\\\ &=\sum\limits_{j=1}^T\left[(\sum\limits_{i \in I_j}g_i)w_j + \frac{1}{2}(\sum\limits_{i \in I_j}h_i + \lambda)w_j^2\right] + \gamma T\end{aligned}\)
所有的训练样本,按叶子结点进行了分组!
为了进一步简化上式,我们定义:
\(G_j = \sum\limits_{i \in I_j}g_i\)
\(H_j = \sum\limits_{i \in I_j}h_i\)
含义如下:
- \(G_j\) :叶子结点 j 所包含样本的一阶偏导数累加和,是一个常量
- \(H_j\) :叶子结点 j 所包含样本的二阶偏导数累加和,是一个常量
将 \(G_j\) 和 \(H_j\) 带入目标式 Obj,得到我们最终的目标函数(注意,此时式中的变量只剩下第 t 棵树的权重向量 w)
\(\begin{aligned}Obj^{(t)} &=\sum\limits_{j=1}^T\left[(\sum\limits_{i \in I_j}g_i)w_j + \frac{1}{2}(\sum\limits_{i \in I_j}h_i + \lambda)w_j^2\right] + \gamma T\\\\&=\sum\limits_{j = 1}^T\left[G_jw_j + \frac{1}{2}(H_j + \lambda)w^2_j\right] + \gamma T\end{aligned}\)
3.6、树结构得分
回忆一下高中数学知识。假设有一个一元二次函数,形式如下:
\(Gx + \frac{1}{2}Hx^2, H > 0\)
我们可以套用一元二次函数的最值公式轻易地求出最值点:
\(x^* = -\frac{b}{2a} = \frac{G}{H}\)
那么回到XGBoost的最终目标函数上 \(Obj^{(t)}\) ,该如何求出它的最值呢?
\(Obj^{(t)} = \sum\limits_{j = 1}^T\left[G_jw_j + \frac{1}{2}(H_j + \lambda)w^2_j\right] + \gamma T\)
我们先简单分析一下上面的式子:
- 对于每个叶子结点 ,可以将其从目标函数中拆解出来:
\(G_jw_j + \frac{1}{2}(H_j + \lambda)w_j^2\)
在【3.5、叶结点归组】中我们提到,\(G_j\) 和 \(H_j\) 相对于第 t 棵树来说是可以计算出来。那么,这个式子就是一个只包含一个变量叶子结点权重 \(w_j\) 的一元二次函数,我们可以通过最值公式求出它的最值点。也可以参考一元二次方程求根公式。

-
两个不同实根:\(x_{1,2} = \frac{-b\ \ \pm\ \ \sqrt{\Delta}}{2a} = \frac{-b \ \ \pm \ \ \sqrt{b^2 - 4ac}}{2a}\)
-
两个相等实根:\(x_{1,2} = -\frac{b}{2a}\)
再次分析一下目标函数 \(Obj^{(t)}\) ,可以发现,各个叶子结点的目标子式是相互独立的,也就是说,当每个叶子结点的子式都达到最值点时,整个目标函数 \(Obj^{(t)}\) 才达到最值点。
那么,假设目前树的结构已经固定,套用一元二次函数的最值公式,将目标函数对 \(w_j\) 求一阶导,并令其等于 0 ,则可以求得叶子结点 \(j\) 对应的权值:
\(w^*_j = -\frac{G_j}{H_j + \lambda}\)
所以目标函数可以化简为:
\(\begin{aligned}Obj^{(t)} &= \sum\limits_{j = 1}^T\left[G_jw_j + \frac{1}{2}(H_j + \lambda)w^2_j\right] + \gamma T\\\\&=\sum\limits_{j = 1}^T\left[-\frac{G_j^2}{H_j + \lambda} +\frac{1}{2}\frac{G_j^2}{H_j + \lambda} \right] + \gamma T\\\\&=-\frac{1}{2}\sum\limits_{j = 1}^T\frac{G_j^2}{H_j + \lambda} + \gamma T\end{aligned}\)

上图给出目标函数计算的例子,求每个节点每个样本的一阶导数 \(g_j\) 和二阶导数 \(h_j\) ,然后针对每个节点对所含样本求和得到 \(G_j\) 和 \(H_j\) ,最后遍历决策树的节点即可得到目标函数。
3.7、XGBoost与GBDT差异
4、Xgboost模型使用
4.1、模型基本使用
4.1.1、使用方式一
import numpy as np
import xgboost as xgb
from xgboost import XGBClassifier
from sklearn import datasets
from sklearn import tree
from sklearn.model_selection import train_test_split
X,y = datasets.load_wine(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
model = XGBClassifier(learning_rate =0.1,# 学习率,控制每次迭代更新权重时的步长,默认0.3。值越小,训练越慢。
n_estimators=10,# 总共迭代的次数,即决策树的个数
max_depth=5, # 深度
min_child_weight= 1,# 默认值为1,。值越大,越容易欠拟合;值越小,越容易过拟合
gamma=0.3,# 惩罚项系数,指定节点分裂所需的最小损失函数下降值。
subsample=0.8,# 训练每棵树时,使用的数据占全部训练集的比例。默认值为1,典型值为0.5-1。防止overfitting。
colsample_bytree=0.8,
objective= 'binary:logistic',# 目标函数
eval_metric = ['merror'],# 验证数据集评判标准
nthread=4,)# 并行线程数
eval_set = [(X_test, y_test),(X_train,y_train)]
model.fit(X_train,y_train,eval_set = eval_set,verbose = True)
model.score(X_test,y_test)
XGBoost可视化
xgb.to_graphviz(model,
condition_node_params={'shape': 'box',
'style': 'filled,rounded',
'fillcolor': '#78bceb'},
leaf_node_params={'shape': 'box',
'style': 'filled,rounded',
'fillcolor': '#e48038'})
4.1.2、使用方式二
X,y = datasets.load_wine(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
param = {'learning_rate':0.1,
'n_estimators':10000,
'max_depth':5,
'min_child_weight':1,
'gamma':0.3,
'subsample':0.8,
'colsample_bytree':0.8,
'verbosity':0,
'objective':'multi:softprob',
'eval_metric':'merror',
'early_stopping_rounds':20}
model = xgb.XGBClassifier(**param)
model.fit(X_train, y_train,eval_set=[(X_test, y_test)])
model.score(X_test,y_test)
4.1.3、使用方式三
DMatrix是XGBoost中使用的数据矩阵。DMatrix是XGBoost使用的内部数据结构,它针对内存效率和训练速度进行了优化
import xgboost as xgb
from sklearn.metrics import accuracy_score
from sklearn import datasets
X,y = datasets.load_wine(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
# 创建数据
dtrain = xgb.DMatrix(data = X_train,label = y_train)
dtest = xgb.DMatrix(data = X_test,label = y_test)
# 指定参数
param = {'learning_rate':0.1,
'max_depth':5,
'min_child_weight':1,
'gamma':0.3,
'subsample':0.8,
'eval_metric':['merror','mlogloss'],
'colsample_bytree':0.1,
'verbosity':0,
'objective':'multi:softmax',
'num_class':3}
num_round = 1000
evals = [(dtrain,'train'),(dtest,'eval')]
bst = xgb.train(param,
dtrain,
num_round,
evals = evals,
early_stopping_rounds=10)
# 进行预测
y_ = bst.predict(dtest)
display(y_,accuracy_score(y_test,y_))
考题
- 请简述Adaboost算法的工作原理,特别是在每次迭代中,如何更新样本的权重?
- Adaboost算法在哪些情况下可能会表现不佳,为什么?
- 请解释XGBoost算法的名称中的“XG”是什么意思?
- XGBoost与传统的GBM(Gradient Boosting Machine)相比,有哪些主要的优势?
- 请解释XGBoost中的正则化项如何帮助防止模型过拟合?
- XGBoost中的
learning_rate参数是什么,它如何影响模型的训练和性能? - 请解释XGBoost中的
subsample和colsample_bytree参数的作用,以及它们如何帮助提升模型的性能? - 在XGBoost中,什么是
DMatrix?为什么需要使用它? - 在使用XGBoost进行分类问题时,你可能会看到一个参数
objective='binary:logistic',请解释这个参数的含义。 - Adaboost和XGBoost算法都是基于Boosting原理的集成方法。请解释Boosting的基本原理,以及它与Bagging(如随机森林)的主要区别是什么?
参考答案
-
Adaboost(Adaptive Boosting)算法是一种集成方法,通过组合多个弱分类器来创建一个强分类器。在每次迭代中,Adaboost会更重视那些被前一个分类器错误分类的样本,通过提高这些样本的权重来实现这一目标。然后,这个新的分类器将在更新后的权重上进行训练。
-
Adaboost可能在以下情况下表现不佳:数据包含较多的噪声和异常值,因为Adaboost会尝试拟合每一个样本;数据中的特征与标签之间的关系非常复杂,超出了基分类器的表示能力。
-
XGBoost中的“XG”表示“Extreme Gradient Boosting”,即极端梯度提升。
-
XGBoost相比于传统的GBM,有以下主要优势:内置的正则化可以防止过拟合;并行计算可以大幅度提高训练速度;内存优化可以处理大规模数据;内置的交叉验证和早停可以方便地选择最佳模型。
-
XGBoost中的正则化项包括对模型的复杂度进行惩罚,如树的深度(叶子节点的数量)和节点分裂的质量(分裂后的增益)。这种正则化可以防止模型过拟合,提高模型的泛化能力。
-
XGBoost中的
learning_rate参数是每个树的权重缩减系数,用于控制每次迭代的步长。较小的learning_rate可以使模型更稳健,但需要更多的迭代次数。 -
XGBoost中的
subsample参数控制每次迭代用于训练的样本比例,colsample_bytree参数控制每次分裂时用于构建树的特征比例。这两个参数可以引入随机性,防止过拟合,提高模型的泛化能力。 -
DMatrix是XGBoost中的一个内部数据结构,用于提高内存效率和训练速度。它可以处理稀疏数据,支持并行和分布式计算。 -
在XGBoost中,
objective='binary:logistic'表示我们正在解决一个二分类问题,并且使用逻辑回归作为单个模型的损失函数。 -
Boosting是一种集成方法,通过串行地训练模型,每次训练的模型都试图修正前一次的错误,从而创建一个强分类器。而Bagging(如随机森林)则是通过并行地训练多个模型,然后通过投票(分类问题)或平均(回归问题)的方式来整合各个模型的预测结果。Boosting主要关注偏差(即模型的准确性),而Bagging主要关注方差(即模型的稳定性)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号