05 线性分类-逻辑斯蒂回归
逻辑斯蒂回归.ipynb
1、逻辑斯蒂回归
1.1、逻辑斯蒂回归是什么
逻辑回归不是一个回归的算法,逻辑回归是一个分类【用于二分类】的算法,好比卡巴斯基不是司机,红烧狮子头没有狮子头一样。
那为什么逻辑回归不叫逻辑分类?因为逻辑回归算法是基于多元线性回归的算法。而正因为此,逻辑回归这个分类算法是线性的分类器。
逻辑回归中对应一条非常重要的S型曲线,对应的函数是Sigmoid函数:
\(f(x) = \frac{1}{1 + e^{-x}}\)
它有一个非常棒的特性,其导数可以用其自身表示:
\(\begin{aligned}f'(x) &= \frac{e^{-x}}{(1 + e^{-x})^2} \\\\&=\frac{1}{1+e^{-x}} * \frac{1 + e^{-x} - 1}{1 + e^{-x}} \\\\&=\frac{1}{1+e^{-x}} * (1- \frac{1}{1+e^{-x}})\\\\&= f(x) * (1 - f(x))\end{aligned}\)
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1 + np.exp(-x))
x = np.linspace(-5,5,100)
y = sigmoid(x)
plt.plot(x,y,color = 'green')

1.2、Sigmoid函数介绍
逻辑回归就是在多元线性回归基础上把结果缩放到 0 ~ 1 之间。 \(h_{\theta}(x)\) 【概率函数,用于分类,分类的目标函数】越接近 1 越是正例,\(h_{\theta}(x)\) 越接近 0 越是负例,根据中间 0.5 将数据分为二类。其中\(h_{\theta}(x)\) 就是概率函数~
\(h_{\theta}(x) = g(\theta^Tx) = \frac{1}{1 + e^{-\theta^Tx}}\)
分类器的本质就是要找到分界,所以当我们把 0.5 作为分类边界时,我们要找的就是 \(\hat{y} = h_{\theta}(x) = \frac{1}{1 + e^{-\theta^Tx}} = 0.5\) ,即 \(z = \theta^Tx = 0\) 时,\(\theta\) 的解~

求解过程如下:

什么事情,都要做到知其然,知其所以然,我们知道二分类有个特点就是正例的概率 + 负例的概率 = 1。一个非常简单的试验是只有两种可能结果的试验,比如正面或反面,成功或失败,有缺陷或没有缺陷,病人康复或未康复等等。为方便起见,记这两个可能的结果为 0 和 1,下面的定义就是建立在这类试验基础之上的。 如果随机变量 x 只取 0 和 1 两个值,并且相应的概率为:
- \(Pr(x = 1) = p; Pr(x = 0) = 1-p; 0 < p < 1\)
则称随机变量 x 服从参数为 p 的Bernoulli伯努利分布( 0-1分布),则 x 的概率函数可写:
- \(f(x | p) = \begin{cases}p^x(1 - p)^{1-x}, &x = 1、0\\0,& x \neq 1、0\end{cases}\)
逻辑回归二分类任务会把正例的 label 设置为 1,负例的 label 设置为 0,对于上面公式就是 x = 0、1。
2、逻辑回归公式推导
2.1、损失函数推导
这里我们依然会用到最大似然估计思想,根据若干已知的 X,y(训练集) 找到一组 \(\theta\) 使得 X 作为已知条件下 y 发生的概率最大。
\(P(y|x;\theta) = \begin{cases}h_{\theta}(x), &y = 1\\1-h_{\theta}(x),& y = 0\end{cases}\)
整合到一起(二分类就两种情况:1、0)得到逻辑回归表达式:
\(P(y|x;\theta) = (h_{\theta}(x))^{y}(1 - h_{\theta}(x))^{1-y}\)
我们假设训练样本相互独立,那么似然函数表达式为:
\(L(\theta) = \prod\limits_{i = 1}^nP(y^{(i)}|x^{(i)};\theta)\)
\(L(\theta) = \prod\limits_{i=1}^n(h_{\theta}(x^{(i)}))^{y^{(i)}}(1 - h_{\theta}(x^{(i)}))^{1-y^{(i)}}\)
对数转换,自然底数为底
\(l(\theta) = \ln{L(\theta)} =\ln( \prod\limits_{i=1}^n({h_{\theta}(x^{(i)}))^{y^{(i)}}}{(1 - h_{\theta}(x^{(i)}))^{1-y^{(i)}}})\)
化简,累乘变累加:
\(l(\theta) = \ln{L(\theta)} = \sum\limits_{i = 1}^n(y^{(i)}\ln(h_{\theta}(x^{(i)})) + (1-y^{(i)})\ln(1-h_{\theta}(x^{(i)})))\)
总结,得到了逻辑回归的表达式,下一步跟线性回归类似,构建似然函数,然后最大似然估计,最终推导出 \(\theta\) 的迭代更新表达式。只不过这里用的不是梯度下降,而是梯度上升,因为这里是最大化似然函数。通常我们一提到损失函数,往往是求最小,这样我们就可以用梯度下降来求解。最终损失函数就是上面公式加负号的形式:
\(J(\theta) = -l(\theta) = -\sum\limits_{i = 1}^n[y^{(i)}\ln(h_{\theta}(x^{(i)})) + (1-y^{(i)})\ln(1-h_{\theta}(x^{(i)}))]\)
2.2、立体化呈现
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.preprocessing import scale # 数据标准化Z-score
# 1、加载乳腺癌数据
data = datasets.load_breast_cancer()
X, y = scale(data['data'][:, :2]), data['target']
# 2、求出两个维度对应的数据在逻辑回归算法下的最优解
lr = LogisticRegression()
lr.fit(X, y)
# 3、分别把两个维度所对应的参数W1和W2取出来
w1 = lr.coef_[0, 0]
w2 = lr.coef_[0, 1]
print(w1, w2)
# 4、已知w1和w2的情况下,传进来数据的X,返回数据的y_predict
def sigmoid(X, w1, w2):
z = w1*X[0] + w2*X[1]
return 1 / (1 + np.exp(-z))
# 5、传入一份已知数据的X,y,如果已知w1和w2的情况下,计算对应这份数据的Loss损失
def loss_function(X, y, w1, w2):
loss = 0
# 遍历数据集中的每一条样本,并且计算每条样本的损失,加到loss身上得到整体的数据集损失
for x_i, y_i in zip(X, y):
# 这是计算一条样本的y_predict,即概率
p = sigmoid(x_i, w1, w2)
loss += -1*y_i*np.log(p)-(1-y_i)*np.log(1-p)
return loss
# 6、参数w1和w2取值空间
w1_space = np.linspace(w1-2, w1+2, 100)
w2_space = np.linspace(w2-2, w2+2, 100)
loss1_ = np.array([loss_function(X, y, i, w2) for i in w1_space])
loss2_ = np.array([loss_function(X, y, w1, i) for i in w2_space])
# 7、数据可视化
fig1 = plt.figure(figsize=(12, 9))
plt.subplot(2, 2, 1)
plt.plot(w1_space, loss1_)
plt.subplot(2, 2, 2)
plt.plot(w2_space, loss2_)
plt.subplot(2, 2, 3)
w1_grid, w2_grid = np.meshgrid(w1_space, w2_space)
loss_grid = loss_function(X, y, w1_grid, w2_grid)
plt.contour(w1_grid, w2_grid, loss_grid,20)
plt.subplot(2, 2, 4)
plt.contourf(w1_grid, w2_grid, loss_grid,20)
# 8、3D立体可视化
fig2 = plt.figure(figsize=(12,6))
ax = Axes3D(fig2)
ax.plot_surface(w1_grid, w2_grid, loss_grid,cmap = 'viridis')
plt.xlabel('w1',fontsize = 20)
plt.ylabel('w2',fontsize = 20)
ax.view_init(30,-30)
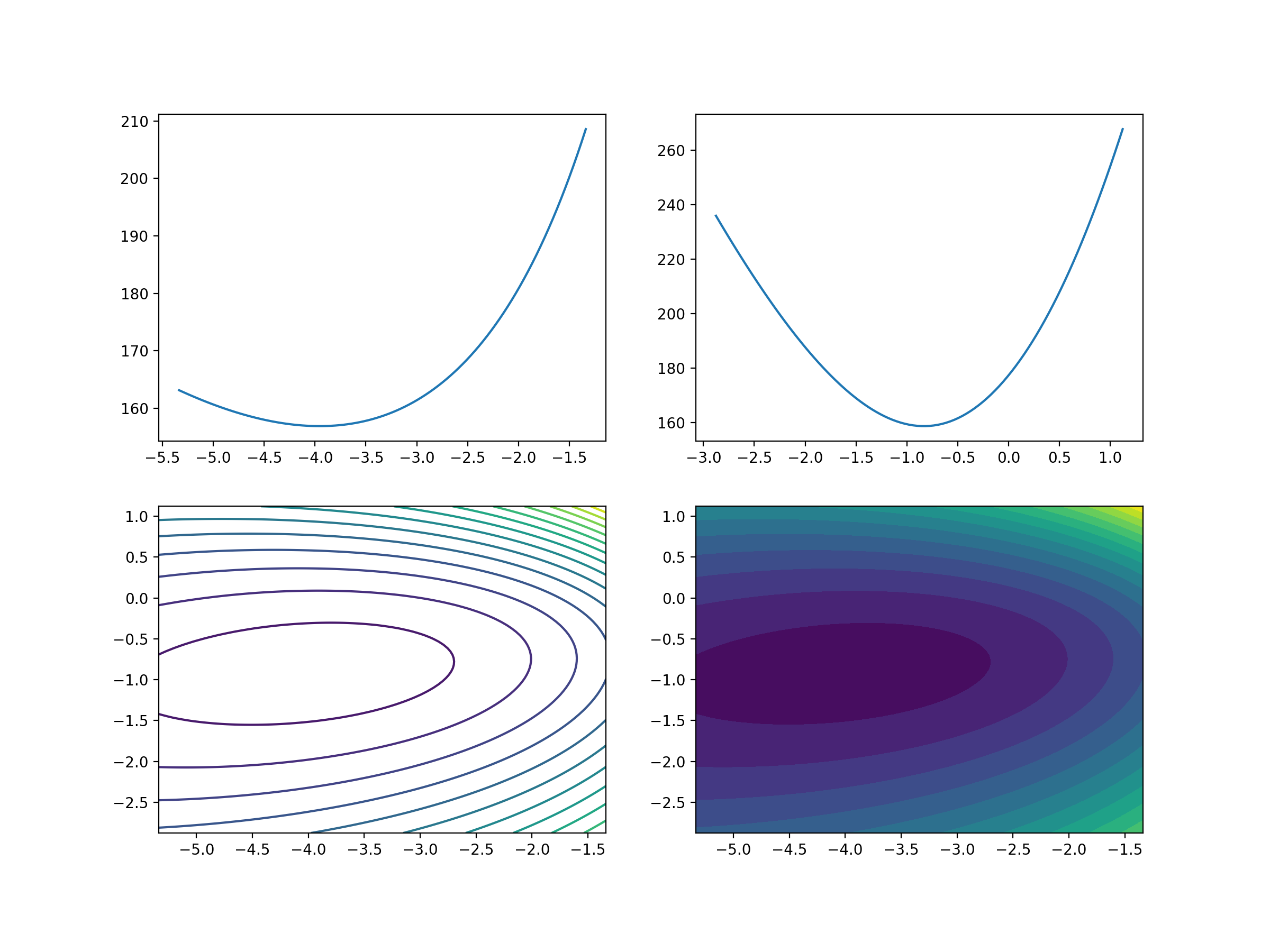

3、逻辑回归迭代公式
3.1、函数特性
逻辑回归参数更新规则和,线性回归一模一样!
\(\theta_j^{t + 1} = \theta_j^t - \alpha\frac{\partial}{\partial_{\theta_j}}J(\theta)\)
- \(\alpha\) 表示学习率
逻辑回归函数:
\(h_{\theta}(x) = g(\theta^Tx) = g(z) = \frac{1}{1 + e^{-z}}\)
- \(z = \theta^Tx\)
逻辑回归函数求导时有一个特性,这个特性将在下面的推导中用到,这个特性为:
\(\begin{aligned} g'(z) &= \frac{\partial}{\partial z}\frac{1}{1 + e^{-z}} \\\\&= \frac{e^{-z}}{(1 + e^{-z})^2}\\\\& = \frac{1}{(1 + e^{-z})^2}\cdot e^{-z}\\\\&=\frac{1}{1 + e^{-z}} \cdot (1 - \frac{1}{1 + e^{-z}})\\\\&=g(z)\cdot (1 - g(z))\end{aligned}\)
回到逻辑回归损失函数求导:
\(J(\theta) = -\sum\limits_{i = 1}^n(y^{(i)}\ln(h_{\theta}(x^{i})) + (1-y^{(i)})\ln(1-h_{\theta}(x^{(i)})))\)
3.2、求导过程
\(\begin{aligned} \frac{\partial}{\partial{\theta_j}}J(\theta) &= -\sum\limits_{i = 1}^n(y^{(i)}\frac{1}{h_{\theta}(x^{(i)})}\frac{\partial}{\partial_{\theta_j}}h_{\theta}(x^{i}) + (1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})}\frac{\partial}{\partial_{\theta_j}}(1-h_{\theta}(x^{(i)}))) \\\\&=-\sum\limits_{i = 1}^n(y^{(i)}\frac{1}{h_{\theta}(x^{(i)})}\frac{\partial}{\partial_{\theta_j}}h_{\theta}(x^{(i)}) - (1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})}\frac{\partial}{\partial_{\theta_j}}h_{\theta}(x^{(i)}))\\\\&=-\sum\limits_{i = 1}^n(y^{(i)}\frac{1}{h_{\theta}(x^{(i)})} - (1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})})\frac{\partial}{\partial_{\theta_j}}h_{\theta}(x^{(i)})\\\\&=-\sum\limits_{i = 1}^n(y^{(i)}\frac{1}{h_{\theta}(x^{(i)})} - (1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})})h_{\theta}(x^{(i)})(1-h_{\theta}(x^{(i)}))\frac{\partial}{\partial_{\theta_j}}\theta^Tx\\\\&=-\sum\limits_{i = 1}^n(y^{(i)}(1-h_{\theta}(x^{(i)})) - (1-y^{(i)})h_{\theta}(x^{(i)}))\frac{\partial}{\partial_{\theta_j}}\theta^Tx\\\\&=-\sum\limits_{i = 1}^n(y^{(i)} - h_{\theta}(x^{(i)}))\frac{\partial}{\partial_{\theta_j}}\theta^Tx\\\\&=\sum\limits_{i = 1}^n(h_{\theta}(x^{(i)}) -y^{(i)})x_j^{(i)}\end{aligned}\)
求导最终的公式:
\(\frac{\partial}{\partial{\theta_j}}J(\theta) = \sum\limits_{i = 1}^n(h_{\theta}(x^{(i)}) -y^{(i)})x_j^{(i)}\)
这里我们发现导函数的形式和多元线性回归一样~
逻辑回归参数迭代更新公式:
\(\theta_j^{t+1} = \theta_j^t - \alpha \cdot \sum\limits_{i=1}^{n}(h_{\theta}(x^{(i)}) -y^{(i)})x_j^{(i)}\)
3.3、代码实战
import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# 1、数据加载
iris = datasets.load_iris()
# 2、数据提取与筛选
X = iris['data']
y = iris['target']
cond = y != 2
X = X[cond]
y = y[cond]
# 3、数据拆分
X_train,X_test,y_train,y_test = train_test_split(X,y)
# 4、模型训练
lr = LogisticRegression()
lr.fit(X_train, y_train)
# 5、模型预测
y_predict = lr.predict(X_test)
print('测试数据保留类别是:',y_test)
print('测试数据算法预测类别是:',y_predict)
print('测试数据算法预测概率是:\n',lr.predict_proba(X_test))
结论:
- 通过数据提取与筛选,创建二分类问题
- 类别的划分,通过概率比较大小完成了
# 线性回归方程
b = lr.intercept_
w = lr.coef_
# 逻辑回归函数
def sigmoid(z):
return 1/(1 + np.exp(-z))
# y = 1 概率
z = X_test.dot(w.T) + b
p_1 = sigmoid(z)
# y = 0 概率
p_0 = 1 - p_1
# 最终结果
p = np.concatenate([p_0,p_1],axis = 1)
p
结论:
- 线性方程,对应方程 \(z\)
- sigmoid函数,将线性方程转变为概率
- 自己求解概率和直接使用LogisticRegression结果一样,可知计算流程正确
4、逻辑回归做多分类
4.1、One-Vs-Rest思想
在上面,我们主要使用逻辑回归解决二分类的问题,那对于多分类的问题,也可以用逻辑回归来解决!
多分类问题:
- 将邮件分为不同类别/标签:工作(y=1),朋友(y=2),家庭(y=3),爱好(y=4)
- 天气分类:晴天(y=1),多云天(y=2),下雨天(y=3),下雪天(y=4)
- 医学图示:没生病(y=1),感冒(y=2),流感(y=3)
- ……
上面都是多分类问题。
假设我们要解决一个分类问题,该分类问题有三个类别,分别用△,□ 和 × 表示,每个实例有两个属性,如果把属性 1 作为 X 轴,属性 2 作为 Y 轴,训练集的分布可以表示为下图:
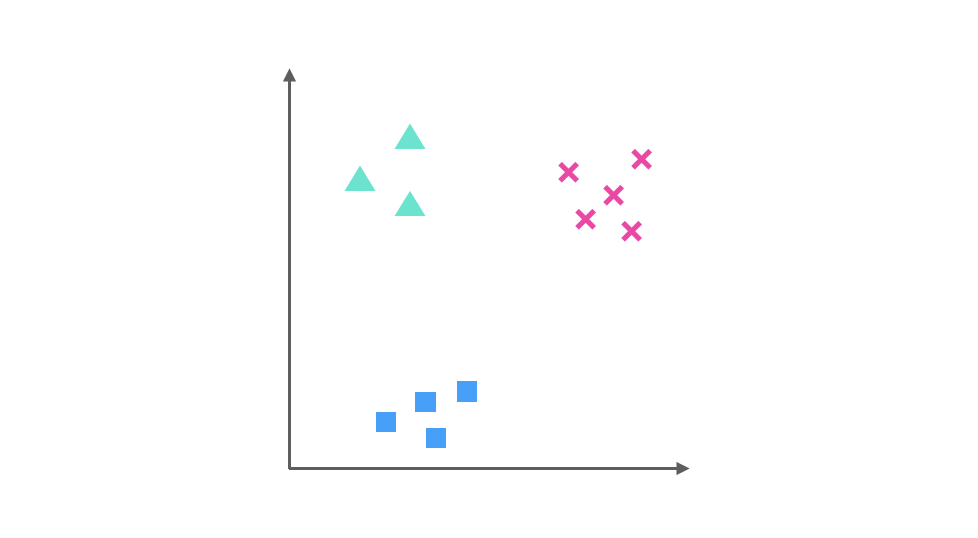
One-Vs-Rest(ovr)的思想是把一个多分类的问题变成多个二分类的问题。转变的思路就如同方法名称描述的那样,选择其中一个类别为正类(Positive),使其他所有类别为负类(Negative)。比如第一步,我们可以将 △所代表的实例全部视为正类,其他实例全部视为负类,得到的分类器如图:

同理我们把 × 视为正类,其他视为负类,可以得到第二个分类器:
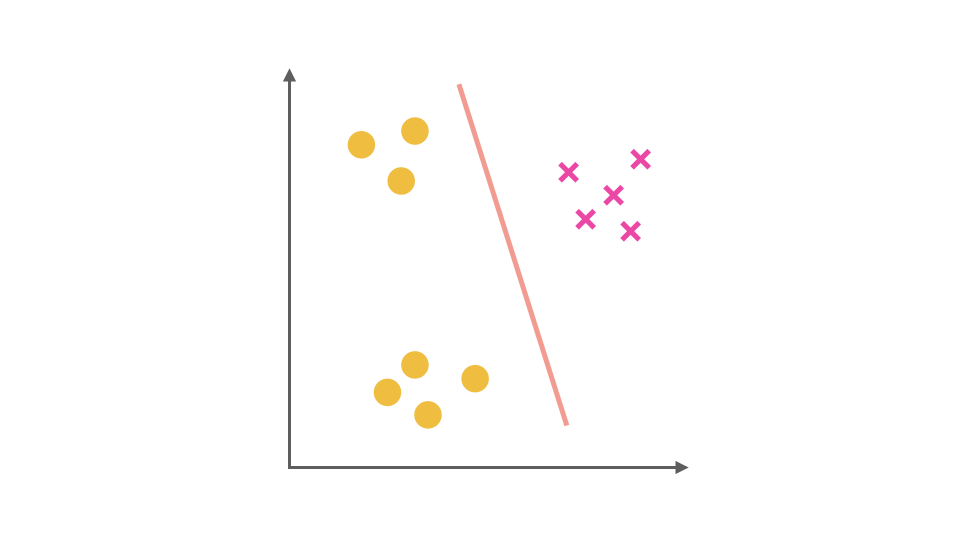
最后,第三个分类器是把 □ 视为正类,其余视为负类:
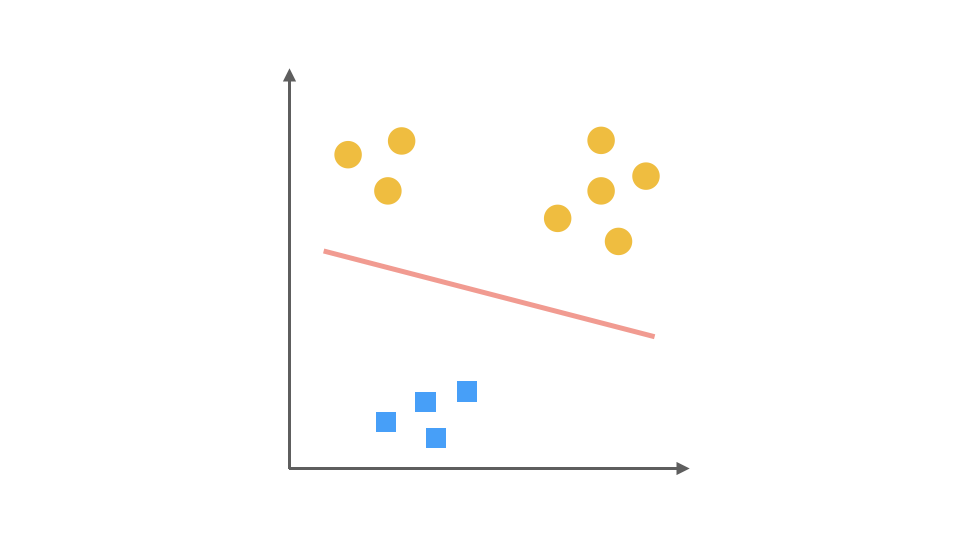
对于一个三分类问题,我们最终得到 3 个二元分类器。在预测阶段,每个分类器可以根据测试样本,得到当前类别的概率。即 P(y = i | x; θ),i = 1, 2, 3。选择计算结果最高的分类器,其所对应类别就可以作为预测结果。
One-Vs-Rest 作为一种常用的二分类拓展方法,其优缺点也十分明显:
- 优点:普适性还比较广,可以应用于能输出值或者概率的分类器,同时效率相对较好,有多少个类别就训练多少个分类器。
- 缺点:很容易造成训练集样本数量的不平衡(Unbalance),尤其在类别较多的情况下,经常容易出现正类样本的数量远远不及负类样本的数量,这样就会造成分类器的偏向性。
4.2、代码实战
import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# 1、数据加载
iris = datasets.load_iris()
# 2、数据提取
X = iris['data']
y = iris['target']
# 3、数据拆分
X_train,X_test,y_train,y_test = train_test_split(X,y)
# 4、模型训练
lr = LogisticRegression(multi_class = 'ovr')
lr.fit(X_train, y_train)
# 5、模型预测
y_predict = lr.predict(X_test)
print('测试数据保留类别是:',y_test)
print('测试数据算法预测类别是:',y_predict)
print('测试数据算法预测概率是:\n',lr.predict_proba(X_test))
结论:
- 通过数据提取,创建三分类问题
- 类别的划分,通过概率比较大小完成了
# 线性回归方程,3个方程
b = lr.intercept_
w = lr.coef_
# 逻辑回归函数
def sigmoid(z):
return 1/(1 + np.exp(-z))
# 计算三个方程的概率
z = X_test.dot(w.T) + b
p = sigmoid(z)
# 标准化处理,概率求和为1
p = p/p.sum(axis = 1).reshape(-1,1)
p
结论:
- 线性方程,对应方程 \(z\) ,此时对应三个方程
- sigmoid函数,将线性方程转变为概率,并进行标准化处理
- 自己求解概率和直接使用LogisticRegression结果一样
5、多分类Softmax回归
5.1、多项分布
Softmax 回归是另一种做多分类的算法。多分类就是多项分布,可以理解为二项分布的扩展。投硬币是二项分布,掷骰子是多项分布。
5.2、Softmax回归概率公式
这个模型被应用到 y = {1, 2, ..., k} 就称作 Softmax回归,是逻辑回归的推广。它的概率函数 \(h_{\theta}(x)\):
$ h_{\theta}(x) = \left{ \begin{aligned} &\frac{e{\theta_1Tx}}{\sum\limits_{j = 1}ke{\theta_j^Tx}} , y = 1\ &\frac{e{\theta_2Tx}}{\sum\limits_{j = 1}ke{\theta_j^Tx}} , y = 2\ &...\&\frac{e{\theta_kTx}}{\sum\limits_{j = 1}ke{\theta_j^Tx}}, y = k \end{aligned} \right.$
举例说明:

代码举例:
import numpy as np
x = np.array([3,1,-3])
def softmax(x):
return np.e**x /np.sum(np.e**x)
softmax(x).round(2)
5.3、代码实战
import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# 1、数据加载
iris = datasets.load_iris()
# 2、数据提取
X = iris['data']
y = iris['target']
# 3、数据拆分
X_train,X_test,y_train,y_test = train_test_split(X,y)
# 4、模型训练,使用multinomial分类器,表示多分类
lr = LogisticRegression(multi_class = 'multinomial',max_iter=5000)
lr.fit(X_train, y_train)
# 5、模型预测
y_predict = lr.predict(X_test)
print('测试数据保留类别是:',y_test)
print('测试数据算法预测类别是:',y_predict)
print('测试数据算法预测概率是:\n',lr.predict_proba(X_test))
结论:
- 通过数据提取,创建三分类问题
- 参数multi_class设置成multinomial表示多分类,使用交叉熵作为损失函数
- 类别的划分,通过概率比较大小完成了
# 线性回归方程,3个方程
b = lr.intercept_
w = lr.coef_
# softmax函数
def softmax(z):
return np.exp(z)/np.exp(z).sum(axis = 1).reshape(-1,1)
# 计算三个方程的概率
z = X_test.dot(w.T) + b
p = softmax(z)
p
结论:
- 线性方程,对应方程 \(z\) ,多分类,此时对应三个方程
- softmax函数,将线性方程转变为概率
- 自己求解概率和直接使用LogisticRegression结果一样


 浙公网安备 33010602011771号
浙公网安备 33010602011771号