平衡二叉树
简介
平衡树(Balance Tree,BT) 指的是,它是一 棵空树或它的左右两颗子树的高度差都小于等于1。常见的符合平衡树的有,B树(多路平衡搜索树)、AVL树(二叉平衡搜索树)等。可以保证查询效率较高。
为什么需要平衡二叉树
在某种极端的情况下,二叉排序树更像是一个单链表,如根据数列{1,2,3,4,5}创建一颗二叉排序树,虽然插入速度没有影响,但是查询速度明显降低,不能发挥BST的优势。
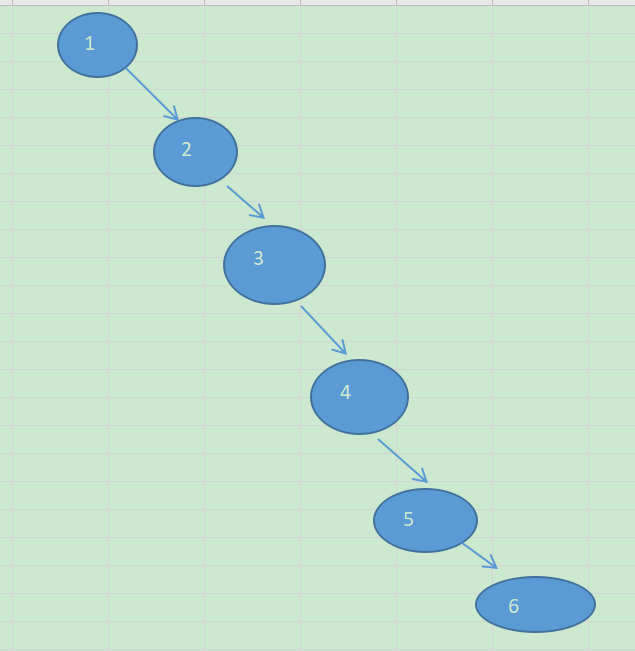
单旋转
左旋转
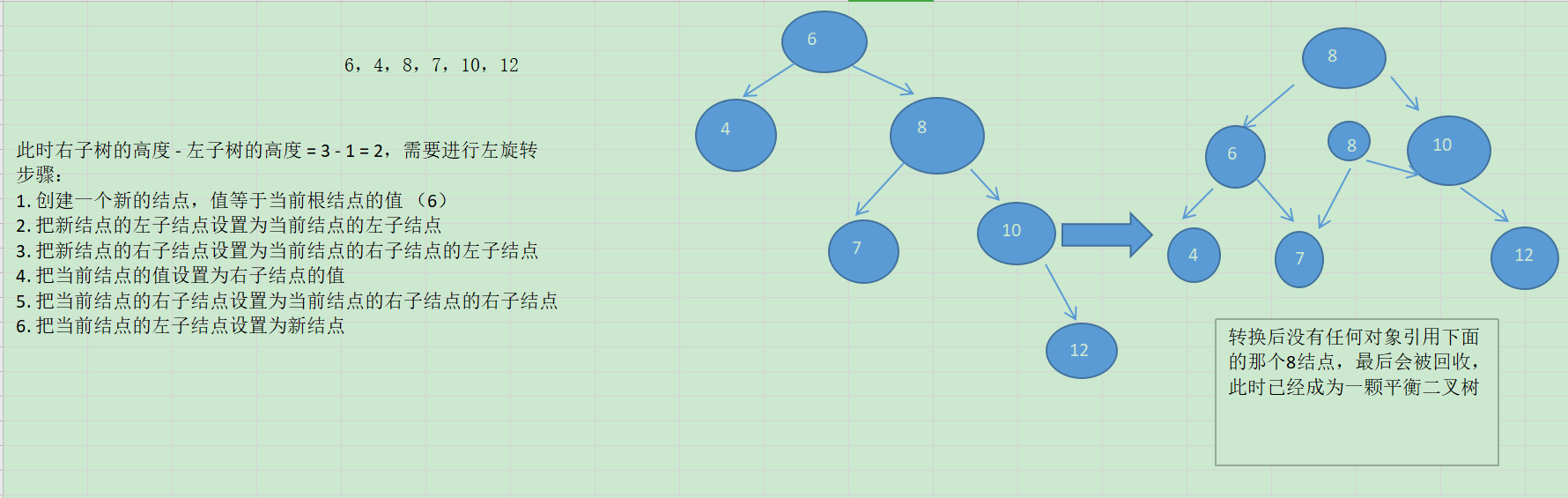
右旋转

双旋转
在某些情况下,单旋转并不能完成平衡二叉树的转换。
- 当符合左旋转的情况下,如果它的左子树的高度大于右子树的高度,先对当前结点的右结点进行右旋转,再对当前结点进行左旋转。
- 如果符合右旋转的情况下,如果它的右子树的高度大于左子树的高度,先对当前结点的左结点进行左旋转,再对当前结点进行右旋转。
代码
class Node {
int value;
Node left;
Node right;
//返回以该结点为根节点的树的高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//返回左子树的高度
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
//返回右子树的高度
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
//左旋转
private void leftRotate() {
//1. 创建新的结点,以当前根结点的值
Node newNode = new Node(value);
//2. 把新的结点的左子结点设置成当前结点的左子结点
newNode.left = left;
//3. 把新的结点的右子结点设置成当前结点的右子结点的左子结点
newNode.right = right.left;
//4. 把当前结点的值替换成右子结点的值
value = right.value;
//5. 把当前结点的右子结点设置成当前结点右子结点的右子结点
right = right.right;
//6. 把当前结点的左子结点设置成新的结点
left = newNode;
}
//右旋转
private void rightRotate() {
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
public Node(int value) {
this.value = value;
}
/**
* 添加结点的方法(二叉排序树)
* @param node 添加的结点
*/
public void add(Node node) {
if (node == null) {
return;
}
if (this.value > node.value) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
} else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
//当添加完一个结点后,如果: (右子树的高度-左子树的高度) > 1 , 左旋转
if (rightHeight() - leftHeight() > 1) {
//如果它的右子树的左子树的高度大于它的右子树的右子树的高度,先对右子结点进行右旋转,然后在对当前结点进行左旋转,否则直接左旋转
if (right != null && right.leftHeight() > right.rightHeight()) {
rightRotate();
}
leftRotate();
return;
}
//当添加完一个结点后,如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
if (leftHeight() - rightHeight() > 1) {
//如果它的左子树的右子树高度大于它的左子树的高度,先对当前结点的左结点(左子树)->左旋转,再对当前结点进行右旋转。否则直接右旋转
if (left != null && left.rightHeight() > leftHeight()) {
leftRotate();
}
rightRotate();
}
}
//中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
//查找要删除的结点
public Node search(int value) {
if (value == this.value) {
return this;
} else if (value < this.value) {
if (this.left == null) {
return null;
}
return this.left.search(value);
} else {
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
//查找要删除的结点的父结点,没找到就返回null
public Node searchParent(int value) {
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
if (value < this.value && this.left != null) {
return this.left.searchParent(value);
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value);
} else {
return null;
}
}
}
}
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
/**
* 添加结点的方法
* @param node 添加的结点
*/
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
//中序遍历
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("二叉树为空,不能遍历");
}
}
//查找要删除的结点
public Node search(int value) {
if (root == null) {
return null;
}
return root.search(value);
}
//查找要删除的结点的父结点
public Node searchParent(int value) {
if (root == null) {
return null;
}
return root.searchParent(value);
}
//删除结点
public void delNode(int value) {
if (root == null) {
return;
}
//得到要删除的结点对象
Node targetNode = search(value);
if (targetNode == null) {
return;
}
//如果满足说明只有一个根结点并且根结点就是要删除的结点
if (root.left == null && root.right == null) {
root = null;
return;
}
//要删除结点的父结点
Node parentNode = searchParent(value);
if (targetNode.left == null && targetNode.right == null) { //叶子结点
if (parentNode.left != null && parentNode.left.value == value) { //判断被删除的结点是不是父结点的左子结点
parentNode.left = null;
} else if (parentNode.right != null && parentNode.right.value == value) { //判断被删除的结点是不是父结点的右子结点
parentNode.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //被删除的节点有两个子结点
targetNode.value = delRightTreeMin(targetNode.right);
} else { //反之只有一个结点
if (targetNode.left != null) {
if (parentNode != null) {
if (parentNode.left != null && parentNode.left.value == value) {
parentNode.left = targetNode.left;
} else {
parentNode.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else {
if (parentNode != null) {
if (parentNode.left != null && parentNode.left.value == value) {
parentNode.left = targetNode.right;
} else {
parentNode.right =targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
/**
* 删除node 为根结点的二叉排序树的最小结点
* @param node 传入的结点
* @return 返回以node为根节点的二叉排序树的最小结点的值
*/
public int delRightTreeMin(Node node) {
Node temp = node;
while (temp.left != null) {
temp = temp.left;
}
delNode(temp.value);
return temp.value;
}
}
测试
int[] arr = { 10, 12, 8, 9, 7, 6};
AVLTree avlTree = new AVLTree();
for (int i : arr) {
avlTree.add(new Node(i));
}
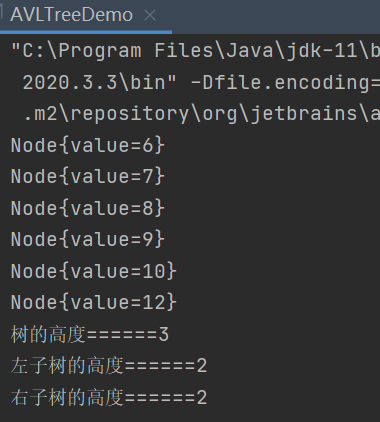
avlTree.infixOrder();
System.out.println("树的高度======" + avlTree.getRoot().height());
System.out.println("左子树的高度======" + avlTree.getRoot().leftHeight());
System.out.println("右子树的高度======" + avlTree.getRoot().rightHeight());




 浙公网安备 33010602011771号
浙公网安备 33010602011771号