堆排序

简介
堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。
每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。
大顶堆示意图

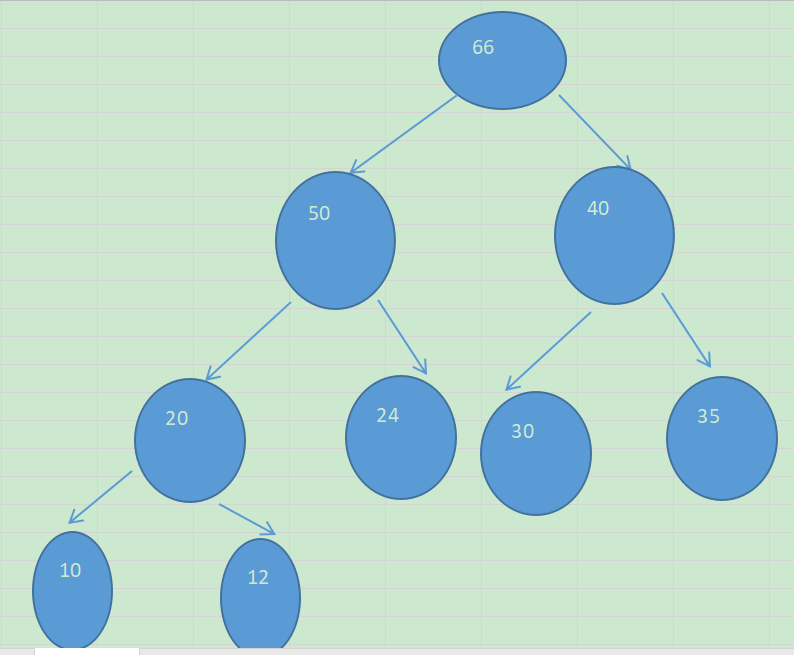
特点：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] //i为结点在数组中的下标
小顶堆示意图

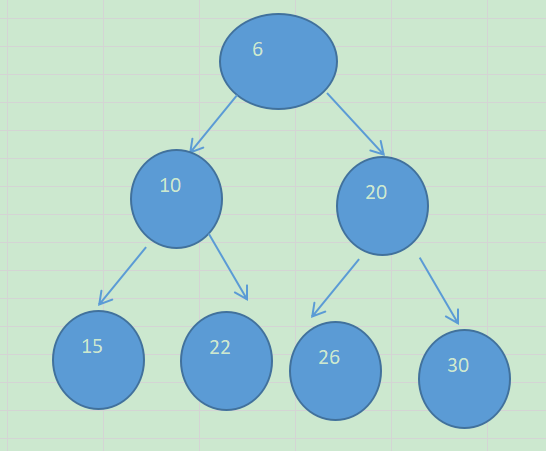
特点：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

一般升序采用大顶堆，降序采用小顶堆 
基本思想

1. 将待排序序列构造成一个大顶堆 （这时堆顶的根节点为序列的最大值）。
2. 将根节点与末尾元素进行交换，此时末尾就为最大值。
3. 然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。
   代码

/**
   * 将 以 i 对应的非叶子结点的树调整成大顶堆
   * @param arr 待调整的数组
   * @param i 非叶子节点在数组中的索引
   * @param length 对多少个元素进行调整，length在逐渐减少
   */
  public static void adjustHeap(int[] arr,int i,int length) {
    int temp = arr[i];
    for (int k = 2 * i + 1;k < length; k = 2 * k + 1) {
      if (k + 1 < length && arr[k] < arr[k + 1]) {
        k++;
      }
      if (arr[k] > temp) {
        arr[i] = arr[k];
        i = k;
      } else {
        break;
      }
    }
    arr[i] = temp;
  }

/**
   * 堆排序
   * arr.length / 2 - 1：非叶子结点在数组中的下标
   * @param arr 排序的数组
   */
  public static void heapSort(int[] arr) {
    int temp;

    for (int i = arr.length / 2 - 1; i >= 0; i--) {
      adjustHeap(arr,i,arr.length);
    }

    for (int j = arr.length - 1; j > 0; j--) {
      temp = arr[j];
      arr[j] = arr[0];
      arr[0] = temp;
      adjustHeap(arr,0,j);
    }
    System.out.println(Arrays.toString(arr));
  }

测试

    int[] arr = {5,3,-1,-12,42,15};
    heapSort(arr);