归并排序

简介
归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

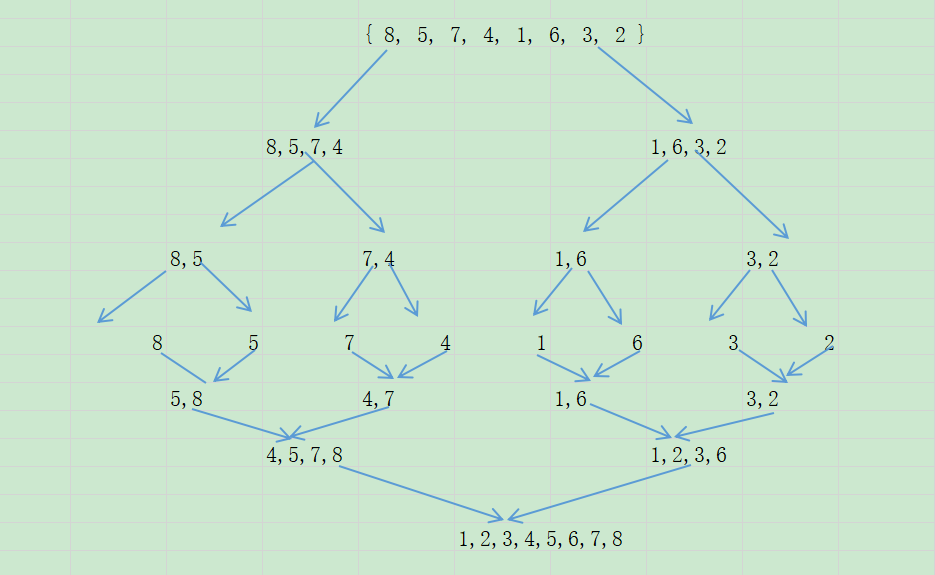
复杂度

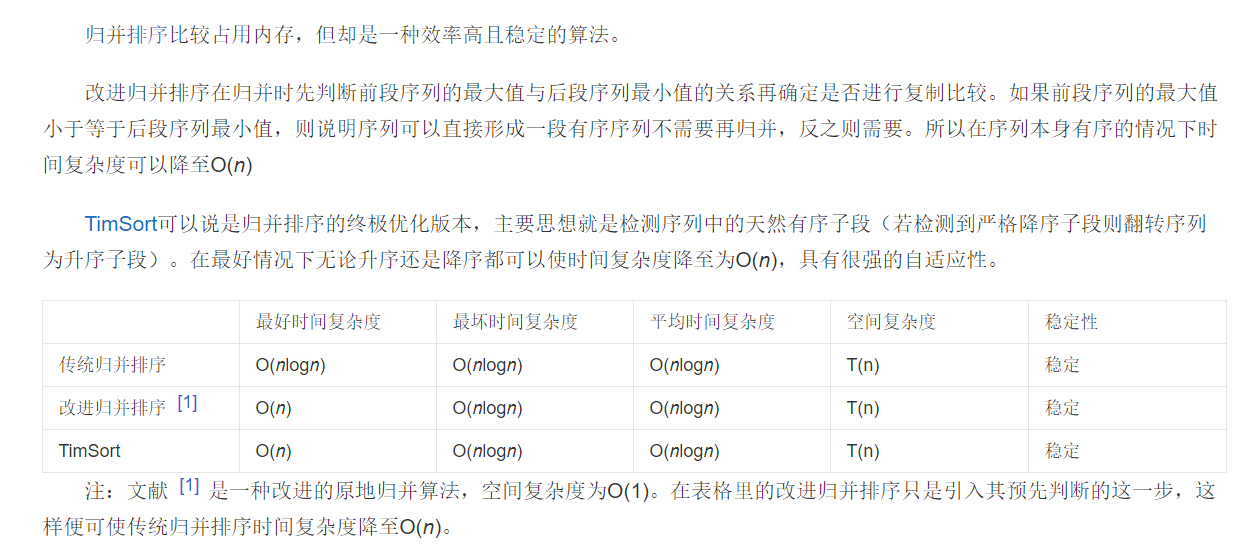
代码

 /**
   * 合并
   * @param arr 操作的数组
   * @param left   左边有序序列的初始索引
   * @param mid 中间索引
   * @param right 右边索引
   * @param temp  中间存储数据的数组
   */
  public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
    int i = left;
    int j = mid + 1;
    int t = 0;
    while (i <= mid && j <= right) {
      if (arr[i] <= arr[j]) {
        temp[t] = arr[i];
        i += 1;
      } else {
        temp[t] = arr[j];
        j += 1;
      }
      t += 1;
    }
    while (i <= mid) {
      temp[t] = arr[i];
      i += 1;
      t += 1;
    }
    while (j <= right) {
      temp[t] = arr[j];
      j += 1;
      t += 1;
    }
    t = 0;
    int tempLeft = left;
    while (tempLeft <= right) {
      arr[tempLeft] = temp[t];
      t += 1;
      tempLeft += 1;
    }
  }

  public static void mergeSort(int[] arr, int left, int right, int[] temp) {
    if (left < right) {
      int mid = (left + right) / 2;
      mergeSort(arr,left,mid,temp);
      mergeSort(arr,mid + 1, right,temp);
      merge(arr,left,mid,right,temp);
    }
  }

测试

    int[] arr = { 8, 5, 7, 4, 1, 6, 3, 2 };
    int[] temp = new int[arr.length];
    mergeSort(arr,0,arr.length - 1,temp);
    System.out.println(Arrays.toString(arr));