数据结构——栈、队列

一、栈以及相关操作

1、定义

        只允许在一端插入和删除的线性表；      

        允许插入和删除的一端称为栈顶(top)，另一端称为栈底(bottom)。

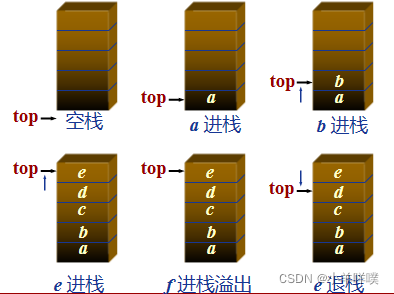
2、特点

        后进先出（LIFO）

3、主要操作

ADT Stack         //对象:由数据类型为StackData的元素构成

{            

        int Push (stack *S, StackData x);    //进栈      

        int Pop (stack *S, StackData &x);     //出栈      

        int GetTop (stack *S, StackData &x); //取栈顶=读栈    ，与出栈的区别就是top是否改变  

        void InitStack (stack *S);         //置空栈 ——make_empty （保留top）    

        int StackEmpty (stack *S);          //判栈空否——出栈必操作      

        int StackFull (stack *S);          //判栈满否 ——进栈必操作

}

（1）栈的数组表示——顺序栈

#define StackSize 100         //定义总长度

typedef char StackData;

typedef struct         //顺序栈定义

{                    

        StackData data[StackSize];              //栈数组    

        int top;                     //栈顶指针

} SeqStack;

初始化        top=-1；

#include <stdio.h>
#include <stdlib.h>

#define SIZE 10
#define MALLOC_OK 1
#define MALLOC_NO 0
#define CREATE_OK 1
#define CREATE_NO 0

enum ret_val{FULL_OK=100,FULL_NO,EMPTY_OK,EMPTY_NO,PUSH_OK,PUSH_NO,POP_OK,POP_NO };	//枚举类型{枚举常量}

//结构体类型，不可以赋值
struct stack_node
{
    int stack_data[SIZE];
    int top;
};		//分号别忘

typedef struct stack_node Stack;
//创建(顺序栈)
void create_stack(Stack ** stack)
{
    *stack = (Stack *)malloc(sizeof(Stack));
}

//初始化top
void init_stack(Stack * stack)
{
    stack->top= -1;
}

//判断是否满栈
int is_full(Stack * stack)
{
    if(stack->top >= SIZE-1)
    {
	return FULL_OK;
    }
    return FULL_NO;
}

//判断是否空栈
int is_empty(Stack * stack)
{
    if(stack->top == -1)
    {
        return EMPTY_OK;
    }
    return EMPTY_NO;
}

//进栈
int push_stack(Stack *stack,int num)
{

    if(FULL_NO == is_full(stack))
    {
/*
        stack->top++;
        stack->stack_data[top]=num;
*/
        stack->stack_data[++stack->top]=num;		//等价于上面
    
        return PUSH_OK;
    }
    printf("stack is full!\n");
    return PUSH_NO;
}

//出栈
int  pop_stack(Stack *stack)
{
    if(EMPTY_NO == is_empty(stack))
    {
	return stack->stack_data[stack->top--];
    }
    return POP_NO;
}

//取栈顶
int gettop_stack(Stack *stack,int num)

//置空栈
void empty_stack(Stack *stack)

int main()
{
    Stack * stack;

    int i;
    int num;
    create_stack(&stack);
    init_stack(stack);

    for(i=0;i<10;i++)
    {
	if(PUSH_OK == push_stack(stack,i+1))
	{
	printf("%4d",i);
	}
	else
	{
	    printf("push stack fail!\n");
	}
    }
	
    printf("\n");
    

    for(i=0;i<10;i++)
    {
	num = pop_stack(stack);

	if(POP_NO != num)
	{
	    printf("%4d",num);
	}
	else
	{
	    printf("pop stack fail!\n");
	}
    }
	printf("\n");
    
   

	free(stack);

    return 0;
}

（2）栈的链接表示——链式栈

优点：

• 链式栈无栈满问题，空间可扩充
• 插入与删除仅在栈顶处执行
• 链式栈的栈顶在链头
• 适合于多栈操作

typedef int StackData;

typedef struct node

{    

        StackData data;           //结点数据        

        struct node * link;           //结点链指针

} StackNode;

typedef struct

{    

        StackNode *top;           //栈顶指针

} LinkStack;

void InitStack ( LinkStack *S )

{    

        S->top = NULL;

}

int Push ( LinkStack *S, StackData x )

{    

        StackNode *p = ( StackNode * ) malloc( sizeof ( StackNode ) );    

        p->data = x;  

        p->link = S->top;    

        S->top = p;  

        return 1;

}

int StackEmpty (LinkStack *S)

{    

        return S->top == NULL;

}

int Pop ( LinkStack *S, StackData &x )

{    

        if ( StackEmpty (S) )

        return 0;    

        StackNode * p = S->top;    

        S->top = p->link;    

        x = p->data;    

        free (p);    

        return 1;

}  

  int GetTop ( LinkStack *S, StackData &x )

{    

        if ( StackEmpty (S) )

        return 0;    

        x = S->top->data;    

        return 1;

}

4、应用

        建立操作数栈和运算符栈。

5、运算符规则

• 自左至右扫描表达式，凡是遇到操作数一律进操作数栈。
• 当遇到运算符时，如果它的优先级比运算符栈栈顶元素的优先级高就进栈。反之，取出栈顶运算符和操作数栈栈顶的连续两个操作数进行运算，并将结果存入操作数栈，然后继续比较该运算符与栈顶运算符的优先级。
• 左括号一律进运算符栈，右括号一律不进运算符栈，取出运算符栈顶运算符和操作数栈顶的两个操作数进行运算，并将结果压入操作数栈，直到取出左括号为止。

二、队列以及相关操作