从NMS谈起——实时ANMS

上一篇中讲到ANMS可以实现关键点在局部上的稀疏分布和全局上的均匀分布。然而由于时间复杂度太高，无法实时运行，因此不具备实用价值。

Approximate ANMS

为解决这一问题，学术界通过近似，提出了能够实时运行同时效果接近于ANMS的算法。这里对Efficient adaptive non-maximal suppression algorithms for homogeneous spatial keypoint distribution 中提出的SSC算法进行介绍

Suppression via Square Covering(SSC)

不同于ANMS算法直接算出每个点的最大响应距离，然后通过排序拿出指定的n个关键点。 SSC算法利用图像存储在空间上的离散性来加速这一过程。
它的基本流程如下图所示。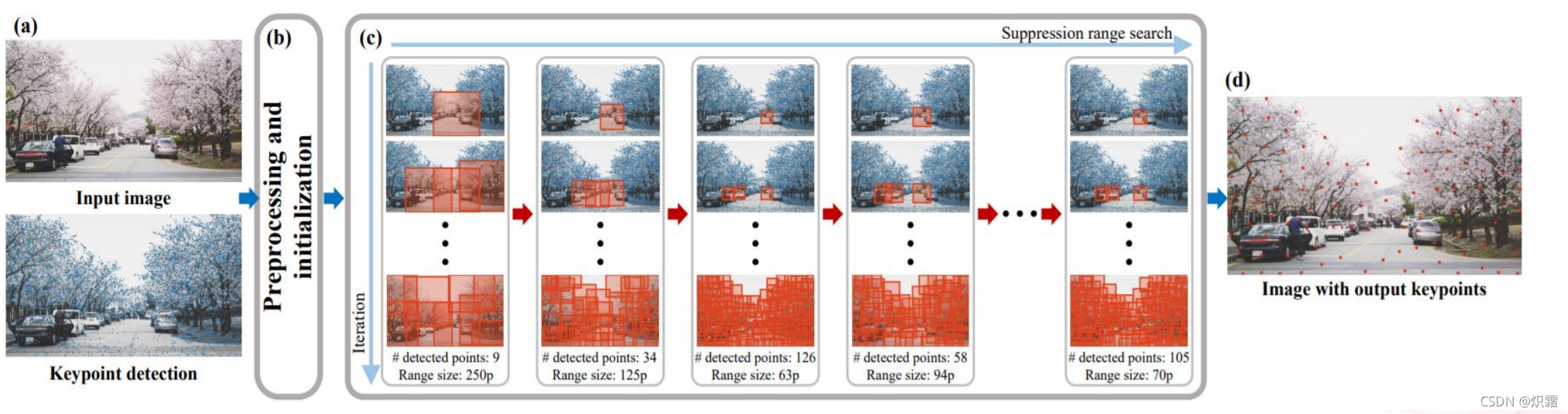
如图，SSC算法是一个迭代选取关键点以及试错逼近给定数量的过程。它的基本思想是先猜测一个响应距离d，然后以此为依据，依照响应度从大到小，拿出响应度最高且彼此相隔至少为d的m个关键点。通过使用与图像等大的mask，这里可以将时间复杂度降低为常数级。显然这m个关键点必然满足

$$r_i=min||x_i-x_j||,s.t.response(x_i)<response(x_j),x_j\in S$$

即在范围d的区域中它的响应度最高。如果m<n，则缩小d到原来的1/2，再进行一次上面的过程。如果m>n，则增大d。这一过程是一个二分查找的过程。当$|m-n|<k$时，则停止这个流程，k为设置的误差阈值。此时输出的关键点满足ANMS算法的条件。

实际使用的过程中，往往只需要5~8次迭代就可以达到目标，1000个点在PC上耗时不到1ms。当然，实际上由于取关键点的过程中，计算距离并非严格使用欧式距离，SSC算法最终得到的点与ANMS有一些细微的不同。

代码及其他

SSC算法发表于2018年，代码可以在https://github.com/BAILOOL/ANMS-Codes找到，作者将其应用于SLAM中，获得了一定程度的提升。
另一方面SLAM是一个各个模块耦合较深的系统，传统的ORB-SLAM Bucketing方法已经深入人心，并且与它的模块互相作用，导致很难正确的评估和推广新的关键点分布算法了。

Reference

Bailo O, Rameau F, Joo K, et al. Efficient adaptive non-maximal suppression algorithms for homogeneous spatial keypoint distribution[J]. Pattern Recognition Letters, 2018, 106: 53-60.