【氵】论如何在算法竞赛中用python乱艹偏题怪题

【氵】论如何在算法竞赛中用 python 乱艹偏题怪题

虽然说 python 本身由于执行效率的问题，大多数情况下，在算法竞赛中并不是那么常见。不过在某些偏题怪题中，python 或许能起到一些逃课的作用。

例1 —— 2025 GPLT 天梯赛 —— L2 算式拆解

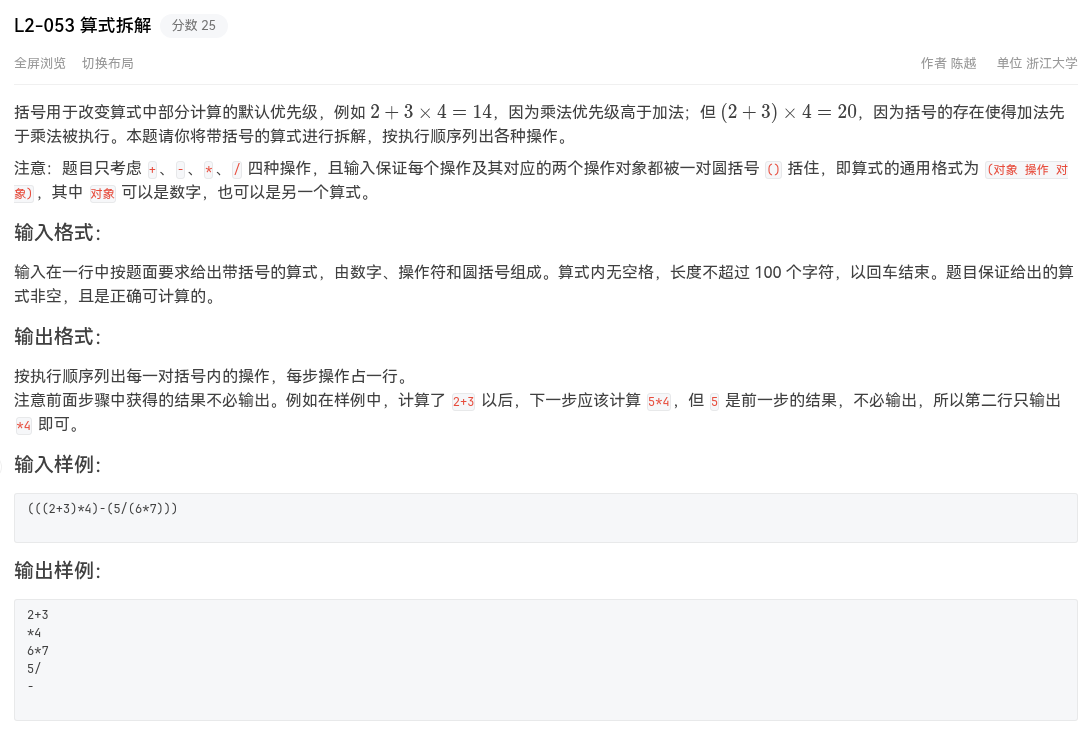
题目大意是给定一个由括号、加、减、乘、除和数字组成的表达式，你需要按照顺序输出这个表达式的计算过程。

比如 (((2+3)*4)-(5/(6*7))) 这个算式，你需要输出的答案就是：

2+3
*4
6*7
5/
-

特别的，如果某一步计算中，用到的某个数字是以前步骤计算出来的结果，那么我们应当略过这个数字。

例如在样例中，计算了 2+3 以后，下一步应该计算 5*4，但 5 是前一步的结果，不必输出，所以第二行只输出 *4。

常规的写法应该是写一个 parser 一类的东西进行解析。

但是，如果你就是不想去写这个 parser，怎么办？

办法其实是有的。我们知道 python 的 eval 以及 exec 这两个函数都有自动帮你解析并运算一个复杂表达式的功能。

但是，直接对输入的表达式调用 eval 的话，它直接就给算完了！而我们所需要的，是计算过程的中间步骤。

那怎么办呢？

一种方式是，用一个自己实现的类（比如这里叫做 Tmp）把所有的数字包一下，定义好 Tmp 类的 +-*/ 四种运算，然后在负责运算的函数内输出这个过程即可。

总结一下步骤：

1. 定义 Tmp 类，为其实现 +-*/ 的方法。
2. 读取输入，用 re（python 的正则表达式库）将所有的 \d+ 周围包上 Tmp()。
3. 调用 eval（或者是 exec）进行计算。

代码如下：

import re


class Tmp:
    __slots__ = ["name"]

    def __init__(self, x):
        self.name = f'{x}'

    @staticmethod
    def print(a, b, c):
        print(a.name + c + b.name)

    def __add__(self, oth):
        __class__.print(self, oth, "+")
        return Tmp("")

    def __sub__(self, oth):
        __class__.print(self, oth, "-")
        return Tmp("")

    def __mul__(self, oth):
        __class__.print(self, oth, "*")
        return Tmp("")

    def __truediv__(self, oth):
        __class__.print(self, oth, "/")
        return Tmp("")


if __name__ == "__main__":
    eval(re.sub(r"(\d+)", r"Tmp(\1)", input()))

写起来特别简单。

• __init__ 函数中 f'{x}' 是为了将 x 强转成字符串。
• __add__、__sub__、__mul__、__truediv__ 分别是加法、减法、乘法、普通除法（也就是一个左斜杠的除法，两个左斜杠的整除叫做 __floordiv__）。
• r"(\d+)" 表示匹配长度大于等于 \(1\) 的整数，并捕获为第一个捕获组。r"Tmp(\1)" 中，\1 就是去获取编号为 \(1\) 的捕获组。

之后再看下一个例子：

例2 —— 2023 ICPC 西安 —— Problem N. Python Program

题目大意是，输入一个形如下面这样的 python 程序，你需要输出它的运算结果。

ans=0
for q in range(100,50,-1):
    for i in range(q,77,20):
        ans+=i
print(ans)

for i in range(a, b, c) 的意思是，\(i\) 从 \(a\) 开始，每次加上 \(c\)，直到离开 \(\left [a, b \right )\)（当 \(c > 0\) 时）或者是 \(\left (b, a \right]\)（当 \(c < 0\) 时）这一范围。

数据范围保证 range 的步长不为 \(0\) 且所有数字的绝对值不超过 \(10^6\)。

直接调用 exec 去进行计算的话（按理来讲）是过不了的。因为两层循环都可能各自循环 \(10^6\) 次，这样总的运算次数就是 \(10^{12}\)，显然运算量太大。

因此考虑优化掉内层的 for 循环。

不难发现这其实就是一个等差数列求和公式。

因此我们可以考虑，用一个自己定义的类型（比如这里叫 MyRange）替换掉内层 for 循环中的那个 range，在迭代时，它会直接返回整个等差数列的和，从而把内层 for 循环优化为 \(O(1)\) 计算。

class MyRange:

    __slots__ = ["val"]

    def __init__(self, a: int, b: int, c: int = 1) -> None:
        if c > 0:
            l: int = (b - a + c - 1) // c if a < b else 0
        else:
            l: int = (a - b - c - 1) // (-c) if a > b else 0
        self.val = (2 * a + (l - 1) * c) * l // 2

    def __iter__(self):
        return [self.val].__iter__()


if __name__ == "__main__":
    source = "\n".join([
        input(),
        input(),
        input().replace("range", "MyRange"),
        input(),
        input(),
    ])

    exec(source)

实现起来也是相当的简单。

• python 的迭代需要你的类型实现一个 __iter__ 方法。假设这个实例叫做 a。当调用 a.__iter__() 的时候，它需要返回一个具有 __next__ 方法的实例 b。每次调用 b.__next__() 的时候：若迭代还没结束，它会返回当前迭代到的值；否则，它需要抛出 StopIteration 这个异常。
• 不过这其实是无关紧要的，因为你可以在 __iter__ 方法中直接返回一个 list 的迭代器，帮你完成这一过程（上面代码中的 return [self.val].__iter__() 其实干的就是这个事情）。