CF56E题解
原题
思路概述
题意分析
给定一个坐标轴上 \(n\) 个骨牌,每个骨牌分别有坐标与高度 \(x_i,h_i\)。求推倒每个骨牌后能倒下的骨牌数目。
思路分析
初步阅读题目,认为是简单挂链+倍增题目,即每个骨牌的唯一后继是其倒下后能覆盖到的最远骨牌,直接处理倍增数组即可求解。但在几次试错后,笔者发现一种特殊状态:即选择覆盖到的最远骨牌不一定是实际覆盖方案。比如在下图中,在考虑骨牌 \(AB\) 时,若找到其能覆盖的最远骨牌 \(EF\) ,那么推倒骨牌 \(AB\) 只会有三个骨牌倒下,但实际结果是四个骨牌都会倒下。
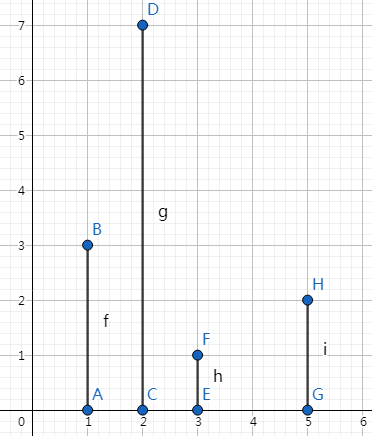
因此,对于一个骨牌,不能简单将其覆盖区间内最远的骨牌作为其后继。
一个骨牌倒下时,其覆盖区间内的所有骨牌都会全部倒下。但若对区间内的所有骨牌全部进行,时间复杂度就变为了 \(O(n^2)\) ,不能适应本题数据规模。而进一步观察后不难发现,区间内的所有骨牌中,对最后结果贡献最大的始终是倒下后覆盖区间右端点最大的(以上图为例,推倒骨牌 \(AB\) 后,真正决定最后倒下骨牌数量的是覆盖区间右端点为 \((9,0)\) 的骨牌 \(CD\) )。因此,只需要在当前考虑骨牌范围内找出右端点(即 \(x_i+h_i\) )最大的骨牌作为其后继,再用挂链+倍增处理即可。
算法实现
关于覆盖区间的处理
显然可以看出,对于当前选中的骨牌倒下后能覆盖到的其他骨牌,若采用循环枚举的策略,其时间复杂度仍然是 \(O(n^2)\) 的。此处直接使用二分查找,对于骨牌 \(i\) 找到最大的 \(j\) 满足 \(x_j<x_i+h_i\) 即为能覆盖到的最远骨牌。
关于后继的查询
本题题解区已经有DP做法。但笔者在此处提供ST表+二分查找的做法。但所有的做法都需要将骨牌按坐标排序。
由于ST表有静态区间最值查询功能,所以我们将排序后的每个骨牌倒下后能覆盖到的最右端点 \(x_i+h_i\) 作为查询元素求最大值。再在区间内用二分找到当前考虑骨牌的后继(后继定义如上文所述)。具体算法流程如下(设当前骨牌下标为 \(pos\) ,二分区间为 \([pos+1,n]\)):
\(\text{while}(l<r)\)
\(\{\)
\(\text{define}\) \(mid=\frac{l+r}{2}\)
\(\text{if}\) \((ST\_query(l,mid)<ST\_query(mid+1,r))\) \(\text{do}\) \(l=mid+1\)
\(\text{otherwise}\) \(r=mid\)
\(\}\)
倍增数组的处理
倍增数列的用法与一般倍增题一致,转移方程为:
统计答案时不再采用ans+=1<<i的形式,而是直接加上倍增数组上移动前后的下标代数差。
AC code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<set>
#include<ctime>
#define RI register int
using namespace std;
const int maxn=1e5+10,maxlog=20;
typedef struct
{
int x,h,ord;
int nex[maxlog+1];
inline int clac(void){return x+h;}/*求当前骨牌覆盖区间右端点*/
}card;
card a[maxn];
int n;
int f[maxn][maxlog+1],lg[maxn]/*ST表查询区间内骨牌能覆盖区间右端点最大值*/,ans[maxn];
inline bool cmp(card x,card y);/*按坐标给骨牌排序*/
inline int bsr(int l,int r,int x);/*二分查找当前骨牌能覆盖到的最远的骨牌*/
inline void init(int x);/*输入与ST表初始化*/
inline int query(int l,int r);/*各骨牌覆盖区间右端点最大值查询*/
inline int gmx(int l,int r);/*二分查找区间内覆盖区间右端点最大的骨牌*/
int main()
{
scanf("%d",&n);init(n);
for(RI i=0;i<=maxlog;++i)/*处理倍增数组*/
for(RI j=1;j<=n;++j)
if(!i) a[j].nex[i]=gmx(j+1,bsr(j+1,n,a[j].clac()));/*求覆盖区间内覆盖区间右端点最大的骨牌*/
else a[j].nex[i]=a[a[j].nex[i-1]].nex[i-1];
for(RI i=1,st=i;i<=n;++i,st=i)
for(RI j=maxlog;j>=0;--j)
if(a[st].nex[j] && a[st].nex[j]<=n)
{
ans[a[i].ord]+=a[st].nex[j]-st;/*st能覆盖到a[st].nex[j],其中间的骨牌都计入st覆盖数量内*/
st=a[st].nex[j];
}
for(RI i=1;i<=n;++i) printf("%d ",ans[i]+1);/*骨牌推倒时自身也会倒下 故答案加一*/
return 0;
}
inline bool cmp(card x,card y)
{
return x.x<y.x;
}
inline int bsr(int l,int r,int x)
{
while(l<r)
{
RI mid=(l+r+1)>>1;
if(x>a[mid].x) l=mid;
else r=mid-1;
}
return (x>a[l].x && l<=n)?l:0;
}
inline void init(int x)
{
/*读入和排序*/
for(RI i=1;i<=x;++i)
{
scanf("%d%d",&a[i].x,&a[i].h);
a[i].ord=i;
}
/*注意 由于答案要求按原顺序输出 所以此处应记录原下标*/
sort(a+1,a+x+1,cmp);
/*初始化ST表*/
for(RI i=1;i<=x;++i) f[i][0]=a[i].clac();
for(RI i=1;(1<<i)<=x;++i)
for(RI j=1;j+(1<<i)-1<=x;++j)
f[j][i]=max(f[j][i-1],f[j+(1<<(i-1))][i-1]);
for(RI i=2;i<=x;++i) lg[i]=lg[i>>1]+1;
return;
}
inline int query(int l,int r)
{
return max(f[l][lg[r-l+1]],f[r-(1<<lg[r-l+1])+1][lg[r-l+1]]);
}
inline int gmx(int l,int r)
{
if(l>r) return 0;/*若此骨牌不能覆盖任何其他骨牌会出现l>r的情况*/
else
{
while(l<r)
{
RI mid=(l+r)>>1;
if(query(l,mid)<query(mid+1,r)) l=mid+1;
else r=mid;
}
return (l<=n)?l:0;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号