05数据结构——树与二叉树
5.2.2二叉树的存储结构
1.顺序存储结构
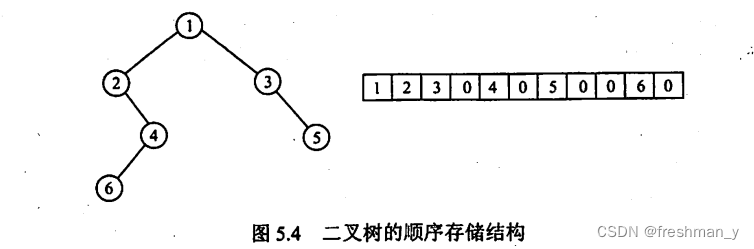
2.链式存储结构 ![]()
二叉树的链式存储结构描述:
typedef struct BiTNode{
ElemType data; //数据域
struct BiTNode *lchild,*rchild; //左、右孩子指针
}BiTNode,*BiTree;5.3.1二叉树的遍历
1.先序遍历(根左右)
void PreOrder(BiTree T){
if(T!=NULL){
visit(T); //访问根结点
PreOrder(T->lchild); //递归遍历左子树
PreOrder(R->rchild); //递归遍历右子树
}
}2.中序遍历(左根右)
void InOrder(BiTree T){
if(T!=NULL){
InOrder(T->lchild); //递归遍历左子树
visit(T); //访问根结点
InOrder(T->rchild); //递归遍历右子树
}
}3.后序遍历(左右根)
void PostOrder(BiTree T){
if(T!=NULL){
PostOrder(T->lchild); //递归遍历左子树
PostOrder(T->rchild); //递归遍历右子树
visit(T); //访问根结点
}
}4.递归算法和非递归算法的转换

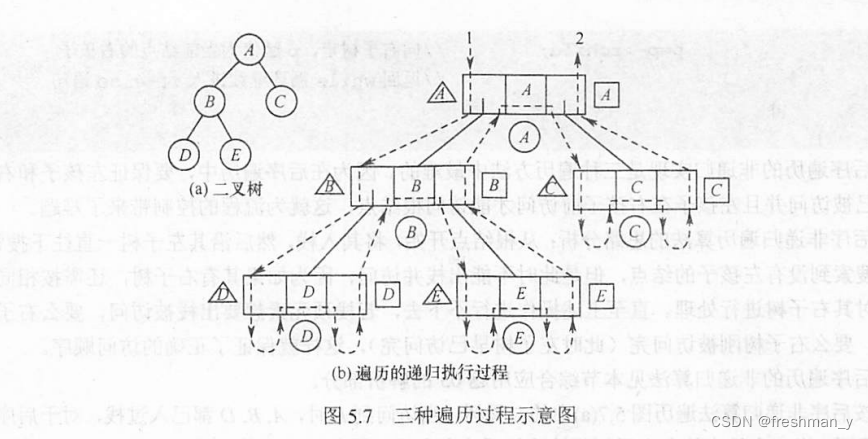
(1).中序遍历的非递归算法如下:
void InOrder2(BiTree T){
InitStack(S); BiTree p=T; //初始化栈S;p是遍历指针
while(p||!IsEmpty(S)){ //栈不空或p不空时循环
if(p){ //一路向左
Push(S,p); //当前结点入栈
p=p->lchild; //左孩子不空,一直向左走
}
else{ //出栈,并转向出栈结点的右子树
Pop(S,p); visit(p); //栈顶元素出栈,访问出栈结点
p=->rchild; //向右子树走,p赋值为当前结点的右孩子
} //返回while循环继续进入if-else语句
}
}(2).先序遍历的非递归算法如下:
void PreOrder2(BiTree T){
InitStack(S); BiTree p=T; //初始化栈S;p是遍历指针
while(p||!IsEmpty(S)){ //栈不空或p不空时循环
if(p){ //一路向左
visit(p);Push(S,p); //访问当前结点,并入栈
p=p->lchild; //左孩子不空,一直向左走
}
else{ //出栈,并转向出栈结点的右子树
Pop(S,p); //栈顶元素出栈
p=p->rchild; //向右子树走,p赋值为当前结点的右孩子
} //返回while循环继续进入if-else语句
}
}(3).后序遍历的非递归算法如下:
void PostOrder3(BiTree T){
InitStack(S);
BiTNode *p=T;
BiTNode *r=NULL;
while(p||!IsEmpty(S)){
if(p){ //走到最左边
push(S,p);
p=p->lchild;
}
else{ //向右
GetTop(S,p); //读栈顶结点(非出栈)
if(p->rchild&&p->rchild!=r) //若右子树存在,且未被访问过
p=p->rchild; //转向右
else{ //否则,弹出结点并访问
pop(S,p); //将结点弹出
visit(p->data); //访问该结点
r=p; //记录最近访问过的结点
p=NULL; //结点访问完后,重置p指针
}
}//else
}//while
}5.层次遍历

二叉树的层次遍历算法如下:
void LevelOrder(BiTree T){
InitQueue(Q); //初始化辅助队列
BiTree p;
EnQueue(Q,T); //将根结点入队
while(!IsEmpty(Q)){ //队列不空则循环
DeQueue(Q,p); //队头结点出队
visit(p); //访问出队结点
if(p->lchild!=NULL)
EnQueue(Q,p->lchild); //左子树不空,则左子树根结点入队
if(p->rchild!=NULL)
EnQueue(Q,p->rchild); //右子树不空,则右子树根结点入队
}
}5.3.2线索二叉树
1.线索二叉树的基本概念

线索二叉树的存储结构描述:
typedef struct ThreadNode{
ElemType data; //数据元素
struct ThreadNode *lchild,*rchild; //左、右孩子指针
int ltag,rtag; //左、右线索标志
}ThreadNode,*ThreadTree;2.中序线索二叉树的构造
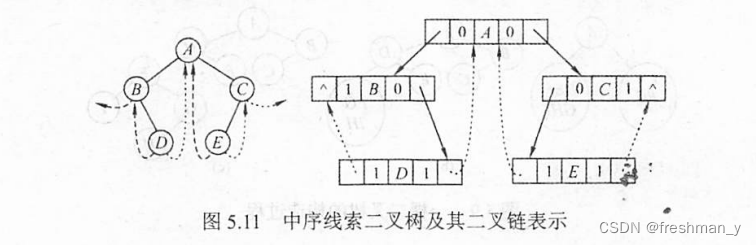
通过中序遍历对二叉树线索化的递归算法如下:
void InThread(ThreadTree &p,ThreadTree &pre){
if(p!=NULL){
InThread(p->lchild,pre); //递归,线索化左子树
if(p->lchild==NULL){ //左子树为空,建立前驱线索
p->lchild=pre;
p->ltag=1;
}
if(pre!=NULL&&pre->rchild==NULL){
pre->rchild=p; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=p; //标记当前结点成为刚刚访问过的结点
InThread(p->rchild,pre); //递归,线索化右子树
}//if(p!=NULL)
} 通过中序遍历建立中序线索二叉树的主要过程算法如下:
void CreateInThread(ThreadTree T){
ThreadTree pre=NULL;
if(T!=NULL){ //非空二叉树,线索化
InThread(T,pre); //线索化二叉树
pre->rchild=NULL; //处理遍历的最后一个结点
pre->rtag=1;
}
}3.先序线索二叉树的构造
通过先序遍历对二叉树线索化的递归算法如下:
void PreThread(ThreadTree &p,ThreadTree &pre){
if(p!=NULL){
if(p->lchild==NULL){ //左子树为空,建立前驱线索
p->lchild=pre;
p->ltag=1;
}
if(pre!=NULL&&pre->rchild==NULL){
pre->rchild=p; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=p;
if(p->ltag==0){ //lchild不是前驱线索
PreThread(p->lchild,pre); //递归,线索化左子树
}
PreThread(p->rchild,pre); //递归,线索化右子树
}
} 通过先序遍历建立中序线索二叉树的主要过程算法如下:
void CreatePreThread(ThreadTree T){
ThreadTree pre=NULL;
if(T!=NULL){ //非空二叉树,线索化
PreThread(T,pre); //线索化二叉树
pre->rchild=NULL; //处理遍历的最后一个结点
pre->rtag=1;
}
}4.后序线索二叉树的构造
通过后序遍历对二叉树线索化的递归算法如下:
void PostThread(ThreadTree &p,ThreadTree &pre){
if(p!=NULL){
PostThread(p->lchild,pre); //递归,线索化左子树
PostThread(p->rchild,pre); //递归,线索化右子树
if(p->lchild==NULL){ //左子树为空,建立前驱线索
p->lchild=pre;
pre->ltag=1;
}
if(pre!=NULL&&pre->rchild==NULL){
pre->rchild=p; //建立前驱结点的后继线索
pre->rtag=p;
}
pre=p;
}
} 通过后序遍历建立中序线索二叉树的主要过程算法如下:
void CreatePostThread(ThreadTree T){
ThreadTree pre=NULL;
if(T!=NULL){
PostThread(T,pre);
pre->rchild=NULL;
pre->rtag=1;
}
}6.中序线索二叉树顺向中序遍历
1)求中序线索二叉树中中序序列下的第一个结点:
ThreadNode *Firstnode(ThreadNode *p){
while(p->ltag==0) p=p->lchild; //最左下结点(不一定是叶结点)
return p;
}2)求中序线索二叉树中结点p在中序序列下的后继:
ThreadNode *Nextnode(ThreadNode *p){
if(p->rtag==0)
return Firstnode(p->rchild);
else
return p->rchild; //rtag==1 直接返回后继线索
}3)利用上面两个算法,可以写出不含头结点的中序线索二叉树的中序遍历算法:
void Inorder(ThreadNode *T){
for(ThreadNode *p=Firstnode(T);p!=NULL;p=Nextnode(p))
visit(p);
}7.中序线索二叉树逆向中序遍历
1)求中序线索二叉树中中序序列下的最后一个结点:
ThreadNode *Lastnode(ThreadNode *p){
while(p->rtag==0) p=p->rchild; //最右下结点(不一定是叶结点)
return p;
}
2)求中序线索二叉树中结点p在中序序列下的前驱:
ThreadNode *Prenode(ThreadNode *p){
if(p->ltag==0)
return Lastnode(p->lchild);
else
return p->lchild; //ltag==1直接访问前驱线索
}3)利用上面两个算法,可以写出不含头结点的中序线索二叉树的逆向中序遍历算法:
void RevInorder(ThreadNode *T){
for(ThreadNode *p=Lastnode(T);p!=NULL;p=Prenode(p))
visit(p);
}5.4.1树的存储结构
1.双亲表示法
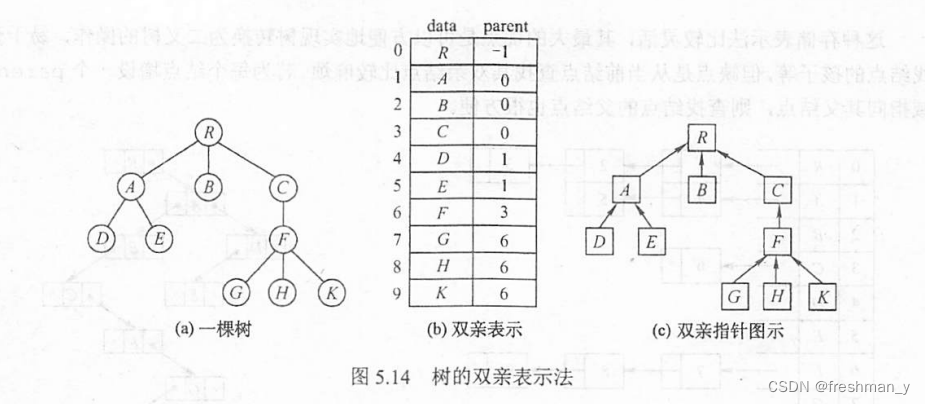
双亲表示法的存储结构描述如下:
#define MAX_TREE_SIZE 100 //树中最多结点数
typedef struct{ //树的结点定义
ElemType data; //数据元素
int parent; //双亲位置域
}PTNode;
typedef struct{ //树的类型定义
PTNode nodes[MAX_TREE_SIZE]; //双亲表示
int n; //结点数
}PTree;2.孩子表示法

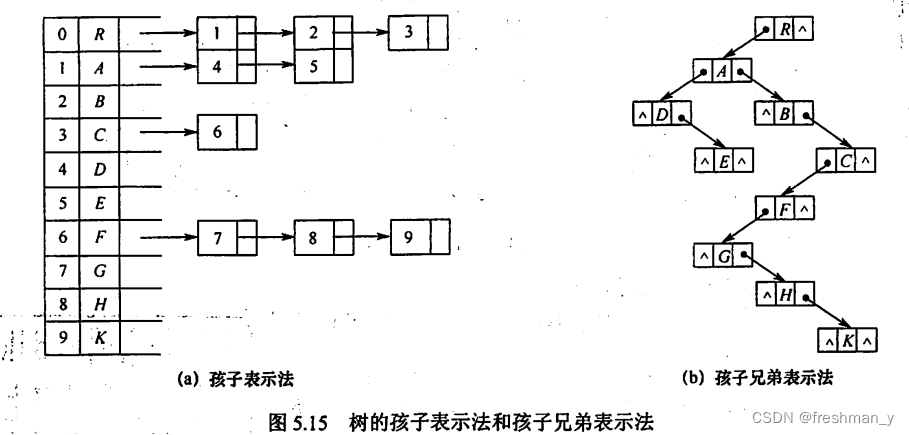
3.孩子兄弟表示法
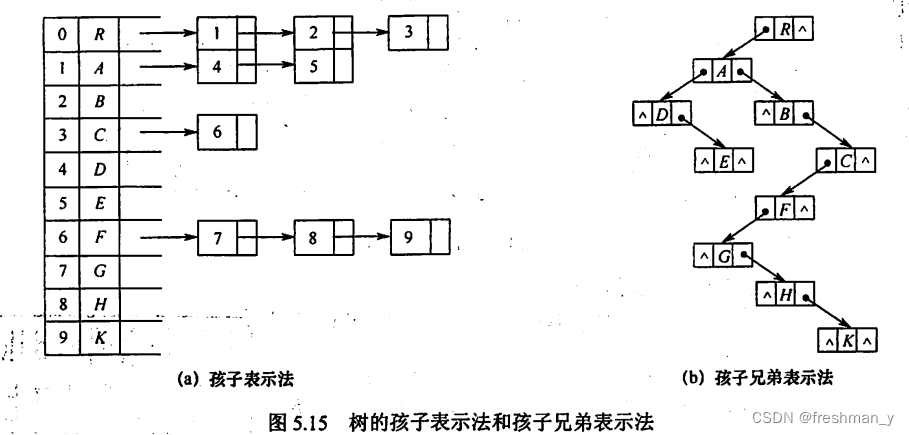
孩子兄弟表示法的存储结构描述如下:
typedef struct CSNode{
ElemType data; //数据域
struct CSNode *firstchild,*nextsibling; //第一个孩子和右兄弟指针
}CSNode,*CSTree;5.5.1哈夫曼树和哈夫曼编码
2.哈夫曼树的构造
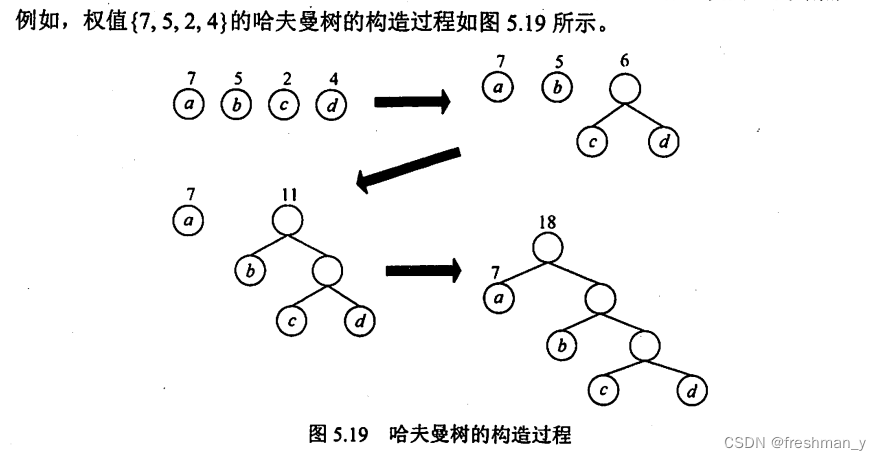
5.5.2并查集
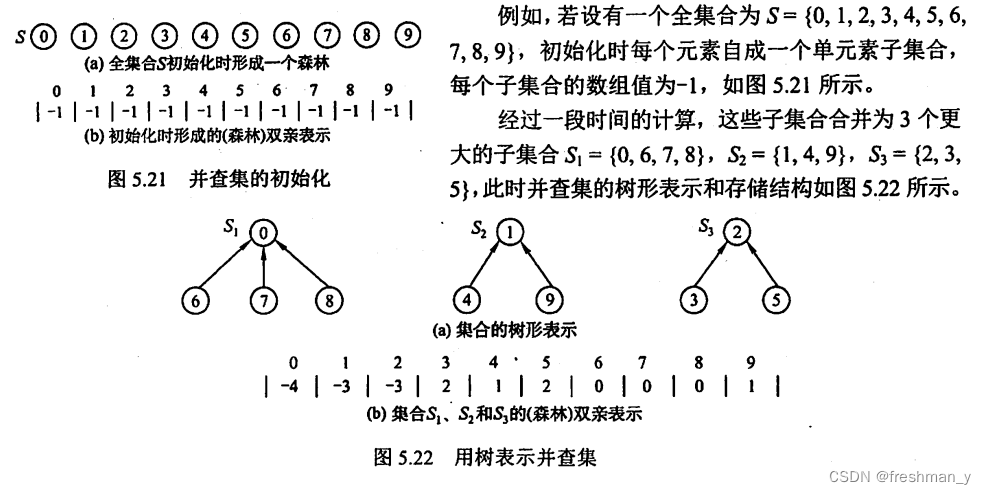

1)并查集的结构定义如下:
#define SIZE 100
int UFSets[SIZE]; //集合元素数组(双亲指针数组)2)并查集的初始化操作(S即为并查集):
void Initial(int S[]){
for(int i=0;i<SIZE;i++) //每个自成单元元素集合
S[i]=1;
}3)Find操作(函数在并查集S中查找并返回包含元素x的树的根):
int Find(int S[],int x){
while(S[x]>=0) //循环寻找x的根
x=S[i];
return x; //根的S[]小于0
}4)Union操作(函数求两个不相交子集合的并集):
void Union(int S[],int Root1,int Root2){
if(Root1==Root2) return; //要求Root1和Root2是不同的集合
S[Root2]=Root1; //将根Root2连接到另一根Root1下面
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号