外接球内切球问题

正方体长方体问题

外接球

\[2R=\sqrt{a^2+b^2+c^2}\notag \]

正方体时,令a=b=c

\[2R=\sqrt3a\notag \]

内切球

\[2R=a\notag \]

棱切球

\[2R=\sqrt2a\notag \]

半球

法一

补为(a,a,2a)的长方体

\[2R=\sqrt{a^2+a^2+4a^2}\notag \]

法二

找出圆心

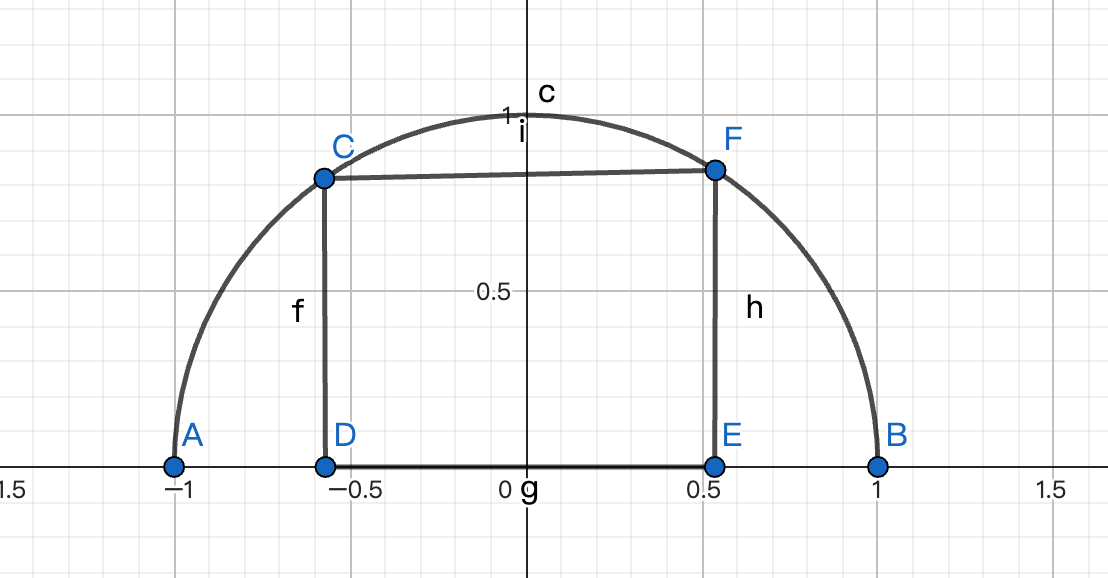
\[CD=1\\ CF=\sqrt2\notag \]

结论

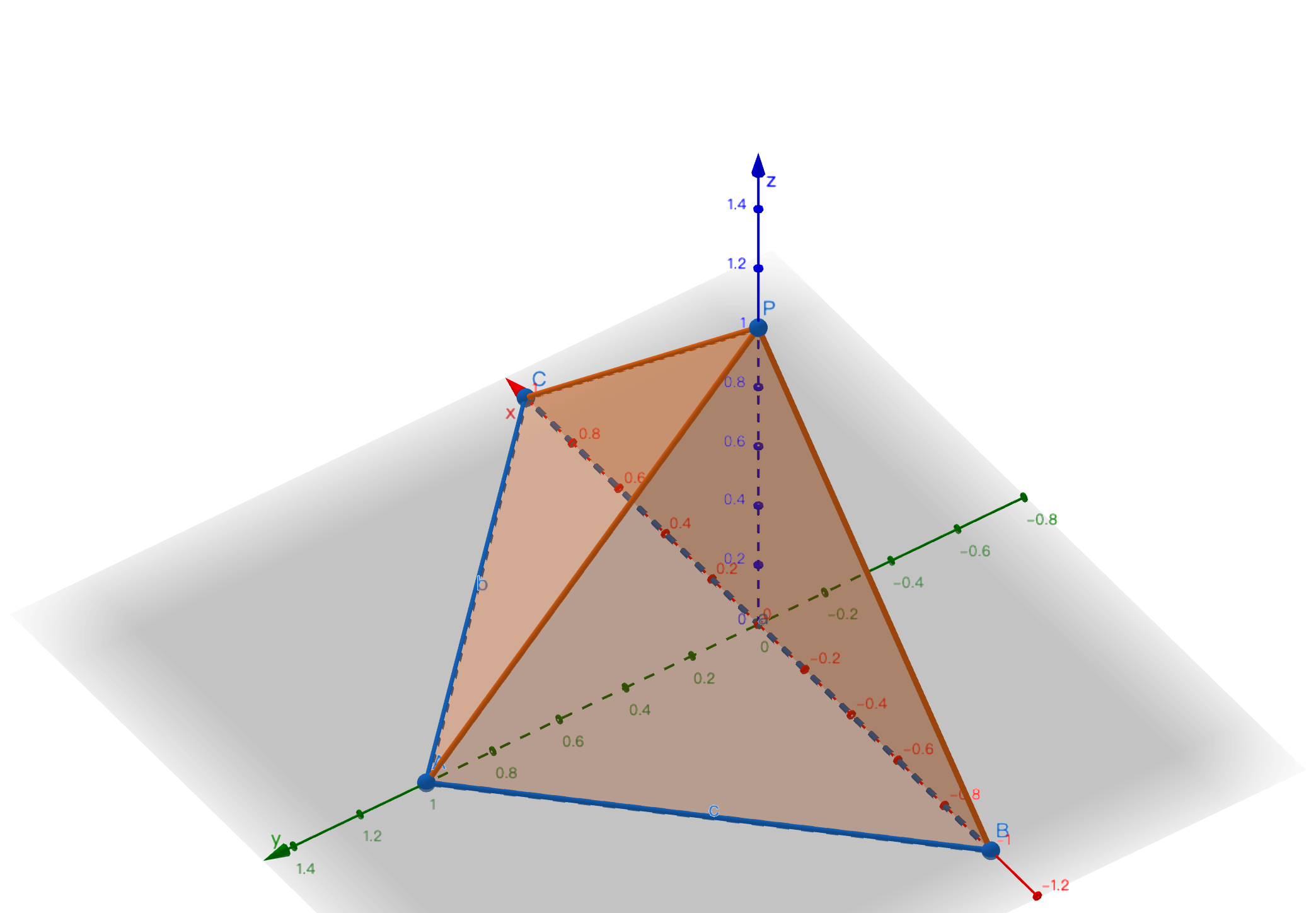
在\(P-ABC\)中

若\(PA=PB=PC\),则\(P'\)为\(ABC\)外心

若P到底面各边距离相等,则\(P'\)为\(ABC\)内心

若\(PA,PB,PC\)两两垂直,则\(P'\)为垂心