数据结构3——浅谈zkw线段树
MENU
1、建树(普通)
2、普通操作*4
3、差分思想*5
本文作者frankchenfu,blogs网址http://www.cnblogs.com/frankchenfu/,转载请保留此文字。
重新修改于2020.9.2
线段树是所有数据结构中,最常用的之一。线段树的功能多样,既可以代替树状数组完成“区间和”查询,也可以完成一些所谓“动态RMQ”(可修改的区间最值问题)的操作。其中,它们大部分都是由递归实现的,因此就有一些问题——栈空间占用大和常数大。
因此,从中便衍生了一种非递归式的线段树(作者是THU的张昆玮,参见他自己的PPT讲稿《统计的力量-线段树》),命名为zkw线段树。
以下内容均用zkw线段树保存区间最大值作为演示。如果代码细节上有问题,请大家以自己写的为准,也欢迎向我反馈。
1、建树
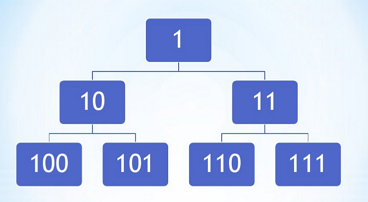
我们可以先观察左边面这张图。用二进制表示出了各个节点的编号。从中,我们可以发现最底层的节点舍去最低位,也就是说向右移一位之后,就变成了他们的父节点。同理,第二层中的结点也可以通过相同的方式变成根节点。
因此,我们在构建这棵树时,这些二进制上的性质,达到代码实现简单,并且效率高的目的。
zkw线段树的操作几乎没有出现递归,而是用循环代替。例如建树操作(d数组存储数值):
void build(int n) { for(bit=1;bit<=n+1;bit<<=1); for(int i=bit+1;i<=bit+n;i++) scanf("%d",&d[i]); for(int i=bit-1;i;i--) d[i]=max(d[i<<1],d[i<<1|1]); //i<<1|1 = (i<<1)+1 = 2*i+1 }
(这里解释一下,bit表示非叶子节点,即倒二层及以上的节点数,每个节点保存的是它的值,如:和,最大值,最小值……)
建树的思想就是,首先完成叶子结点的内容,然后一步一步往上推父亲结点的值。这和普通线段树一样,只不过他用循环直接从底层开始。
而普通的线段树建树则类似于(代码来自这里):
struct SegTreeNode { int val; }segTree[MAXNUM];//定义线段树 void build(int root, int arr[], int istart, int iend) { if(istart == iend)//叶子节点 segTree[root].val = arr[istart]; else { int mid = (istart + iend) / 2; build(root*2+1, arr, istart, mid);//递归构造左子树 build(root*2+2, arr, mid+1, iend);//递归构造右子树 //根据左右子树根节点的值,更新当前根节点的值 segTree[root].val = min(segTree[root*2+1].val, segTree[root*2+2].val); } }
很简单的例子,说明了zkw线段树不仅不需要递归,而且在代码上也更简洁。
2、普通操作
既然是线段树,那么就肯定能完成修改与查询操作。
2.1 单点修改——二进制思想的运用
单点修改也不难,他的思想就是先把叶节点修改,然后依次维护父节点(把所有和它有关的的修改掉)。例如这样:
void update(int x,int y) { for(d[x+=bit]=y,x>>=1;x;x>>=1) d[x]=max(d[x<<1],d[x<<1|1]); }
这个代码就更为简短了(这里就不拿出来对比了)。他的思想就是,修改了叶子结点,只会对他往上到根一条直直的链上的值产生影响——那么自然修改完叶节点往上推就好了。
当然,如果不是整个修改,而是加上或减去某数,只需要将for循环中的 d[x+=bit]=y 改为 d[x+=bit]+=y 即可(这里统一用整体修改作示范,下同)。
2.2 单点查询——最简单的查询
假设数组中有 x 个元素,二叉树层数为 m,那么这 x 个元素在这个满二叉树中的编号就是$2^m$和$2^m+x-1$之间,即第x个元素就是$2^m+x-1$,访问起来很方便。
2.3 区间查询——单点查询的升级版
区间查询也不难,规律同上,就是从两个端点沿区间往上找。不过往上找的时候,你们要注意每个点是否能取得到。比如说你在查询 [1,8] 区间的最大值的时候会遇到两种情况:线段树从 [3,4] 区间往上跳一层是 [1,4] 区间,但是[1,4]区间的最大值很可能不在 [3,4] 内,不能采用;而也有可能是 [7,8] 区间,上面是 [5,8] 区间显然也在,那自然就需要采用(因为你不会再访问里面的 [5,6] 区间了,zkw线段树只会访问两侧端点周围的区间)。怎么判断采不采用呢?我们就发现,如果左端点编号是的结点,那么他包括的区间(或者说两个子区间)都会在左端点的右边,也就是必然可以取到;右端点是奇数的区间,两个子区间必然都在右端点的左侧。这个规律很显然,不理解画个图就好了,不做详细证明。
这里就直接上代码。
int query(int s,int t) { int ans=-1; for(s+=bit-1,t+=bit+1;s^t^1;s>>=1,t>>=1) { if(~s&1) ans=max(ans,d[s^1]); if(t&1) ans=max(ans,d[t^1]); } return ans; }
2.4 区间修改——差分思想
区间修改这时候看起来就很难办了……呃,怎么办呢??
经过思考,笔者发现,用上述代码的思想似乎较难完成O($log_2$ n)级别的区间修改。这时候,翻开zkw神犇PPT讲稿,发现……原来,可以用差分的思想。(事实上,在普通线段树中,可以使用“懒标记”思想,不过限于作者水平,这里不再展开讨论)
3、差分思想
差分?(似乎这个现在叫标记永久化更多一点?还是不同的东西我也不知道)
差分是化绝对为相对的重要手段。我们接下来,数组里的d值就不在存最大值$d_n$了,而是另外开个数组m,存$m_n = d_n - d_{\frac{n}{2}} $,让每一个结点的值都是存他与他父亲结点的差值。
有什么用吗?
当然有(不然说了干什么)!这时候,我们进行区间修改,就只需要修改两次$m_n$的值,也就是说我们本来需要每个点都做一遍单点修改,但是现在我们用类似之前区间查询的办法,只从两侧修改 $O(\log n)$ 个点和父亲的差值,差值修改的量就是这次新加上去的值,这样就等效于直接做完了区间修改的内容。
所以区间修改此时就用类似区间查询的方法完成修改,当然这时修改的只是和父亲的差值,所以复杂度和实现上都相当于两个单点修改;查询一样从两侧结点一直改到根结点,然后记得把差分掉的值后缀和回来,就可以找到答案(这个应该很好理解吧)。
小插曲
然后,我们在写代码的时候会发现,如果我们把d数组初始化为0的话,那么所有的修改都记在数组m中,d数组的值会变吗?不会。
因此,我们干脆连值也不存了,把差分的“标记”直接当作值(所以可能叫做标记永久化吧)。于是,基本的差分思想就出来了。
不过,值得一提的是,在常数上,差分的写法可能更大一些(不一定会明显优于递归版的普通线段树)。
3.1 差分思想与建树
这时候,每个点就像前面说的,存差就好了。代码如下,应该很好理解:
void build(int n) { for(bit=1;bit<=n+1;bit<<=1); for(int i=bit+1;i<=bit+n;i++) scanf("%d",&d[i]); for(int i=bit-1;i;i--) { d[i]=min(d[i<<1],d[i<<1|1]); d[i<<1]-=d[i];d[i<<1|1]-=d[i]; } }
3.2 差分思想与单点修改
你当然可以尝试区间修改,然后用像 query(1,1,x) 这样的方法修改。
不过完全没有这个必要。
void update(int s,int t,int x) { int tmp; for(d[s]+=x;s>1;s>>=1) { tmp=max(d[s],d[s^1]);d[s]-=tmp;d[s^1]-=tmp;d[s>>1]+=tmp; s>>=1; } }
3.3差分思想与单点查询
不得不承认,差分思想的运用,唯一一个不好的地方就是单点查询从O(1)变为了O($log_2$ n),但是他可以帮助我们完成区间修改的操作,因此也只好忍受一下了。
因为差分存储方式的运用,相应的,这时候的代码就成了这样:
void query(int x) { int res=0; while(x) res+=d[x],x>>=1; return res; }
3.4差分思想与区间修改
就为了这个区间查询,我们几乎把内容翻了一倍——讲差分存储方式。而这种方式就是能够让我们完成区间修改。修改方式在上面介绍差分作用时提过了,这里就不在赘述了。代码:
void update(int s,int t,int val) { s+=bit;t+=bit;int tmp; if(s==t) { for(d[s]+=val;s>1;s>>=1) { tmp=min(d[s],d[s^1]);d[s]-=tmp;d[s^1]-=tmp;d[s>>1]+=tmp; } return; } for(d[s]+=val,d[t]+=val;s^t^1;s>>=1,t>>=1) { if(~s&1)d[s^1]+ =val; if(t&1) d[t^1]+=val; tmp=min(d[s],d[s^1]);d[s]-=tmp;d[s^1]-=tmp; d[s>>1]+=tmp;tmp=min(d[t],d[t^1]); d[t]-=tmp;d[t^1]-=tmp;d[t>>1]+=tmp; } for(;s>1;s>>=1) { tmp=min(d[s],d[s^1]);d[s]-=tmp;d[s^1]-=tmp;
d[s>>1]+=tmp; } return; }
3.5差分思想与区间查询
区间查询?其实和之前没用差分的差不多,只是把它求出来之后,再把值依层还原回去。
int query(int s,int t) { int lans=0,rans=0,ans; if(s==t) { for(s+=bit;s;s>>=1) lans+=d[s]; return lans; } for(s+=bit,t+=bit;s^t^1;s>>=1,t>>=1) { lans+=d[s];rans+=d[t]; if(~s&1) lans=min(lans,d[s^1]); if(t&1) rans=min(rans,d[t^1]); } lans+=d[s];rans+=d[t]; for(ans=min(lans,rans);s>1;) ans+=d[s>>=1]; return ans; }
值得一提的是差分之后很容易产生各种问题,又不能区间reset或者支持两种以上操作,常数也已经渐渐逼近普通线段树了,所以不建议写。
至此,zkw线段树的基本操作到这里就讲完了。让我们回顾一下,zkw线段树的优点不仅在于常数小,空间小(对于一般情况下的写法),而且好写好调,是一种优秀的数据结构。它的本质是非递归式线段树。希望这篇博客的内容对大家有帮助,满意请在右下方点个赞,谢谢。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号