机器学习课程CIFAR100训练记录
数据集
基本信息
选用的数据集为:CIFAR-100
图片尺寸:\(32\times 32\)
数据集类别数量:100
数据量:60000
数据划分
训练数据跟测试数据按照5:1进行划分。
| 训练数据集 | 测试数据集 | |
|---|---|---|
| 选取总体规模 | 50000 | 10000 |
| 每个标签类的规模 | 500 | 100 |
数据集预处理与加载
利用Pytorch的transforms模块进行数据增强,通过自带的CIFAR-100数据加载器进行数据集加载,具体的数据集预处理与加载封装成Data类,其代码如下。
class Data:
def __init__(self, batch_size, threads):
mean, std = get_statistics()
# 训练集的数据增强
train_transform = transforms.Compose([
# 随机裁剪
torchvision.transforms.RandomCrop(size=(32, 32), padding=4),
# 依概率水平翻转
torchvision.transforms.RandomHorizontalFlip(),
# Tensor化
transforms.ToTensor(),
# 归一化
transforms.Normalize(mean, std),
# 模拟遮掩
Cutout()
])
# 测试集只进行tensor化与归一化
test_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean, std)
])
# 训练集数据类
train_set = torchvision.datasets.CIFAR100(root='./data', train=True, download=True, transform=train_transform)
# 测试集数据类
test_set = torchvision.datasets.CIFAR100(root='./data', train=False, download=True, transform=test_transform)
# 训练集、测试集加载器
self.train = torch.utils.data.DataLoader(train_set, batch_size=batch_size, shuffle=True, num_workers=threads)
self.test = torch.utils.data.DataLoader(test_set, batch_size=batch_size, shuffle=False, num_workers=threads)
self.classes = train_set.classes
在训练数据加载前,将通过transforms模块进行数据增强,其中包括随机裁剪、依概率水平翻转、数据转化为Tensor、按照均值和标准差归一化以及Cutout。而测试集只进行转化为Tensor与归一化。
获取均值与标准差的函数get_statistics代码如下。
def get_statistics():
# 获取数据集的均值与标准差
train_set = torchvision.datasets.CIFAR100(root="./data", train=True, download=True,
transform=transforms.ToTensor())
data = torch.cat([data[0] for data in DataLoader(train_set)])
return data.mean(dim=[0, 2, 3]), data.std(dim=[0, 2, 3])
Cutout是一种模拟遮挡的数据增强方法,目的是提高泛化能力。该方法随机选择一个固定大小的正方形区域,然后采用全0填充。Cutout方法包装成了Cutout类,该类的代码如下。
class Cutout:
def __init__(self, size=16, p=0.5):
self.size = size
self.half_size = size // 2
self.p = p
def __call__(self, image):
# 取一个随机的tensor值,如果大于p则返回image
if torch.rand([1]).item() > self.p:
return image
# 否则图片部分需要取0,设置的左侧、顶部为[-half, image_size - half]范围的均匀分布采样
left = torch.randint(-self.half_size, image.size(1) - self.half_size, [1]).item()
top = torch.randint(-self.half_size, image.size(2) - self.half_size, [1]).item()
# 右侧和底部与原来的尺寸比较取小
right = min(image.size(1), left + self.size)
bottom = min(image.size(2), top + self.size)
# 对所有图片的对应部分设置为0
image[:, max(0, left): right, max(0, top): bottom] = 0
return image
模型选择
WRN模型介绍
WRN(Wide ResNet)是ResNet的一种变体,通过将卷积层进行宽度拓展达到训练速度更快、同等参数量的ResNet对比下相同甚至更好的效果。本次作业选取的是WRN 34*10,34代表了卷积层个数,10代表了宽度因子(即卷积层的宽度)。其中的各组块结构如下表所示。
| 组名 | 输出大小 | 区块结构 |
|---|---|---|
| 0_convolution | \(32\times 32\) | \([3\times 3,16]\) |
| 1_block | \(32\times 32\) | \(\begin{bmatrix}3\times 3, 16\times 10\\3\times3,16\times 10\end{bmatrix}\times 5\) |
| 2_block | \(16\times 16\) | \(\begin{bmatrix}3\times 3, 32\times 10\\3\times3,32\times 10\end{bmatrix}\times 5\) |
| 3_block | \(8\times 8\) | \(\begin{bmatrix}3\times 3, 64\times 10\\3\times3,64\times 10\end{bmatrix}\times 5\) |
| 6_pooling | \(1\times 1\) | \([8\times 8]\) |
WRN的具体模型代码如下,34*10情况下的宽度因子为10,区块深度为5。区块深度的计算为:\(N = \frac{(depth - 4)}{6}\)。注意:这里下采样单元包含了1_block、2_block、3_block的首个block,因此\(N\)还需要减1。
class WideResNet(nn.Module):
def __init__(self, depth: int, width_factor: int, dropout: float, in_channels: int, labels: int):
super(WideResNet, self).__init__()
#
self.filters = [16, 1 * 16 * width_factor, 2 * 16 * width_factor, 4 * 16 * width_factor]
self.block_depth = (depth - 4) // (3 * 2) - 1
self.f = nn.Sequential(OrderedDict([
("0_convolution", nn.Conv2d(in_channels, self.filters[0], (3, 3), stride=1, padding=1, bias=False)),
("1_block", Block(self.filters[0], self.filters[1], 1, self.block_depth, dropout)),
("2_block", Block(self.filters[1], self.filters[2], 2, self.block_depth, dropout)),
("3_block", Block(self.filters[2], self.filters[3], 2, self.block_depth, dropout)),
("4_normalization", nn.BatchNorm2d(self.filters[3])),
("5_activation", nn.ReLU(inplace=True)),
("6_pooling", nn.AvgPool2d(kernel_size=8)),
("7_flattening", nn.Flatten()),
("8_classification", nn.Linear(in_features=self.filters[3], out_features=labels)),
]))
self._initialize()
def _initialize(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight.data, mode="fan_in", nonlinearity="relu")
if m.bias is not None:
m.bias.data.zero_()
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
elif isinstance(m, nn.Linear):
m.weight.data.zero_()
m.bias.data.zero_()
def forward(self, x):
return self.f(x)
不同单元结构
其中的Block结构代码如下,其包含一个下采样单元与一个深度为4的基础单元。
class Block(nn.Module):
def __init__(self, in_channels: int, out_channels: int, stride: int, depth: int, dropout: float):
super(Block, self).__init__()
self.block = nn.Sequential(
DownsampleUnit(in_channels, out_channels, stride, dropout),
*(BasicUnit(out_channels, dropout) for _ in range(depth))
)
def forward(self, x):
return self.block(x)
其中下采样单元的代码如下,该单元代表1_block、2_block、3_block各组中的首个block以及一个下采样卷积,需要改变tensor的维度,所以首个block的残差项(residual)要用一个1*1的卷积下采样匹配输入输出的不同维度。
class DownsampleUnit(nn.Module):
def __init__(self, in_channels: int, out_channels: int, stride: int, dropout: float):
super(DownsampleUnit, self).__init__()
self.norm_act = nn.Sequential(OrderedDict([
("0_normalization", nn.BatchNorm2d(in_channels)),
("1_activation", nn.ReLU(inplace=True)),
]))
self.block = nn.Sequential(OrderedDict([
("0_convolution", nn.Conv2d(in_channels, out_channels, (3, 3), stride=stride, padding=1, bias=False)),
("1_normalization", nn.BatchNorm2d(out_channels)),
("2_activation", nn.ReLU(inplace=True)),
("3_dropout", nn.Dropout(dropout, inplace=True)),
("4_convolution", nn.Conv2d(out_channels, out_channels, (3, 3), stride=1, padding=1, bias=False)),
]))
self.downsample = nn.Conv2d(in_channels, out_channels, (1, 1), stride=stride, padding=0, bias=False)
def forward(self, x):
x = self.norm_act(x)
return self.block(x) + self.downsample(x)
其中基础单元的代码如下,每个block包含了两个主干卷积。
class BasicUnit(nn.Module):
def __init__(self, channels: int, dropout: float):
super(BasicUnit, self).__init__()
self.block = nn.Sequential(OrderedDict([
# 特定channel数的BN2d层
("0_normalization", nn.BatchNorm2d(channels)),
# 激活函数ReLU
("1_activation", nn.ReLU(inplace=True)),
# channel宽度的3*3卷积层
("2_convolution", nn.Conv2d(channels, channels, (3, 3), stride=1, padding=1, bias=False)),
("3_normalization", nn.BatchNorm2d(channels)),
("4_activation", nn.ReLU(inplace=True)),
("5_dropout", nn.Dropout(dropout, inplace=True)),
("6_convolution", nn.Conv2d(channels, channels, (3, 3), stride=1, padding=1, bias=False)),
]))
def forward(self, x):
return x + self.block(x)
优化策略
学习率衰减
在模型训练过程中,我们采用的学习率衰减是根据回合数变化进行降低调节以提高训练效果。在总回合数的\([0, \frac{2}{10})\)时学习率保持不变,当进行到总回合数的\([\frac{1}{5},\frac{5}{10}),[\frac{5}{10},\frac{7}{10})、[\frac{7}{10},\frac{7.5}{10})、[\frac{7.5}{10},\frac{8.5}{10})、[\frac{8.5}{10},1]\)进度时乘以\(0.2\)。当进行200个回合训练时,该学习率变化如图所示。
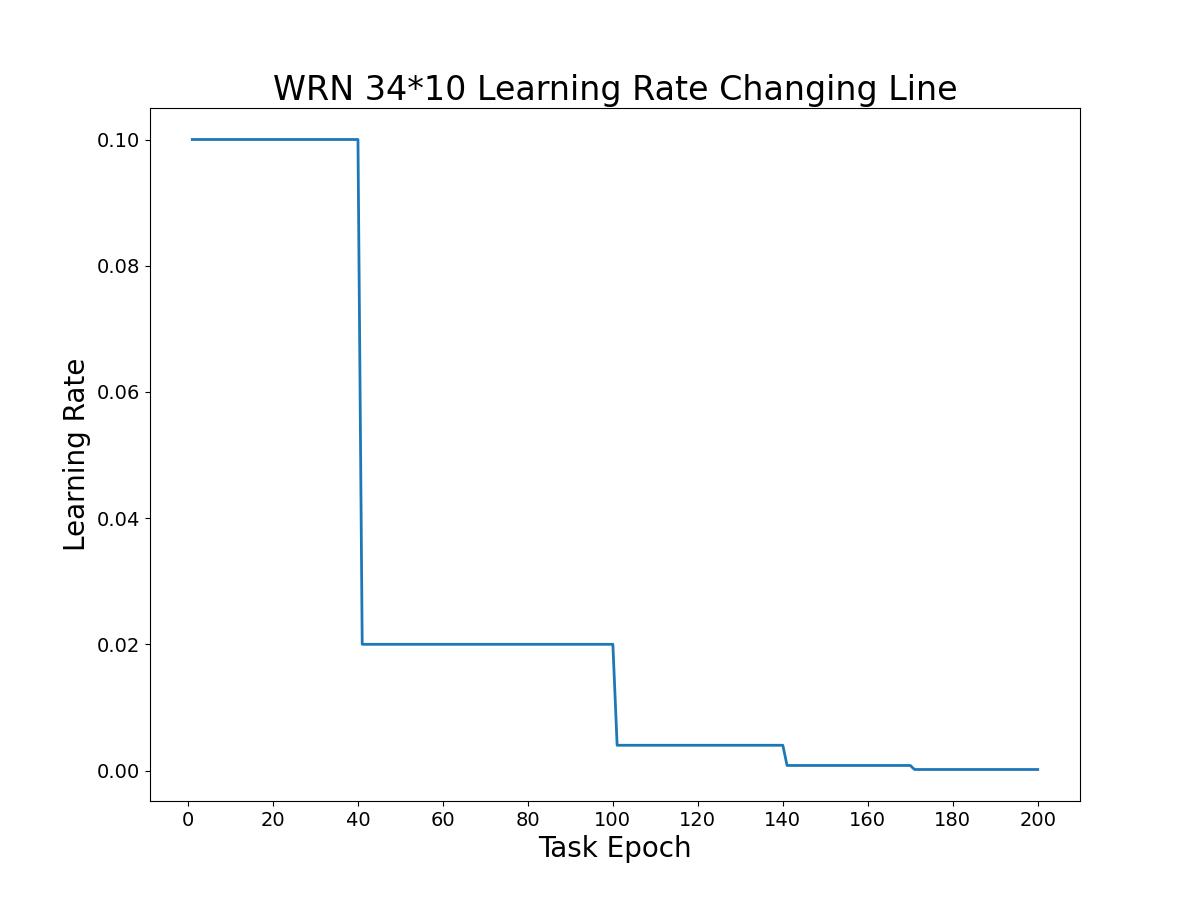
具体的学习率衰减代码如下。
class StepLR:
def __init__(self, optimizer, learning_rate: float, total_epochs: int):
self.optimizer = optimizer
self.total_epochs = total_epochs
self.base = learning_rate
def __call__(self, epoch):
if epoch < self.total_epochs * 2 / 10:
lr = self.base
elif epoch < self.total_epochs * 5 / 10:
lr = self.base * 0.2
elif epoch < self.total_epochs * 7 / 10:
lr = self.base * 0.2 ** 2
elif epoch < self.total_epochs * 8.5 / 10:
lr = self.base * 0.2 ** 3
else:
lr = self.base * 0.2 ** 4
for param_group in self.optimizer.param_groups:
param_group["lr"] = lr
def lr(self) -> float:
return self.optimizer.param_groups[0]["lr"]
SAM优化
SAM(Sharpness Aware Minimization)优化是发表在ICLR'2021上的优化方法,寻找位于具有一致低损失值的邻域中的参数以降低数据集\(S\triangleq \cup^{n}_{i=1}\{(x_i, y_i\}\)在分布\(D\)上的泛化误差。
该优化方法的推导简略如下:
- 根据PAC推导而来的锐度泛化边界(详细推导在论文附录A部分):\(\forall \rho>0\),以高概率在来自\(D\)分布的数据集\(S\)上满足\(L_D(w)\geq \max_\limits{||\epsilon||_2\leq\rho} L_s(w+\epsilon)+h(\frac{||w||^2_2}{\rho^2})\),其中\(h(\cdot):\mathbb{R}_+\rightarrow \mathbb{R}_+\)为严格单调递增函数。
- 将右侧进行重写,得到:\([\max_\limits{||\epsilon||_2\leq\rho}L_S(w+\epsilon)-L_S(w)]+L_S(w)+h(\frac{||w||^2_2}{\rho^2})\)
- 引入正则项\(\lambda||w||^2_2\)近似替代\(h(\frac{||w||^2_2}{\rho^2})\),得到SAM的优化目标:\(\begin{cases}\min_\limits{w}L^{SAM}_S(w)+\lambda||w||^2_2\\L^{SAM}_S(w)\triangleq\max_\limits{||\epsilon||_p\leq\rho}L_S(w+\epsilon)\end{cases}\),\(\rho \geq 0\)且\(\rho \in (1,+\infin)\),这是一个最小最大问题。
- 通过内部最大化的求导以得到一个有效、高效的近似替代\(\nabla_wL^{SAM}_{S}\),泰勒展开\(L_S(w+\epsilon)\),得到:\(\epsilon^*(w)\triangleq \arg\max_\limits{||\epsilon||_p\leq\rho}L_S(w+\epsilon)\approx\arg\max_\limits{||\epsilon||_p\leq\rho} L_S(w)+\epsilon^T\nabla_wL_S(w)\)
- 其中的\(\epsilon\)值通过解决一个经典对偶问题得到:\(\hat{\epsilon}=\frac{\rho \cdot \text{sign}(\nabla_w L_S(w))|\nabla_wL_S(w)|^{q-1}}{(||\nabla_wL_S(w)||^q_q)^{1/p}}\)
- 近似\(\nabla_wL^{SAM}_{S}\),有:\(\nabla_wL^{SAM}_{S}\approx \nabla_wL_S(w+\hat{\epsilon}(w))=\nabla_wL_S(w)|_{w+\hat{\epsilon}(w)}+\frac{d\hat{\epsilon(w)}}{dw}\nabla_wL_S(w)|_{w+\hat{\epsilon}(w)}\)
- 为了加速计算,舍弃第二项得到最终的梯度近似:\(\nabla_wL^{SAM}_{S}(w)\approx\nabla_wL_S(w)|_{w+\hat{\epsilon}(w)}\)
该优化方法的具体步骤如下:
- 采样batch大小的训练集样本
- 根据基础优化算法(SGD、Adam等)计算该batch下的训练损失:\(\nabla_wL_S(w)\)
- 计算\(\hat{\epsilon}=\frac{\rho \cdot \text{sign}(\nabla_w L_S(w))|\nabla_wL_S(w)|^{q-1}}{(||\nabla_wL_S(w)||^q_q)^{1/p}}\),其中:\(\frac{1}{p}+\frac{1}{q}=1\)
- 计算SAM目标的梯度近似值:\(g=\nabla_wL_S^{SAM}\approx \nabla_wL_S(w)|_{w+\hat{\epsilon}(w)}\)
- 更新参数:\(w_{t+1}=w_{t}-\eta g\),其中\(\eta\)为学习率。
- 重复以上步骤直至收敛,得到最终的\(w\)。
SAM优化的具体代码如下。
class SAM(torch.optim.Optimizer):
def __init__(self, params, base_optimizer, rho=0.05, adaptive=False, **kwargs):
assert rho >= 0.0, f"Invalid rho, should be non-negative: {rho}"
defaults = dict(rho=rho, adaptive=adaptive, **kwargs)
super(SAM, self).__init__(params, defaults)
self.base_optimizer = base_optimizer(self.param_groups, **kwargs)
self.param_groups = self.base_optimizer.param_groups
@torch.no_grad()
def first_step(self, zero_grad=False):
grad_norm = self._grad_norm()
for group in self.param_groups:
scale = group["rho"] / (grad_norm + 1e-12)
for p in group["params"]:
if p.grad is None: continue
self.state[p]["old_p"] = p.data.clone()
e_w = (torch.pow(p, 2) if group["adaptive"] else 1.0) * p.grad * scale.to(p)
p.add_(e_w) # climb to the local maximum "w + e(w)"
if zero_grad: self.zero_grad()
@torch.no_grad()
def second_step(self, zero_grad=False):
for group in self.param_groups:
for p in group["params"]:
if p.grad is None: continue
p.data = self.state[p]["old_p"] # get back to "w" from "w + e(w)"
self.base_optimizer.step() # do the actual "sharpness-aware" update
if zero_grad: self.zero_grad()
@torch.no_grad()
def step(self, closure=None):
assert closure is not None, "Sharpness Aware Minimization " \
"requires closure, but it was not provided"
# the closure should do a full forward-backward pass
closure = torch.enable_grad()(closure)
self.first_step(zero_grad=True)
closure()
self.second_step()
def _grad_norm(self):
# put everything on the same device, in case of model parallelism
shared_device = self.param_groups[0]["params"][0].device
norm = torch.norm(
torch.stack([
((torch.abs(p) if group["adaptive"] else 1.0) *
p.grad).norm(p=2).to(shared_device)
for group in self.param_groups for p in group["params"]
if p.grad is not None
]),
p=2
)
return norm
def load_state_dict(self, state_dict):
super().load_state_dict(state_dict)
self.base_optimizer.param_groups = self.param_groups
训练与测试
环境与参数
训练、测试使用的GPU为单块2080Ti,CPU为Intel i9-9900K,内存为32G。
训练与测试的python版本为3.7.6,依赖的python库如下:
pytorch>=1.10.1
pandas>=1.3.5
torchsummary>=1.5.1
torchvision>=0.11.2
matplotlib>=3.5.0
numpy>=1.21.2
训练、测试中的相关参数如下,batch大小为128,WRN的卷积层数为34,训练、测试总回合数为200个回合,SAM的\(\rho\)选取为0.1,WRN的宽度为10,标签平滑的\(\epsilon\)为0.1,初始学习率为0.1。
para_dict = {
"adaptive": False,
"batch_size": 128,
"depth": 34,
"dropout": 0.0,
"epochs": 200,
"label_smoothing": 0.1,
"lr": 0.1,
"momentum": 0.9,
"threads": 8,
"rho": 0.1,
"weight_decay": 0.0005,
"width_factor": 10,
}
具体的参数设定代码如下,SAM优化是在SGD基础上进行的,将SGD得到的梯度锐度进行最小化。
# 结果保留的路径
result_dir = "./result/" + datetime.now().strftime("%Y%m%d-%H%M%S")
# 文件夹创建
mkdir(result_dir)
# 初始化,设定指定的随机数
initial(seed=17)
# 设置显卡设备
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 读取数据集
dataset = Data(para_dict["batch_size"], para_dict["threads"])
# 设置日志
log = Logger(log_each=17)
# WRN 34*10
model = WideResNet(para_dict["depth"], para_dict["width_factor"], para_dict["dropout"], in_channels=3, labels=100).to(device)
# SGD为基础优化器
base_optim = torch.optim.SGD
# SAM为进一步的优化器
optimizer = SAM(model.parameters(), base_optim, rho=para_dict["rho"], adaptive=para_dict["adaptive"],
lr=para_dict["lr"], momentum=para_dict["momentum"], weight_decay=para_dict["weight_decay"])
# 学习率的调节,根据epoch的数量进行调节
scheduler = StepLR(optimizer, para_dict["lr"], para_dict["epochs"])
损失函数
选取的损失函数为交叉熵函数,同时使用了标签平滑。使用标签平滑时的标签分布为:\(q_i=\begin{cases}1-\epsilon, if(i=y)\\ \frac{\epsilon}{K-1},if(i\not=y)\end{cases}\),\(K\)为类别的个数,\(\epsilon\)为超参数。
交叉熵函数:\(Loss_i=-\sum^K_{i=1}q_i\log p_i\)。
带标签平滑的交叉熵函数代码如下。
def sce(pred, gold, smoothing=0.1):
# Smooth Cross Entropy
n_class = pred.size(1)
one_hot = torch.full_like(pred, fill_value=smoothing / (n_class - 1))
one_hot.scatter_(dim=1, index=gold.unsqueeze(1), value=1.0 - smoothing)
log_prob = F.log_softmax(pred, dim=1)
return F.kl_div(input=log_prob, target=one_hot, reduction='none').sum(-1)
训练与测试代码
模型训练、测试的代码如下,将根据之前的参数进行200个epoch的WRN模型训练与测试。
for epoch in range(para_dict["epochs"]):
# 进行模型训练
model.train()
log.train(len_dataset=len(dataset.train))
for batch in dataset.train:
# 读取输入以及标签
inputs, targets = (b.to(device) for b in batch)
# 恢复训练现场,并恢复BN momentum
enable_running_status(model)
# 进行模型当前batch的训练
predictions = model(inputs)
# 计算损失,使用smooth cross entropy
loss = sce(predictions, targets, smoothing=para_dict["label_smoothing"])
# 使用当前梯度损失均值进行反向传播
loss.mean().backward()
# SAM第一次forward-backward步骤
optimizer.first_step(zero_grad=True)
# 记录训练现场,并清空BN momentum
disable_running_status(model)
sce(model(inputs), targets, smoothing=para_dict["label_smoothing"]).mean().backward()
# SAM第二次forward-backward步骤
optimizer.second_step(zero_grad=True)
# 模型进行训练评价,获取当前计算分布中概率最大的结果
with torch.no_grad():
correct = torch.argmax(predictions.data, 1) == targets
# 日志输出
log(model, loss.cpu(), correct.cpu(), scheduler.lr())
# 调节学习率
scheduler(epoch)
# 进行模型测试
model.eval()
log.eval(len_dataset=len(dataset.test))
# 用测试集评价当前测试结果
with torch.no_grad():
topk = 0
for batch in dataset.test:
inputs, targets = (b.to(device) for b in batch)
predictions = model(inputs)
_, maxk = torch.topk(predictions, 5, dim=-1)
loss = sce(predictions, targets, smoothing=para_dict["label_smoothing"])
correct = torch.argmax(predictions, 1) == targets
targets = targets.view(-1, 1)
topk = (targets == maxk)
log(model, loss.cpu(), correct.cpu(), topk=topk)
if epoch % 5 == 0:
torch.save(model, result_dir+"/"+str(epoch)+".pt")
log.flush()
其中,调用的initial函数为设置初始种子的函数,具体代码如下。
def initial(seed: int):
# 设置随机数种子
random.seed(seed)
# 设置torch随机数种子
torch.manual_seed(seed)
# 设置cuda中随机数种子
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
# 启动torch后端的cudnn
torch.backends.cudnn.enabled = True
torch.backends.cudnn.benchmark = True
torch.backends.cudnn.deterministic = False
调用的disable_running_status函数是实现BN层的冻结,避免对模型测试的影响,该函数的代码如下。
def disable_running_status(model):
def _disable(module):
if isinstance(model, nn.BatchNorm2d):
# 保存当前BN的momentum到module.backup_momentum进行现场保存
module.backup_momentum = module.momentum
# 将momentum清空
module.momentum = 0
model.apply(_disable)
调用的enable_running_status函数则是实现BN层的解冻以继续训练,该函数的代码如下。
def enable_running_status(model):
def _enable(module):
if isinstance(module, nn.BatchNorm2d) and hasattr(module, "backup_momentum"):
# 检查BN以及备份的字段并恢复现场
module.momentum = module.backup_momentum
model.apply(_enable)
结果分析
根据损失值、准确率进行结果的分析。
损失值比较
WRN 34*10模型在200个回合中的训练损失曲线与测试损失曲线如下图所示。
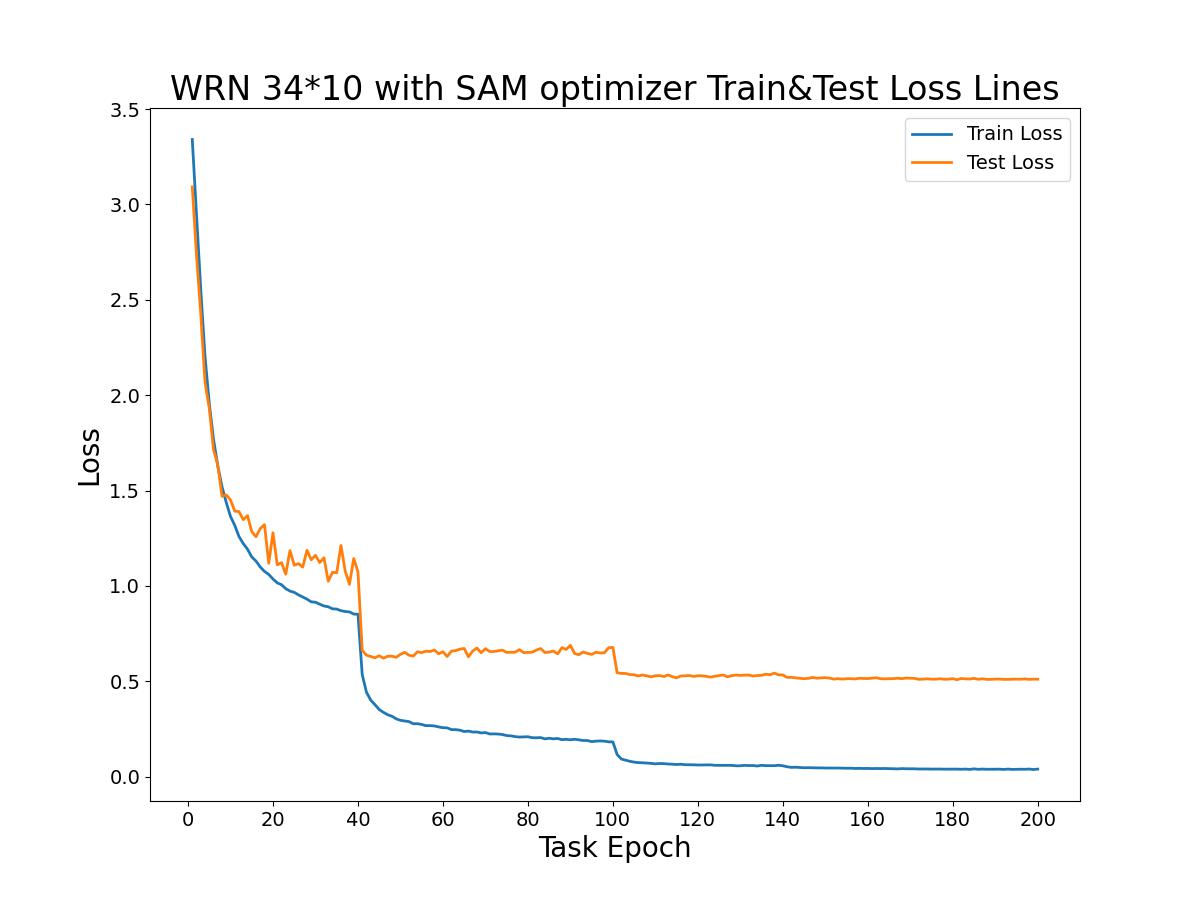
从损失曲线比较中可以看出:在前40个回合中训练损失与测试损失的差距比较小,但损失值都偏大;当第40个回合时学习率变小后,模型的训练损失与测试损失明显再一次降低,但两者差距逐渐变大;在第100个回合学习率进一步变小后损失值也出现了明显的降低,此后两者的损失差距较大,但差距值变化幅度小,同时在第140、170回合时测试损失也出现小幅度降低,但没之前那么明显。在模型训练、测试中测试误差最小值为0.5081。
准确率比较
Top1准确率是指模型输出最大概率的类别是正确标签的比值,Top5准确率是模型输出最高概率的前五个类别中有包含正确类别的数量与样本数的比值。
Top1准确率
WRN 34*10模型在200个回合中的训练Top1准确率曲线与测试Top1准确率曲线如下图所示。
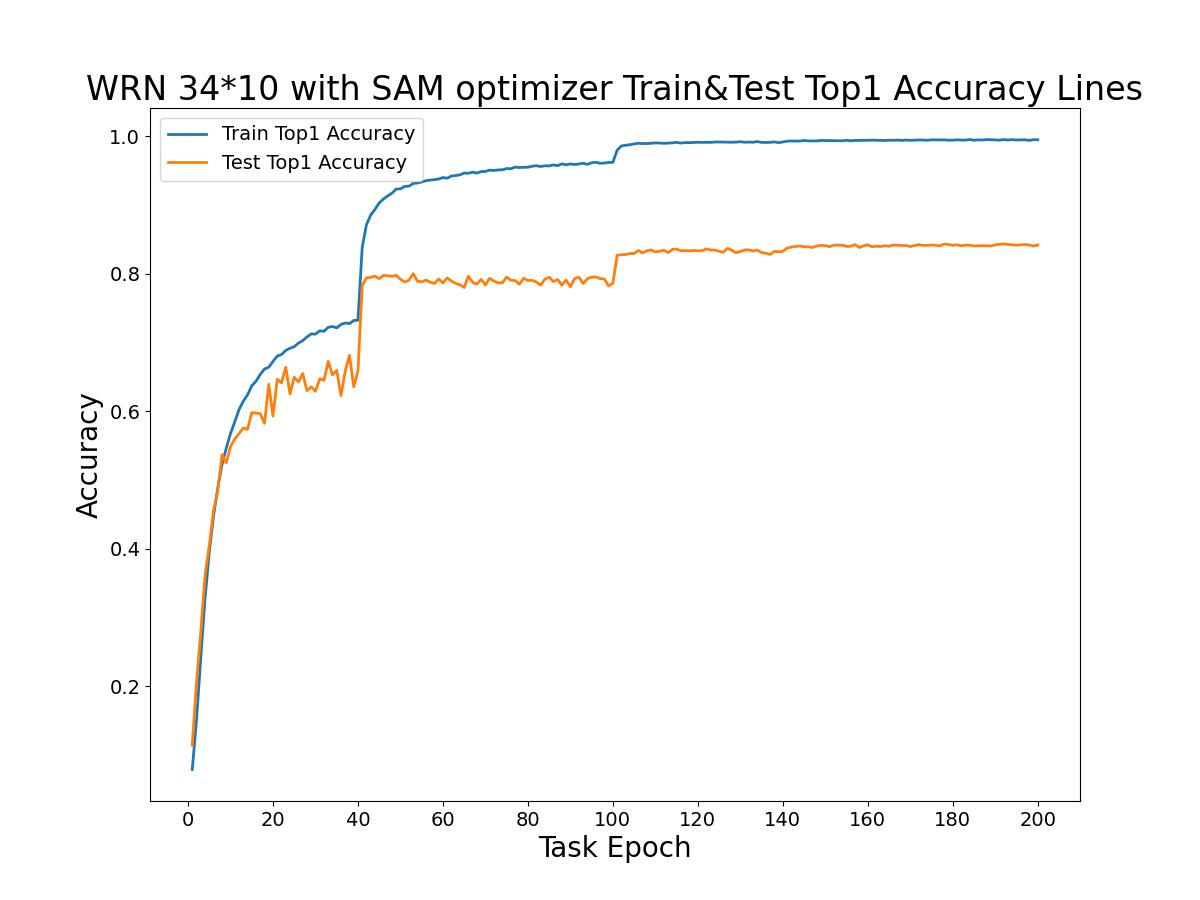
从Top1准确率曲线比较中可以看出:在前40个回合训练准确率与测试准确率差距小,但整体偏低;当经过第40、100回合时学习率降低,准确率都明显提升,但两者差距逐渐变大。当经过第140、170回合时准确率由于学习率的降低而小幅度提升,此时两条曲线的差距变化趋于平稳。测试准确率最高时为0.8436,即84.36%。
Top5准确率
WRN 34*10模型在200个回合中的模型测试Top1准确率曲线与模型测试Top5准确率曲线如下图所示。
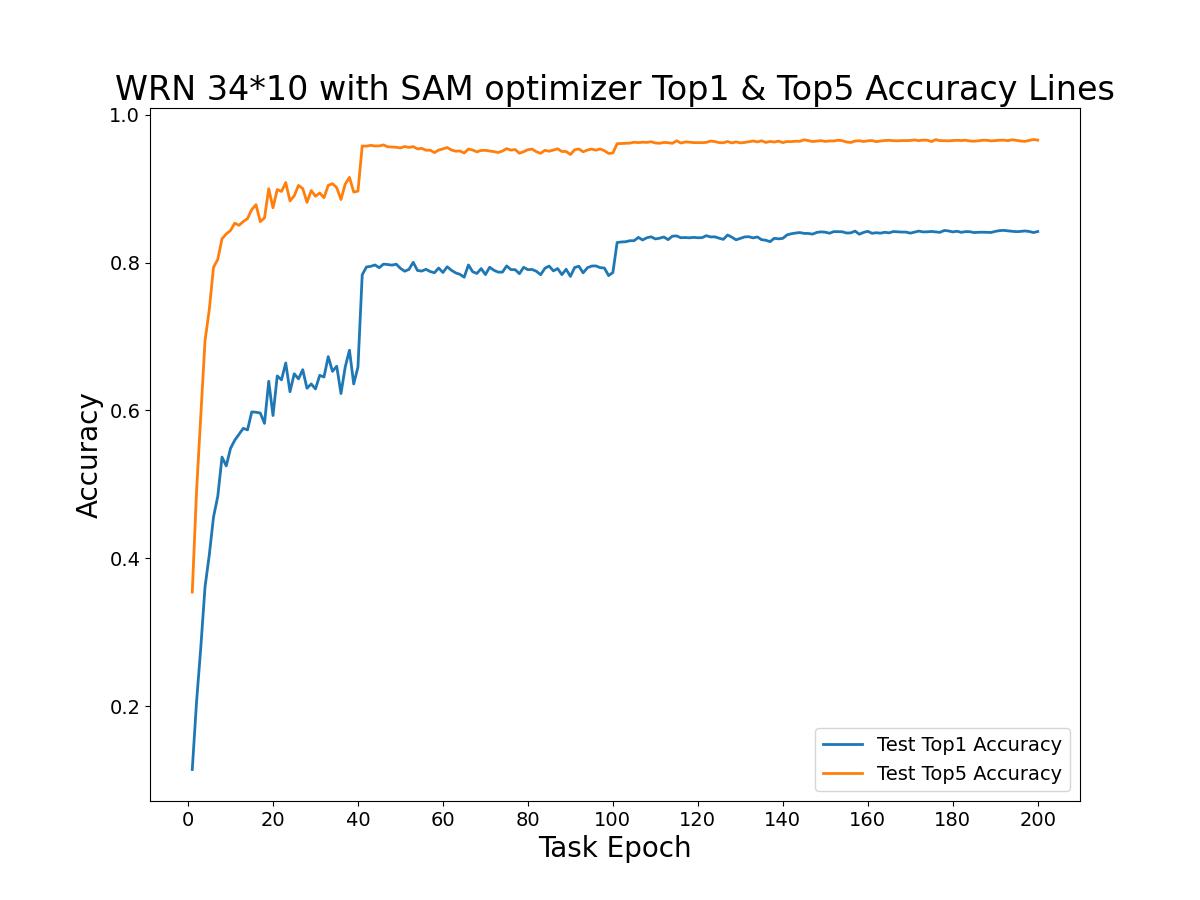
可以看出模型测试时的Top5准确率曲线基本高于模型测试时的Top1准确率曲线,但两者变化的拐点基本一致。模型测试时的Top5准确率最高为0.9665,即96.65%。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号