密码学笔记：块密码

该部分为本科期间密码学课程复习笔记的备份。

Introduction

Block Ciphers are a natural generalization（一般化） of the classical substitution-transposition ciphers.

Block

• divides the plaintext into m blocks of fixed size, and perform the same process on each block to produce m blocks of ciphertext
• The block size can be any number of bits, but is usually large
• All the bits in the cipher block should depend on all the bits in the plaintext block

Process

1. First define a block of computer bits which represent several characters
2. Then Encrypt the complete block at one time

Feistel Structure

In 1973, Feistel suggest a form of product cipher.

product cipher( substitution- permutation (SP) cipher )

1. The overall process involves several stages of a substitution followed by a transposition
2. The master key is subdivided into a set of subkeys – one for each stage
3. At each stage the data block is divided into a left and a right segment, the segments are swapped, and one segment is mixed with subkey for that stage.

数学表述

令F为轮函数，并令\(K_0,K_1,...,K_n\)分别为轮0,1,...,n的子密钥。将明文拆分成两个等长的块\((L_0,R_0)\)。

加密过程

对每轮\(i=0,1,...,n\)，计算：

\[L_{i+1}=R_1 \]

\[R_{i+1}=L_i \bigoplus F(R_i,K_i) \]

则密文为：\((R_{n+1},L_{n+1})\)。

解密过程

对于\((R_{n+1},L_{n+1})\)，通过计算\(i=n,n-1...,0\) :

\[R_i=L_{i+1} \]

\[L_i=R_{i+1}\bigoplus F(L_{i+1},K_i) \]

则明文为\((L_0,R_0)\)。

DES

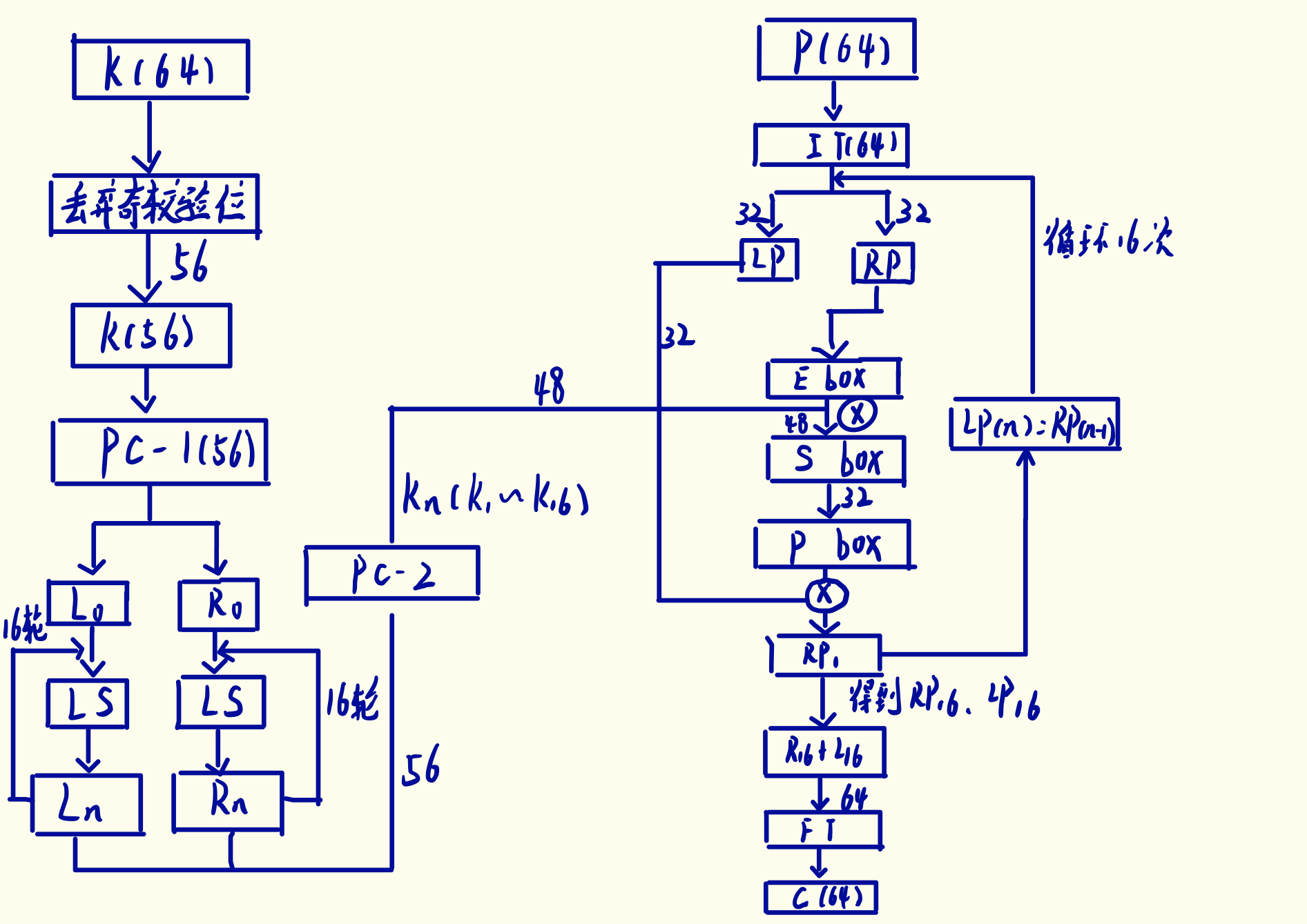
Principle

• substitution-permutation cipher
• 16 SP stages
• DES works on 64 bit blocks
• 56 bit key

Key

The key for DES is an arbitrary 56 bit string of 0 and 1

Often it is given as a 7 letter word

DES expands this key to 64 bits by adding 8 additional 0 and 1

• Bits 8, 16, 24, 32, 40, 48, 56, and 64 are added so that each 8 bit block has odd parity (odd number of ‘0’)（即8, 16, 24, 32, 40, 48, 56,64位为奇偶校验位）
• The key is divided, shifted, and shuffled 16 times to form 16 different (but related) subkeys each of which is 48 bits long

Example

K(64bit) = 133457799BBCDFF1

K(64bit) = 00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001 （加注的bits为奇偶校验位，若前7bits为奇数个1，则校验位为0；如果为偶数个1，则校验位为1）

using 56bit key=0001001 0011010 0101011 0111100 1001101 1011110 1101111 1111000

note：我们提供的一般为64位 key，但实际DES用到的却只有56bits，通过缩小变换表变为56位。

Subkey Generation Process

1. PC-1 置换（64bits变56bits）:Discarding: 8、16、24、32、40、48、56、64 bit
   PC-1（缩小变换表）

   57	49	41	33	25	17	9	1	58	50	42	34	26	18
   10	2	59	51	43	35	27	19	11	3	60	52	44	36
   63	55	47	39	31	23	15	7	62	54	46	38	30	22
   14	6	61	53	45	37	29	21	13	5	28	20	12	4
   (从左向右按行进行数)

2. LSC: one bit in 1、2、9、16 stage, tow bits in other stages（即在第1、2、9、16轮子密钥生成时密钥循环左移1位；在其他轮循环左移2位）

3. PC-2 (Compressing，压缩变换)

   14	17	11	24	1	5	3	28	15	6	21	10
   23	19	12	4	26	8	16	7	27	20	13	2
   41	52	31	37	47	55	30	40	51	45	33	48
   44	49	39	56	34	53	46	42	50	36	29	32

code

def getSubKeys(key):
    res=[]
    key_56=[key[PC_1[i]-1] for i in range(56)]#PC-1变换
    shift_list=[1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]#移位数表
    for i in range(16):#进行16轮子密钥获取
        key_l=shift(key_56[:28],shift_list[i])
        key_r=shift(key_56[28:],shift_list[i])
        key_56=key_l+key_r#分别移位后交换Key_L、Key_R
        key_48=[key_56[PC_2[i]-1] for i in range(48)]#压缩变换
        res.append(key_48)
    return res#返回subkey

Encryption

1. Initial Transposition（初始置换）

   通过初始置换表进行64bits明文的初始置换

   58	50	42	34	26	18	10	2
   60	52	44	36	28	20	12	4
   62	54	46	38	30	22	14	6
   64	56	48	40	32	24	16	8
   57	49	41	33	25	17	9	1
   59	51	43	35	27	19	11	3
   61	53	45	37	29	21	13	5
   63	55	47	39	31	23	15	7

2. Each stage of DES includes some processes, which are defined in three “boxes” called the expansion box (Ebox), the substitution box (Sbox), and the permutation box (Pbox),then XOR

   

• E-Box

  

  EBox-Table
  |||||||||||||
  |-|-|-|-|-|-|-|-|-|-|-|-|-|-|
  |32|1|2|3|4|5|4|5|6|7|8|9|
  |8|9|10|11|12|13|12|13|14|15|16|17|
  |16|17|18|19|20|21|20|21|22|23|24|25|
  |24|25|26|27|28|29|28|29|30|31|32|1|

• S-Box

  

  S1:

  	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  0	14	4	13	1	2	15	11	8	3	10	6	12	5	9	0	7
  1	0	15	7	4	14	2	13	1	10	6	12	11	9	5	3	8
  2	4	1	14	8	13	6	2	11	15	12	9	7	3	10	5	0
  3	15	12	8	2	4	9	1	7	5	11	3	14	10	0	6	13

  S2:

  	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  0	15	1	8	14	6	11	3	4	9	7	2	13	12	0	5	10
  1	3	13	4	7	15	2	8	14	12	0	1	10	6	9	11	5
  2	0	14	7	11	10	4	13	1	5	8	12	6	9	3	2	15
  3	13	8	10	1	3	15	4	2	11	6	7	12	0	5	14	9

  S3

  	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  0	10	0	9	14	6	3	15	5	1	13	12	7	11	4	2	8
  1	13	7	0	9	3	4	6	10	2	8	5	14	12	11	15	1
  2	13	6	4	9	8	15	3	0	11	1	2	12	5	10	14	7
  3	1	10	13	0	6	9	8	7	4	15	14	3	11	5	2	12

  S4:

  	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  0	7	13	14	3	0	6	9	10	1	2	8	5	11	12	4	15
  1	13	8	11	5	6	15	0	3	4	7	2	12	1	10	14	9
  2	10	6	9	0	12	11	7	13	15	1	3	14	5	2	8	4
  3	3	15	0	6	10	1	13	8	9	4	5	11	12	7	2	14

  S5:

  	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  0	2	12	4	1	7	10	11	6	8	5	3	15	13	0	14	9
  1	14	11	2	12	4	7	13	1	5	0	15	10	3	9	8	6
  2	4	2	1	11	10	13	7	8	15	9	12	5	6	3	0	14
  3	11	8	12	7	1	14	2	13	6	15	0	9	10	4	5	3

  S6:

  	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  0	12	1	10	15	9	2	6	8	0	13	3	4	14	7	5	11
  1	10	15	4	2	7	12	9	5	6	1	13	14	0	11	3	8
  2	9	14	15	5	2	8	12	3	7	0	4	10	1	13	11	6
  3	4	3	2	12	9	5	15	10	11	14	1	7	6	0	8	13

  S7:

  	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  0	4	11	2	14	15	0	8	13	3	12	9	7	5	10	6	1
  1	13	0	11	7	4	9	1	10	14	3	5	12	2	15	8	6
  2	1	4	11	13	12	3	7	14	10	15	6	8	0	5	9	2
  3	6	11	13	8	1	4	10	7	9	5	0	15	14	2	3	12

  S8:

  	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  0	13	2	8	4	6	15	11	1	10	9	3	14	5	0	12	7
  1	1	15	13	8	10	3	7	4	12	5	6	11	0	14	9	2
  2	7	11	4	1	9	12	14	2	0	6	10	13	15	3	5	8
  3	2	1	14	7	4	10	8	13	15	12	9	0	3	5	6	11

  note：将6bits分组的第一个bit位与第6个bit位拼在一起，其值为行位置；第2、3、4、5bit位拼在一起，其为作列位置。

• P-Box

  16	7	20	21	29	12	28	17
  1	15	23	26	5	18	31	10
  2	8	24	14	32	27	3	9
  19	13	30	6	22	11	4	25

• XOR

  

3. Final Transposition

   40	8	48	16	56	24	64	32
   39	7	47	15	55	23	63	31
   38	6	46	14	54	22	62	30
   37	5	45	13	53	21	61	29
   36	4	44	12	52	20	60	28
   35	3	43	11	51	19	59	27
   34	2	42	10	50	18	58	26
   33	1	41	9	49	17	57	25

Code

def encrypt(plaintext,key):
    subkeys=getSubKeys(key)#获取子密钥
    text=inputIT(plaintext)#进行初始置换
    for i in range(16):
        text_l=text[:32]
        text_r=text[32:]
        r_extend=extendPlain(text_r)#E-Box变换
        xor1=xor(r_extend,subkeys[i])#与子密钥进行XOR
        res_sBox=SBoxPermutation(xor1)#S-Box变换
        res_pBox=PBoxPermutation(res_sBox)#进行P-Box置换
        res=xor(text_l,res_pBox)#进行PL与进过处理后的PR进行最终XOR
        text=text_r+res#进行换位
    text=text[32:]+text[:32]
    text=inputFT(text)
    return text

SDES

Encryption

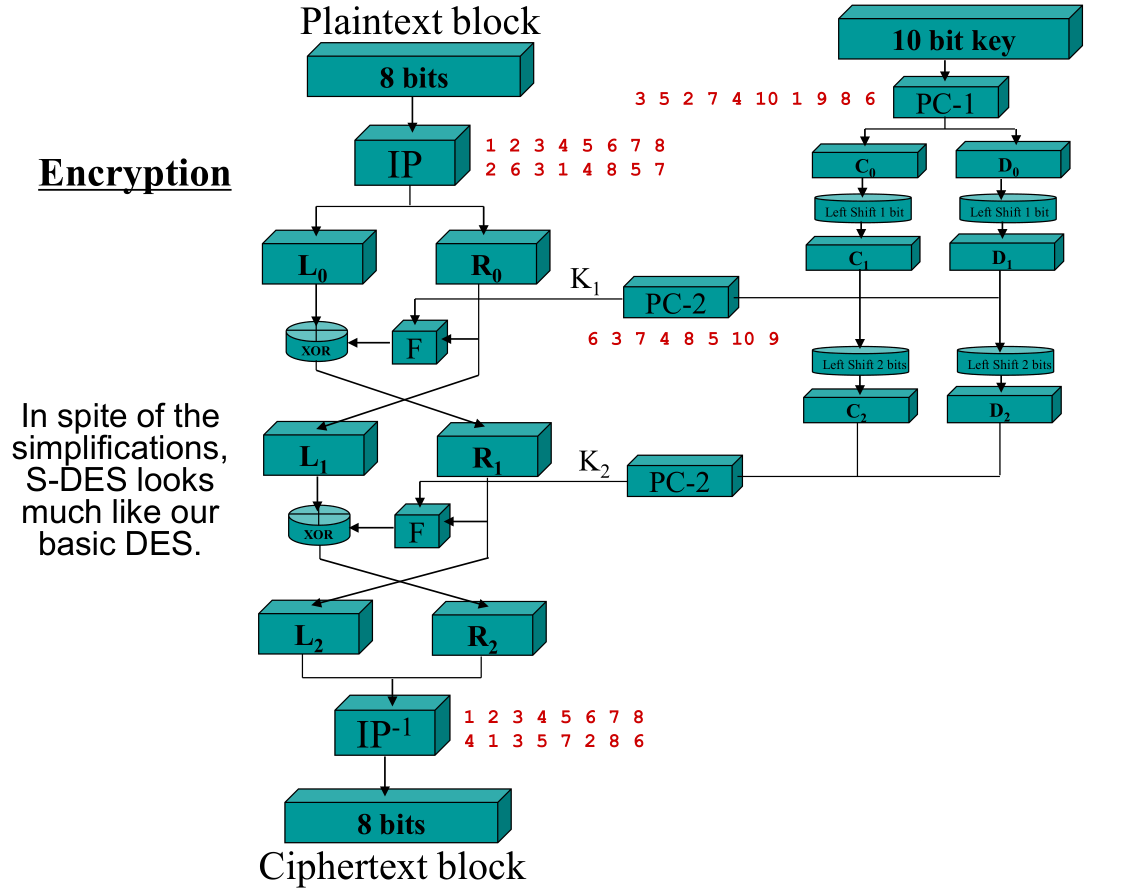
It operates on 8-bit data blocks (in other words, single characters)
using a 10-bit key (only \(2^{10}\) = 1024 possibilities) and two stages

The function F on the prior slide contains an EBox, PBox and 2
SBoxes (much like DES)

• EBox: 4 1 2 3 2 3 4 1
• PBox: 2 4 3 1
• two S-Boxes:

  • The input is a 4 bit value

  • The first and last bits define the row

  • The middle bits define the column

  • The output is a 2 bit value

    \(S_0\):

    	0	1	2	3
    0	1	0	2	3
    1	3	1	0	2
    2	2	0	3	1
    3	1	3	2	0

    \(S_1\):

    	0	1	2	3
    0	0	3	1	2
    1	3	2	0	1
    2	1	0	3	2
    3	2	1	3	0

Decryption

将key转换成subkey之后，subkey进行逆序翻转过来，再经过相同的DES 加密过程

Code

def decrypt(cipher,key):
    subkeys=getSubKeys(key)[::-1]
    text=inputIT(cipher)
    for i in range(16):
        text_l=text[:32]
        text_r=text[32:]
        r_extend=extendPlain(text_r)
        xor1=xor(r_extend,subkeys[i])
        res_sBox=SBoxPermutation(xor1)
        res_pBox=PBoxPermutation(res_sBox)
        res=xor(text_l,res_pBox)
        text=text_r+res
    text=text[32:]+text[:32]
    text=inputFT(text)
    return text

DES FAQ

Why DES has 16 stages?

16 stages is a threshold limit value (TLV)

Does DES key has some weakness?

Yes.

1. The simplest attack to DES is brute-force attack which will test all the feasible keys (\(2^{56}\)).
   • With the development of computer and network, the time reduced greatly.
   • Some analysis algorithms such as differential
2. cryptanalysis and linear cryptanalysis were also suggested to reduce the work
3. Key Weakness
   • One of the early discoveries was that DES had some weak keys:

     • keys that generate the same subkey for each round

     • four such DES keys:

       0101 0101 0101 0101

       FEFE FEFE FEFE FEFE

       1F1F 1F1F 0E0E 0E0E

       E0E0 E0E0 F1F1 F1F1

   • There are also 12 semi-weak DES keys
   • Semi-weak keys generate only two subkeys which alternate rounds

Double DES

Encryption

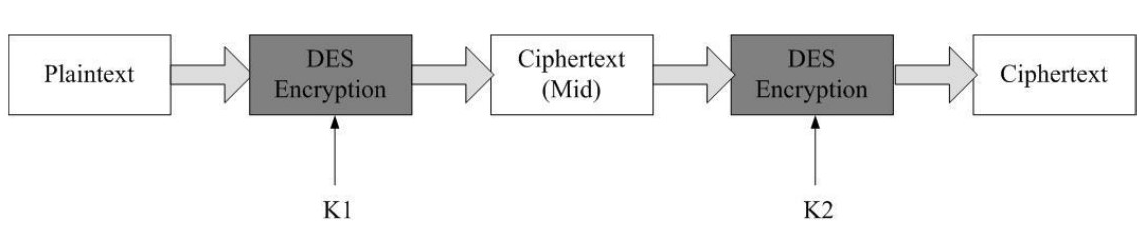
Decryption

Meet-in-the-middle Attack

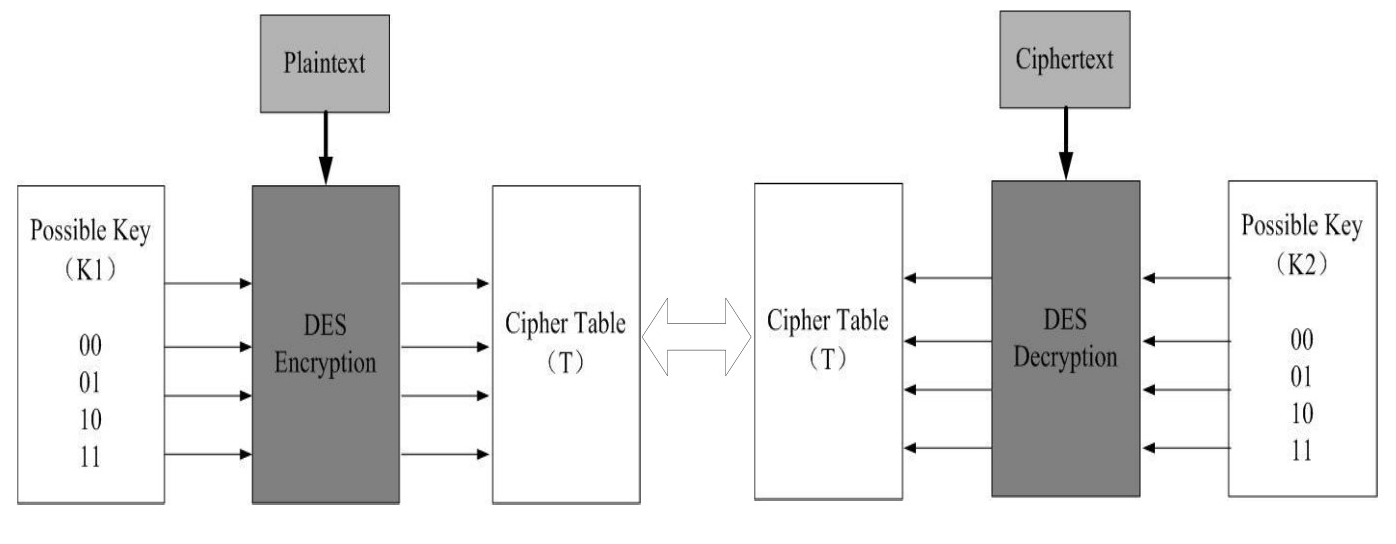
Triple DES

3DES with 3 keys (EDE-3)

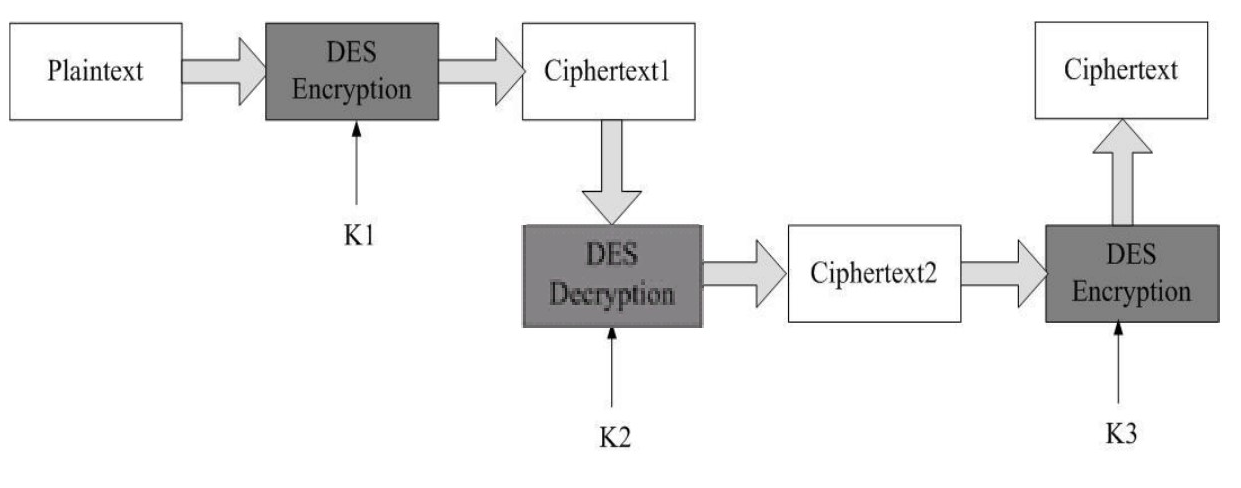
3DES with 2 keys (EDE-2)

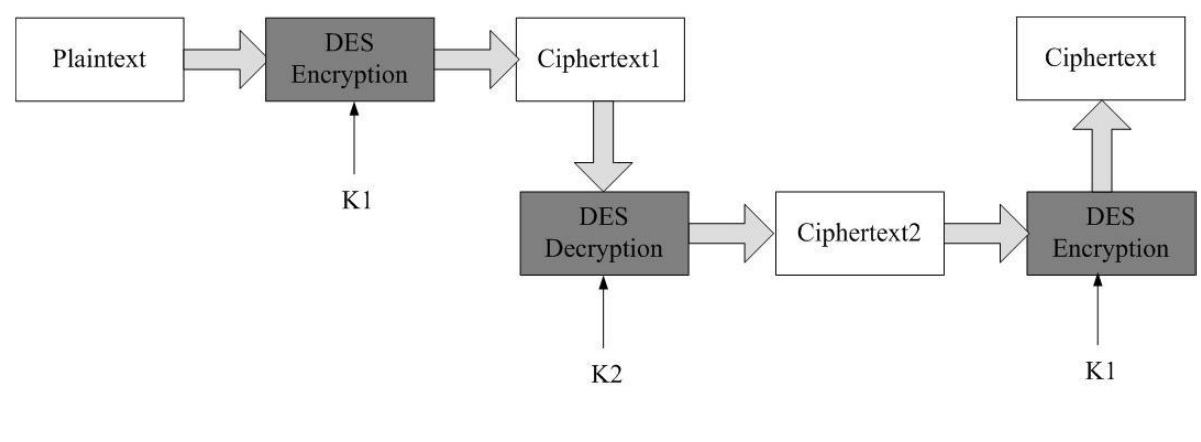
AES

Rijndael

• One of the fastest and strongest algorithms.
• Variable block length: 128, 192, 256 bits
• Variable key length: 128, 192, 256 bits
• Variable number of rounds (iterations): 10, 12, 14
• Number of rounds depend on key/block length
• The number of rounds \(N=max(N_k , N_b ) +6\)，where \(N_b\) is the block length and \(N_k\) is the key length, every 32bits is a unit

Rijndael structure

Rather than using just a substitution and a permutation at each stage like
DES, Rijndael consists of multiple cycles of Substitution, Shifting, Column
mixing and a KeyAdd operation

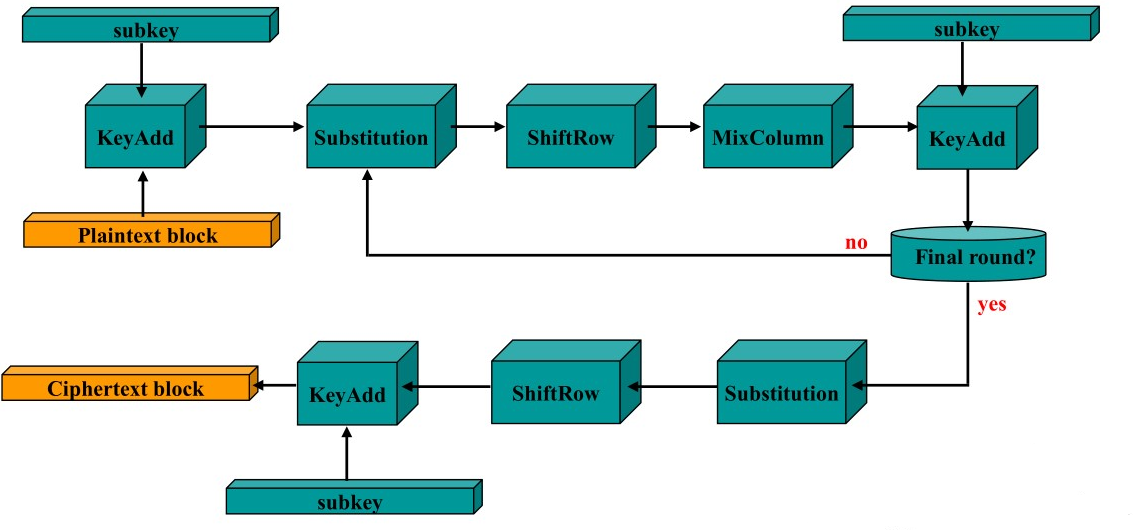
Note: 其中判断为从第一轮之后的新一轮开始就判断，因此开头生成一个subkey，循环流程N-2轮，生成N-2个subkey，最后一轮判断并进入最终一轮，生成一个subkey。

Encryption

• Key Schedule
  • The key is grouped into a column array and then expanded by adding 40 new columns
  • If the first four columns (given by the key) are C(0), C(1), C(2) and C(3), then the new columns are generated in a recursive（递归） manner
  • If i is not a multiple of 4 then column i is determined by: C(i) = C(i-4) XOR C(i-1)
  • If i is a multiple of 4 then column i is determined by:C(i) = C(i-4) XOR T(C(i-1))

Where T(C(i-1)) is a transformation of C(i-1) implemented as:

1. Cyclically shift (UP) the elements of C(i-1) by one byte
2. Use each of these 4 bytes as input into the S-box to create four new bytes e,f,g,h
3. Calculate a round constant r(i) = 2 (i-4)/4
4. Create the transformed column as: (e XOR r(i), f, g, h)
   The round key for the jth round consists of the columns C(4j), C(4j+1), C(4j+2), C(4j+3)