编译原理笔记

本科期间的编译原理笔记备份整理。

基本概念

编译与解释

编译：指把某种高级程序设计语言翻译成与之等价的具体计算机上的低级程序设计语言。

解释：将源语言书写的源程序作为输入，解释一句后就提交计算机执行一句，并不形成目标程序。

两者区别：前者有目标程序而后者无目标程序；前者运行效率高而后者便于人机对话。

编译结构

整个过程：源语言输入$\rightarrow$ 词法分析（自动机、正规文法）$\rightarrow$ 语法分析（LL（1）、LR（）、递归子程序）

$\rightarrow$ 语义分析（语义栈、属性文法）$\rightarrow$ 优化处理（DAG局部优化）$\rightarrow$ 目标代码生成$\rightarrow$ 目标语言输出

词法分析 -- 识别单词,确认词类;
语法分析 -- 识别短语和句型的语法属性；
语义分析 -- 确认单词、短语和句型的语义特征；
代码优化 -- 修辞、文本编辑；
代码生成 -- 生成译文。

形式语言

基本概念

形式语言：是字母表上的符号按一定的规则组成的所有符号串集合；其中的每个符号串称为一个句子。

字母表：元素(符号)的非空有限集合；

符号串：符号的有限序列；

符号串集合：有限个或者无限个符号串组成的集合；

规则：以某种形式表达的在一定范围内共同遵守的章程和制度；这里，指符号串的组成规则。

句型：由文法开始符号加推导出的任一符号串。

句子：由开始符号加推导出的任一终结符号串。

语法树：句型(句子)产生过程的一种树结构表示

符号串运算

所有集合运算都适用

正闭包：$A^+=A^1\cup A^2 \cup \cdots \cup A^n \cup \cdots$

星闭包：$A^*=A^0\cup A^1 \cup A^2 \cup \cdots \cup A^n \cup \cdots$

若 A 为任一字母表，则 A^* 就是该字母表上的所有符号串(包括空串)的集合。

文法

形式语言描述方法：枚举和文法

文法(grammar)是规则的有限集，表示为四元组：$G(Z)=(V_N,V_T,Z,P)$

$V_N$: 非终结符集 ( 定义的对象集，如：语法成分等 ) ；

$V_T$: 终结符集 ( 字母表 ) ；

$Z$: 开始符号 ( 研究范畴中最大的定义对象 ) ；

$P$: 规则集 ( 又称产生式集 ) ；

描述符号：$\rightarrow$ （生成）、$|$（或者）

文法符号：$Z,A\in V_N,\alpha,\beta\in (V_N\cup V_T)^*$

推导：从开始符号出发，对符号串中的定义对象，用其规则右部替换左部产生新的符号串，如此进行，直到新符号串中不再出现定义的对象为止，则最终的符号串就是一个句子。

标识符：指字母开头的字母、数字序列。

文法运算：直接推导、加推导、星推导

归约和推导过程是两个反向方向的过程，归约从符号串出发，推导从开始符号出发。

文法等价性：设$G_1$、$G_2$是两个文法，若$L(G_1)=L(G_2)$，则称$G_1$与$G_2$等价，记作$G_1\equiv G_2$；文法的等价性是指它们所定义的语言是一样的。

语法树

构造：

置树根为开始符号；
根据推导或归约产生产生式；
重复上述步骤直到推导或归约结束。

子树：由某一结点连同所有分支组成的部分。

简单子树：仅具有单层分支的子树。

任一子树的树叶全体(具有共同祖先的叶节点符号串)皆为短语；

任一简单子树的树叶全体(具有共同父亲的叶节点符号串)皆为简单短语；

一个句型的最左简单短语称为该句型的句柄。

递归文法

直接左递归文法：$S\rightarrow Sb|a$

直接右递归文法：$S\rightarrow bS|a$

递归文法是定义无限语言的工具，递归文法定义的语言有无限个句子

文法变换

删除无用产生式、删除$\epsilon$产生式、BNF表示法

删除不终结产生式算法：

构造能推导出终结符号串的非终结符集$V_{VT}$：
- 若有$A\rightarrow \alpha$ 且$\alpha \in V_T^*$ ；则令 $A\in V_{VT}$ ；
- 若有$A\rightarrow \beta$ 且$\beta \in (V_T+V_{VT})^*$ ；则令 $B\in V_{VT}$ ；
- 重复步骤上述步骤，直到$V_{VT}$不再扩大为止。
删除不在$V_{VT}$中的所有非终结符(连同其产生式)。

删除不可用产生式算法：

构造可用的非终结符集 $V_{US}:$
- 首先令 $Z\in V_{US}$ ; (Z 为文法开始符号)
- 若有$Z\rightarrow^{+} \cdots A \cdots，则令A\in V_{US}$
- 重复步骤上述步骤，直到$V_{US}$不再扩大为止。
删除不在$V_{US}$中的所有非终结符(连同其产生式)。

删除$\epsilon$产生式算法：

先构造可以推出空串的非终结符集：$V_{\epsilon}$
- 若$A\rightarrow \epsilon$，则令$A\in V_\epsilon$
- 若$B\rightarrow A_1 \cdots A_n$，则全部$A_i \in \epsilon$，故$B\in V_\epsilon$
- 重复上述步骤直到不再扩大
删除$A\rightarrow \epsilon$产生式
改写含A的B产生式，对其进行分裂

BNF表示法：比选项（）、可选项[]、重复项{}。

形式语言分类

0型文法：$\alpha \rightarrow \beta，\alpha \in (V_N\cup V_T)^*且至少有一个终结符，\beta \in (V_N\cup V_T)^*$

1型文法（上下文相关文法）：$\alpha A \beta \rightarrow \alpha u \beta，\alpha、\beta \in (V_N\cup V_T)^，u \in (V_N\cup V_T)^+$

2型文法（上下文无关文法）：$A \rightarrow \beta，A \in V_N，\beta \in (V_N\cup V_T)^*$

3型文法（正规文法）：$A\rightarrow aB 或 A\rightarrow a（右线性）；A\rightarrow Ba或A\rightarrow a（左线性） $

自动机

基本概念

有限自动机(Finite Automata) 被用来处理正规语言，后者是编译程序设计中词法分析的对象。

正规语言是指由正规文法定义的语言；程序设计语言中的单词，大都属于此种语言。

正规语言有三种等价的表示方法：正规文法、正规式、有限自动机

正规式是指由字母表中的符号，通过以下三种运算(也可以使用圆括号)连接起来构成的表达式 e：闭包、连接、或

有限自动机

有限自动机是一种数学模型，用于描述正规语言,可定义为五元组：$FA=(Q,\sum.S,F,\delta)$ ，状态集Q，字母表$\sum$，开始状态集$S$，结束状态集F，变换$\delta：\delta(i,j)=a$

两种表示：状态转换图、状态转换表

分类

确定有限状态机：开始状态唯一，变换函数单值，不带$\epsilon$边。

非确定有限状态机：不满足上述特征的

等价转换

自动机等价：设有两个有限自动机$FA_1$和$FA_2$，若$L(FA_1)= L(FA_2)$则称$FA_1$与$FA_2$等价，记作$FA1\equiv FA2$。

状态等价：设 i 和 j 为FA的两个状态，若把其看作初态，二者接受的符号串集合相同，则有 i $\equiv$j (等价)。

有限自动机的确定化
- 去除$\epsilon$边
  - 闭路合一
  - 标记隐含的开始态和结束态：开始态的$\epsilon$边通路节点加开始态+；结束态的$\epsilon$边逆向通路上节点加结束态-。
  - 删除$\epsilon$边，同时引入新边，凡是原来通路上发出的边，在其通路开始节点再发出
  - 重复上述步骤
- 确定化算法
  - 构造DFA变换表
  - 按照去$\epsilon$边的变换实施：$\delta({q_i^1,\cdots,q_i^n}，a_k)=\delta(q_i^1,a_k)\cup \cdots \cup (q_i^n,a_k)=\{q_j^1,cdots,q_j^n\}$
  - 若没有则添加新行
  - 重复上述步骤直到不增加
  - 标记含有开始态和结束态的行
有限自动机最小化
- 删除无用状态
  - 设 $q_0 $为开始态，则令 $q_0\in Q_{us} $；
  - 若 $q_i\in Q_{us}$且有 $\delta(q_i,a)= q_j $则令$ q_j\in Q_{us}$ ；
  - 重复上述步骤到不增加，之后删除所有不在其中的状态
- 删除等价状态
  - 分两个不等价集合结束态集合和非结束态集合
  - 把两个集合进一步划分不同子集，根据已划分的结果看变换的字母表是否相同
  - 重复步骤不增加
  - 合并每个子集的状态

词法分析

主要识别单词和翻译单词。

单词分类

标识符：用户给一些变量起的名字；

常数：以自身形态面对用户和系统；

特殊符：

关键字（系统内部定义，具有固定的意义，通常用来区分语法单元）
界符：单字符界符（+ - * / , ; : = < …）；双字符界符（ <= <> >= == `/* */ …）

识别单词

大多数编译程序使用“保留字”，即关键字不能用作标识符。系统预先造好关键字表，拼好的字符串，先查“关键字”表，查到了，视为关键字，否则，视为标识符。

词法分析中需要词法分析器和词法翻译器，可采用独立的方法或者子程序法

语法分析

定义：形式上说，语法分析是指对给定的符号串$\alpha$，判定其是否是某文法$G(Z)$的句子。

两种方法：推导法（自顶向下）、归约法（自顶向下）

递归子程序法

原理：对每一个非终结符，构造一个子程序，用以识别该非终结符所定义的符号串。每个子程序以产生式左部非终结符命名，以产生式右部构造子程序内容。

要求：具有相同左部的各产生式，首符号不同；文法不能有左递归（LL（1）要求）

构造算法：

扩展文法：增设一个产生式，作为主程序
入出口约定：子程序入口时，其首符号已经读来；子程序出口时，其后继符应该读来
子程序内容设计：终结符判定、确定后读下一个单词；非终结符调用、返回后不读下一单词；空串直接退出

LL（1）文法

LL(1)分析法是指从左到右扫描(第一个L) 、最左推导(第二个L)和只查看一个当前符号(括号中的1)之意；

LL(1)分析法又称预测分析法，属于自顶向下确定性语法分析方法。

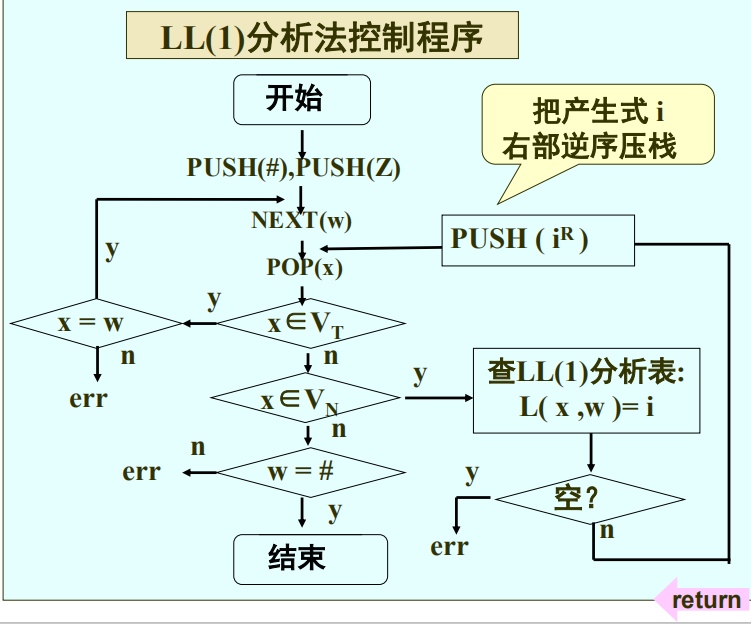
LL（1）分析法

利用一个分析栈（分析过程）、一个分析表（选择产生式）

分析栈：

#代表栈底符号和结束标记，开始
重复执行下面步骤：
- 若栈顶符=a，则当前符w=a，设有产生式$A\rightarrow a\alpha$，根据表POP，PUSH对应产生式
- 若栈顶符=a,当前符 w=a；则 POP,NEXT(w);
结束

分析表：根据select集进行绘制表

求文法选择集合，确认是否是 LL(1)文法；
一次取产生式：若 $A\rightarrow \alpha 序号$且$ a\in select(序号）$，则 $L( A , \alpha ) = i$

LL（1）文法判定

first($\alpha$)是从$\alpha$能够推导出的所有首符号。follow(A)是所有句型中紧跟在A之后出现的终结符。则：

$ first(\alpha)={t|\alpha\rightarrow^* t\cdots,t\in V_T} $

$ follow(\alpha)={t|Z\rightarrow^* \cdots At,t\in V_T} $

$ select(A\rightarrow\alpha)= \begin{cases} first(\alpha),a\not\rightarrow^* \epsilon \\\\ first(\alpha)\cup follow(A), a\rightarrow^* \epsilon \end{cases} $
注意：设 # 为输入串的结束符，则 #$\in$follow(Z);

针对$B\rightarrow \cdots A\beta$，求解follow集合：

$\beta$不为空：$first(\beta)\in follow(A)$
$\beta=\epsilon$：$follow(B)\in follow(A)$
$\beta$为空：$follow(B)\in follow(A)$

LL(1)文法是指文法中，具有相同左部的各产生式，其选择集合不相交

控制器设计

LR()分析法

LR( )分析法是指从左到右扫描(第一个 L) 、最左归约(最右推导的逆过程)(第二个 R)之意；它属于自底向上分析方法。常用的算法有LR(0)和LR(1)等，其中括号内的数是指无需查看(0)(或只需查看一个(1))当前符号，即可确定归约过程

LR()分析法与LL(1)分析法相比：

优点：对文法的限制少；分析速度快，能准确、即时地指出出错位置

缺点：分析器的构造工作量大，实现比较困难

关键问题

关键问题：确定句柄

句柄一定出现于某一个产生式的右部；是否是句柄，还要看其所在符号串中的位置。

LR(0)

产生式右部加连接符号$\cdot$

分类：

归约项目：$A\rightarrow \cdot$ ，产生式的右部已分析完；
移进项目：$A→\cdot a$，期待移进一个符号 a ；
待约项目：$A→\cdot B$，期待归约得到 B ；
接受项目：$S'→S\cdot$ ，整个句子分析完毕。

DFA状态：若干个LR(0)项目组成的集合，称为LR(0)项目集。

闭包函数closure( I )：I为一个LR(0)项目集，闭包算法如下：

$I\subseteq closure(I)$
如果$A\rightarrow \alpha \cdot B \beta \in closure(I)$，则$B\rightarrow r\in P$，则项目$b\rightarrow \cdot r\in closure(I)$
重复上述步骤直到不增加

状态转移函数$goto( I, X ) $:$goto( I, X )= closure( J )， J={A\rightarrow \alpha X \cdot B|A\rightarrow \alpha \cdot X B\in I}$

最后就是构造自动机作为句柄识别器

控制器设计

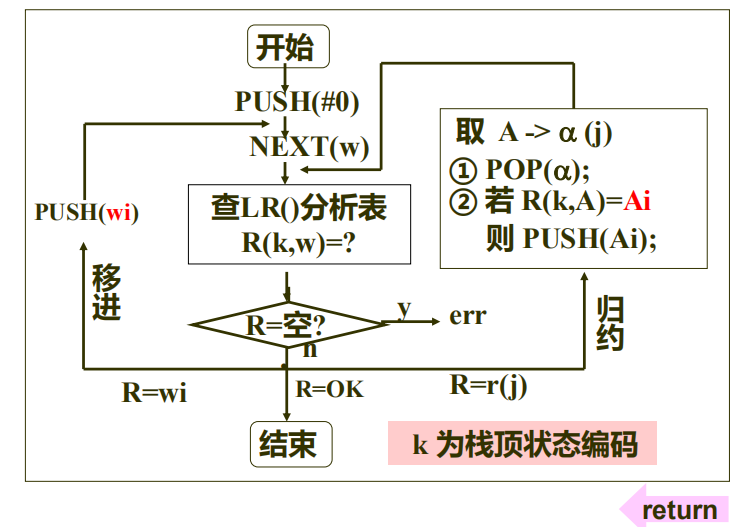
LR（0）分析

LR()分析表是 LR()分析法的知识表，是句柄识别器的一种机内表示形式；由于文法的内容和形式不同，导致求句的难易也不尽相同，于是出现了各种不同的LR()分析表。

满足下列条件的文法称为 LR(0)文法：每个项目集中，不存在移进项目和归约项目同时并存或多个归约项目同时并存；归约时不必查看当前输入符号

构造算法：

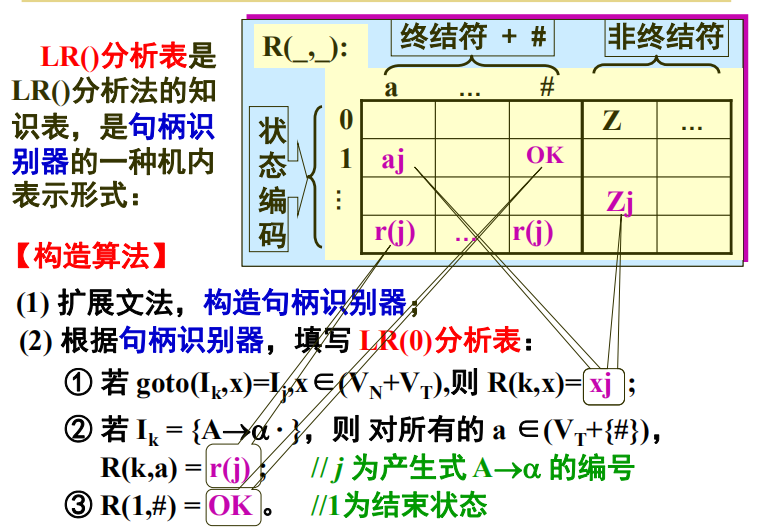
SLR(1)分析

SLR(1)分析器是 LR(0)分析器的改进与扩充；其中的 1 是指：当句柄识别器发生了移进和归约冲突或归约和归约冲突（移进归约冲突、归约归约冲突）时，通过查看1个当前符号就可解决。

其实就是在分析表的不同符号采用不同的goto内容

中间代码及翻译

语义分析过程：静态语义审查、中间代码生成

中间代码是高级程序语言中，各种语法成分的语义结构表示；它介于源语言和目标语言之间。

中间代码目的：

于进行与机器无关的代码优化；
使编译程序改变目标机更容易；
使编译程序的结构在逻辑上更为简单明确，以中间语言为界面，编译前端和后端的接口更清晰。

静态语义审查

作用：验证语法结构合法的程序是否真正有意义

包含内容：类型检查、控制流检查、一致性检查

中间代码

常见的形式

逆波兰式、四元式、三元式、语义树

四元式

基本形式：$(w,o_1, o_2,t)$，对应算符、对象1、对象2、结果

结构设计：赋值语句、转向语句、条件语句、循环语句

语法制导翻译

属性文法

属性文法是上下文无关文法在语义上的扩展，是一种接近形式化的语义描述方法，可定义为如下三元组：$A=(G,V,E)$，对应文法、属性集、语义规则集。

说明：属性代表与文法符号相关的信息，这里主要指语义信息(类型、种类、值和值地址…)；文法产生式中的每个文法符号都附有若干个这样的属性。属性可以进行计算和传递，语义规则就是在同一产生式中，相互关联的属性求值规则。

分类：综合属性（自底向上）、继承属性（自顶向下）

语法制导翻译技术

语法制导翻译(syntax_directed translations)是在语法分析过程中，随着分析(推导或归约)的逐步进展，每识别出一个语法结构，根据文法的每个规则所对应的语义子程序进行翻译的方法；核心技术是构造属性翻译文法，即在原文法产生式中插入语义动作符号(翻译子程序)，借以指明属性文法中属性求值时机和顺序。

语法制导翻译器实现

自顶向下属性翻译文法的要求：

原文法应满足自顶向下分析要求(如 LL(1)文法)；
属性是自顶向下可求值的；
动作符号可插入到产生式右部任何位置。

自底向上属性翻译文法的要求：

原文法应满足自底向上分析要求(如 LR( )文法)；
属性是自底向上可求值的；
动作符号只能位于产生式的最右端。

构造：根据递归子程序或根据分析表使用语义栈进行分析。分析表其实就是在语法分析表的基础上引入属性，在语义栈之中通过属性进行四元式生成

符号表组织

符号表是标识符的动态语义词典，属于编译中语义分析的知识库

主要内容：名字、类型（数据类型）、种类（语义角色）、地址

符号表：名字、类型、种类、地址

类型表：类码、指针

数组表：下界、上界、成分类型指针、成分类型长度

函数表：值单元、数据区、参数个数、参数表、入口地址

代码优化

优化分类：与机器无关的优化（全局、局部、循环）、与机器相关的优化

常见局部优化方法

常值表达式节省：先常数运算再将常数变量以常值替代
公共子表达式节省：找到公共表达式建立结果变量等价关系，等价变量以老变量替代新变量
删除无用赋值：确认一个变量两个赋值点间无引用点；前一赋值点为无用赋值
不变表达式外提
消除运算强度：

基本块及其划分

基本块是程序中一段顺序执行的语句序列，其中只有一个入口和一个出口。局部优化算法是以基本块为单位进行的，基本块也是目标代码生成的基本单位。

算法：

确定基本块入口语句：程序的第一个语句或转向语句转移到的语句；紧跟在转向语句后面的语句。
确定基本块的出口语句：下一个入口语句的前导语句；转向语句(包括转向语句本身)；停语句(包括停语句本身)

DAG局部优化

构造基本块内优化的 DAG
- 假设：$n_i$为已有结点号；n为新结点号；访问各结点信息时，按结点号逆序进行；
- 开始：DAG 置空；依次读取一四元式 $A=B\omega C$ ；分别定义 B , C 结点(若已定义过，则免)
- 若赋值四元式 $A=B$：把 A 附加于 B 上：若 A 在$n_2$已定义过，则删除其他结点上A的附加标记
- 若常值表达式$A=C_1\omega C_2 或 A=C_1$;：计算常值，如果常值已经在$n_1$定义过则附加标记，否则申请新结点；如果A在$n_2$已经定义过，则删除附加标记；
- 其他表达式$A = B\omega C 或 A=B：若在$ n_1 $存在公共表达式，则将其附加在$n_1$上；若不存在公共表达式，则申请新结点$n$；若 A 在 $n_2$ 已定义过，则删除之；
根据基本块内优化的 DAG，重组四元式
- 假设：临时变量的作用域是基本块内；非临时变量的作用域可以是基本块外。
- 开始：按结点编码顺序，依次读取每一结点 $n_1 $信息：
- 若 $n_1 $为带有附加标记的叶结点：若 $A_i $为非临时变量，则生成：$q1:A_i=B(i=1,2,\cdots)$
- 若$ n_1$ 为带有附加标记的非叶结点：生成 $q1: A=B\omega C$或生成$ q1: A=\omega B$；若非临时变量则生成常数表达式

目标代码及生成

目标代码生成是编译的最后一个阶段。

活跃变量：对于四元式$q(\omega \ B \ C \ A)$，B、C的应用点(q)，A的定义点(q)，一个变量从某时刻(q)起，到下一个定义点止，其间若有应用点，则称该变量在q是活跃的(y)，否则称该变量在q是非活跃的(n)。

临时变量在基本块出口后是非活跃的(n)；非临时变量在基本块出口后是活跃的(y)。

基本问题

寄存器分配问题：

置描述表，记录寄存器和变量的当前状态
寄存器分配规则：主动释放、选空闲者、强迫释放

目标代码生成问题：

基本块开始时所有寄存器应是空闲的；基本块结束时应释放所占用的寄存器。
一个变量被赋值时，要分配一个寄存器保留其值，并且要填写相应的描述表。
为了生成高效的目标代码，生成算法中要引用寄存器的分配原则和变量的活跃信息。

代码生成器设计

指令： (op R, M)

RDV：寄存器状态变量（0，X）

BACK(pi,.pj)：返填函数

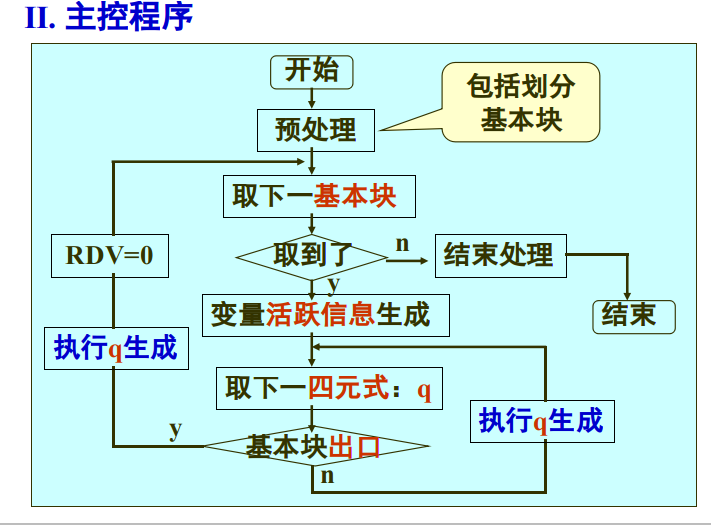
单个四元式生成要点：

表达式四元式$(\omega \ B \ C \ A)$：释放寄存器，编运算指令，A不存储但登记在RDV中！
赋值四元式$(= \ B \ _ \ A)$：编取B(B在R中则免，否则释放寄存器)、存A指令！
转向四元式$(do \ B \ \_ \ \_)$：释放寄存器，编转向指令，保存该地址于SEM栈中！

释放寄存器：编存储指令，保存占有寄存器的活跃变量值；通常发生在如下两个时刻：为结果变量申请寄存器时、基本块出口时

生成器分两类：单寄存器型和多寄存器型，区别在于寄存器的使用数量与用法。

表达式目标代码生成

基本块内活跃信息求解

posted @ 2022-05-05 17:17 FrancisQiu 阅读(497) 评论(0) 收藏举报

刷新页面返回顶部

道隐于小成，言隐于荣华

FrancisQiu's cnblog

backup blogs from former blog site.

编译原理笔记

基本概念

编译与解释

编译结构

形式语言

基本概念

符号串运算

文法

语法树

递归文法

文法变换

形式语言分类

自动机

基本概念

有限自动机

分类

等价转换

词法分析

单词分类

识别单词

语法分析

递归子程序法

LL（1）文法

LL（1）分析法

LL（1）文法判定

控制器设计

LR()分析法

关键问题

LR(0)

控制器设计

LR（0）分析

SLR(1)分析

中间代码及翻译

静态语义审查

中间代码

常见的形式

四元式

语法制导翻译

属性文法

语法制导翻译技术

语法制导翻译器实现

符号表组织

代码优化

常见局部优化方法

基本块及其划分

DAG局部优化

目标代码及生成

基本问题

代码生成器设计

表达式目标代码生成

基本块内活跃信息求解

公告