离散数学中矩阵乘法的法则

乘法运算：两个矩阵要可以相乘，必须是A矩阵的列数B矩阵的行数相等，才可以进行乘法，矩阵乘法的原则是，A矩阵的第i行中的元素分别与B矩阵中的第j列中的元素相乘再求和，得到的结果就是新矩阵的第i行第j列的值。

除法运算：一般不说矩阵的除法。都是讲的矩阵求逆。

 

 

 

 

 

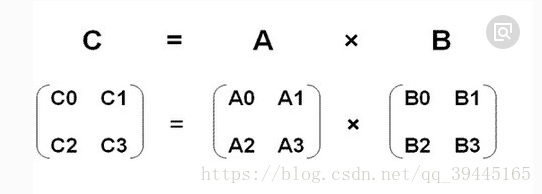
矩阵乘法的结果为行与列的关系为：行数量为A的行数量， 列数量为B的列数量

 

因为每一次都是A的行与B的列，所以最外层的两层循环可以使用A的行的数量的变化，B的列的数量进行变化

而最里面的循环可以是A的列或者是B的行来进行变化，因为A的列和是B的行数量是相等的，这样就可以使用三层循环来解决，代码如下：

public class Main {
    public static void main(String[] args) {
        int matrixA[][] ={
            {1, 1},
            {1, 1}
        }; 
        int matrixB[][] = {
            {1, 1},
            {1, 1}
        }; 
        int matrix[][] = matrixMultiple(matrixA, matrixB);
        print(matrix);
    }
 
    private static void print(int[][] matrix) {
        for(int i = 0; i < matrix.length; i++){
            for(int j = 0; j < matrix[0].length; j++){
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }    
    }
 
    private static int[][] matrixMultiple(int[][] matrixA, int[][] matrixB) {
        int res[][] = new int[matrixA.length][matrixB[0].length];
        for(int i = 0; i < matrixA.length; i++){
            for(int j = 0; j < matrixB[0].length; j++){
                for(int k = 0; k < matrixA[0].length; k++){
                    res[i][j] += matrixA[i][k] * matrixB[k][j];
                }
            }
        }
        return res;
    }
}

 

 

转： https://jingyan.baidu.com/article/95c9d20d6a8b06ad4f756124.html

 

https://baike.baidu.com/item/%E7%9F%A9%E9%98%B5%E4%B9%98%E6%B3%95/5446029

https://blog.csdn.net/qq_39445165/article/details/82347059

https://www.cnblogs.com/fps2tao/p/16707980.html