最大子数组和-leetcode

题目描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

解法一

思路：

采用动态规划的思想，sum[i]表示以i为结尾的最大子数组和。当新增加一个数时，此时的sum[i+1]分为两种情况，第一种就是sum[i]+nums[i+1]>=nums[i]（简化sum[i]>=0），说明前面以i+1为结尾的最大子数组为之前以i为结尾的子数组加上新加入的元素，第二种情况，sum[i]+nums[i+1]<nums[i]，说明前面以i+1为结尾的最大子数组为单独的新加入元素。记录所出现的最大子数组和。

代码：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;

public class leetcode_013 {

    public static int maxSubArray(int[] nums) {
        int sum=nums[0];
        int maxSum=sum;
        if(nums.length==1)return nums[0];
        int cnt=1;
        int numsLen=nums.length;
        while(cnt<numsLen){
            if(sum>=0){
                sum+=nums[cnt];
                maxSum=maxSum<sum?sum:maxSum;
            }else {
                sum = nums[cnt];
                maxSum=maxSum<sum?sum:maxSum;
            }
            cnt++;
        }
        return maxSum;
    }


    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String[] line = sc.nextLine().split(",");
        int[] nums= Arrays.stream(line).mapToInt(Integer::parseInt).toArray();
        int res =maxSubArray(nums);
        System.out.println(res);
    }
}

解法二

思路：

来自官方分治思想。

我们定义一个操作 get(a, l, r) 表示查询 a 序列 [l,r] 区间内的最大子段和，那么最终我们要求的答案就是 get(nums, 0, nums.size() - 1)。如何分治实现这个操作呢？对于一个区间 [l,r]，我们取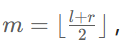，对区间[l,m]和 [m+1,r] 分治求解。当递归逐层深入直到区间长度缩小为 1 的时候，递归「开始回升」。这个时候我们考虑如何通过[l,m]区间的信息和 [m+1,r] 区间的信息合并成区间 [l,r] 的信息。

对于一个区间[l,r]，我们可以维护四个量：

• lSum 表示 [l,r] 内以 l 为左端点的最大子段和
• rSum 表示 [l,r] 内以 r 为右端点的最大子段和
• mSum 表示 [l,r] 内的最大子段和
• iSum 表示 [l,r] 的区间和

以下简称 [l,m] 为 [l,r] 的「左子区间」，[m+1,r] 为[l,r]的「右子区间」。我们考虑如何维护这些量呢（如何通过左右子区间的信息合并得到 [l,r] 的信息）？对于长度为 1 的区间 [i,i]，四个量的值都和nums[i]相等。对于长度大于 1 的区间：

首先最好维护的是 iSum，区间 [l,r] 的 iSum 就等于「左子区间」的 iSum 加上「右子区间」的 iSum。
对于 [l,r] 的 lSum，存在两种可能，它要么等于「左子区间」的 lSum，要么等于「左子区间」的 iSum 加上「右子区间」的 lSum，二者取大。
对于 [l,r] 的 rSum，同理，它要么等于「右子区间」的 rSum，要么等于「右子区间」的 iSum 加上「左子区间」的 rSum，二者取大。
当计算好上面的三个量之后，就很好计算 [l,r] 的mSum 了。我们可以考虑 [l,r] 的mSum 对应的区间是否跨越 m——它可能不跨越 m，也就是说[l,r]的mSum可能是「左子区间」的mSum和 「右子区间」的 mSum 中的一个；它也可能跨越 m，可能是「左子区间」的 rSum 和 「右子区间」的lSum求和。三者取大。

这样问题就得到了解决。

代码：

class Solution {
    public class Status {
        public int lSum, rSum, mSum, iSum;

        public Status(int lSum, int rSum, int mSum, int iSum) {
            this.lSum = lSum;
            this.rSum = rSum;
            this.mSum = mSum;
            this.iSum = iSum;
        }
    }

    public int maxSubArray(int[] nums) {
        return getInfo(nums, 0, nums.length - 1).mSum;
    }

    public Status getInfo(int[] a, int l, int r) {
        if (l == r) {
            return new Status(a[l], a[l], a[l], a[l]);
        }
        int m = (l + r) >> 1;
        Status lSub = getInfo(a, l, m);
        Status rSub = getInfo(a, m + 1, r);
        return pushUp(lSub, rSub);
    }

    public Status pushUp(Status l, Status r) {
        int iSum = l.iSum + r.iSum;
        int lSum = Math.max(l.lSum, l.iSum + r.lSum);
        int rSum = Math.max(r.rSum, r.iSum + l.rSum);
        int mSum = Math.max(Math.max(l.mSum, r.mSum), l.rSum + r.lSum);
        return new Status(lSum, rSum, mSum, iSum);
    }
}