二叉树

二叉树

题目描述

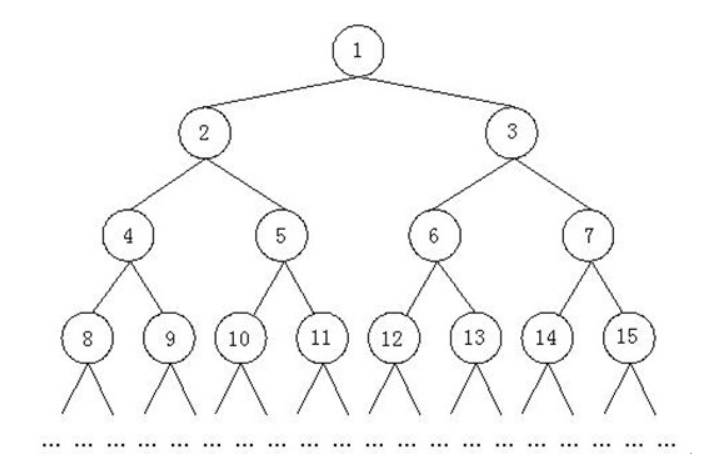
​ 如上所示，由正整数1，2，3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是，结点m所在的子树中一共包括多少个结点。

​ 比如，n = 12，m = 3那么上图中的结点13，14，15以及后面的结点都是不存在的，结点m所在子树中包括的结点有3，6，7，12，因此结点m的所在子树中共有4个结点。

输入格式

输入数据包括多行，每行给出一组测试数据，包括两个整数m，n (1 <= m <= n <= 1000000000)。最后一组测试数据中包括两个0，表示输入的结束，这组数据不用处理。

输出格式

对于每一组测试数据，输出一行，该行包含一个整数，给出结点m所在子树中包括的结点的数目。

样例输入

3 7
142 6574
2 754
0 0

样例输出

3
63
498

解题思路

m---为当前层的起点，s---为当前层的节点数，end---当前层的结束节点编号，2m则为下一层的新的起点，2s为下一层的节点数。

1. 若end<=n,那么当前层所有节点数都需要计入节点总数。
2. 若end>n,那么当前层的节点数需要将取n编号前的节点数，同时需要包括n节点。

代码

import java.util.ArrayList;
import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        ArrayList<Integer> nlist = new ArrayList<>();
        ArrayList<Integer> mlist = new ArrayList<>();
        int m = scanner.nextInt();
        //读取输入的数据
        while(m!=0)
        {
            mlist.add(m);
            int n = scanner.nextInt();
            nlist.add(n);
            m=scanner.nextInt();
        }
        for(int i=0;i<nlist.size();i++){
           int res=countNodes(mlist.get(i),nlist.get(i));
            System.out.println(res);
        }
    }
    public static int countNodes(int m, int n) {
        if (m > n) {
            return 0;
        }
        int count = 0;
        long currentLevelStart = m;
        long currentLevelCount = 1;

        while (currentLevelStart <= n) {
            long index_end = currentLevelStart + currentLevelCount - 1;
            if ( index_end> n) {
                count += (n - currentLevelStart + 1);
            } else {
                count += currentLevelCount;
            }

            // 检查是否可能溢出，避免无限循环
            if (currentLevelStart > Long.MAX_VALUE / 2) {
                break;
            }

            currentLevelStart *= 2;
            currentLevelCount *= 2;
        }

        return count;
    }
}