沙子合并

沙子合并

题目描述

设有N堆沙子排成一排，其编号为1，2，3，…，N（N< =300）。每堆沙子有一定的数量，可以用一个整数来描述，现在要将这N堆沙子合并成为一堆，每次只能合并相邻的两堆，合并的代价为这两堆沙子的数量之和，合并后与这两堆沙子相邻的沙子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同，如有4堆沙子分别为 1 3 5 2 我们可以先合并1、2堆，代价为4，得到4 5 2 又合并 1，2堆，代价为9，得到9 2 ，再合并得到11，总代价为4+9+11=24，如果第二步是先合并2，3堆，则代价为7，得到4 7，最后一次合并代价为11，总代价为4+7+11=22；问题是：找出一种合理的方法，使总的代价最小。输出最小代价。

输入格式

第一行一个数N表示沙子的堆数N。 第二行N个数，表示每堆沙子的质量。 < =1000

输出格式

合并的最小代价

样例输入

4
1 3 5 2

样例输出

22

解题思路

采用动态规划的方法。

设 dp[i][j] 表示合并第 i 到第 j 堆沙子的最小代价。

状态转移方程

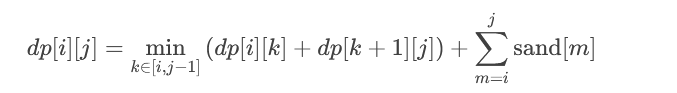
其中，k 为分割点，将区间 [i, j] 分成 [i, k] 和 [k+1, j]，分别计算两部分的合并代价，再加上合并后的总重量。

代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        int[] sand = new int[N + 1];
        int[] sum = new int[N + 1];
        for (int i = 1; i <= N; i++) {
            sand[i] = scanner.nextInt();
            sum[i] = sum[i - 1] + sand[i];
        }

        int[][] dp = new int[N + 1][N + 1];
        for (int len = 2; len <= N; len++) { // 区间长度
            for (int i = 1; i + len - 1 <= N; i++) { // 区间起点
                int j = i + len - 1; // 区间终点
                dp[i][j] = Integer.MAX_VALUE;
                for (int k = i; k < j; k++) { // 分割点
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]);
                }
            }
        }

        System.out.println(dp[1][N]);
    }
}

注意事项

dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]);其中sum[j]-sum[i-1]表示的是从i到j沙子堆的重量总和，sum[i]表示的是前i堆的重要之和，sum[j]就是前j堆的重量，sum[i-1]就是前i-1堆的重量，两者相减就是i到j堆的重量。

贪心算法局限性

贪心算法存在局限性，只能得到局部最优解，不能得到全局最优解。

例子

考虑四堆沙子 [3, 4, 2, 5]：

• 贪心策略：
  1. 合并 4 和 2（代价 6），得到 [3, 6, 5]。
  2. 合并 3 和 6（代价 9），得到 [9, 5]。
  3. 合并 9 和 5（代价 14），总代价为 6 + 9 + 14 = 29。
• 最优策略：
  1. 合并 3 和 4（代价 7），得到 [7, 2, 5]。
  2. 合并 2 和 5（代价 7），得到 [7, 7]。
  3. 合并 7 和 7（代价 14），总代价为 7 + 7 + 14 = 28。
• 贪心算法得到的总代价更高，说明局部最优无法保证全局最优。