CF1824D
我们定义\(f(l,r,x)=\sum_{j=1}^{x}{\sum_{i=l}^{\min{(j,r)}}{g(i,j)}}\),容易发现对于一个询问的答案\(ans = f(l,r,y)-f(l,r,x-1)\)
我们扫描先维护右端点\(r\)从左向右移动,线段树下标\(i\)上的值维护的是\(g(i,r)\)
我们考虑再维护一个01数组\(b_i\),表示\(a_i\)这个数是否是在\([i,r]\)中第一次出现。每次移动右端点时把当前位置戳成\(1\),把上一个和该元素相同的位置戳成\(0\)。
我们发现\(g(i,r)\)就等于\(i\)之后第一个\(b_i=1\)的下标。接下来我们考虑加入\(a_r\)后会对哪些答案产生贡献
在修改之前的局面(图盗自:这里)
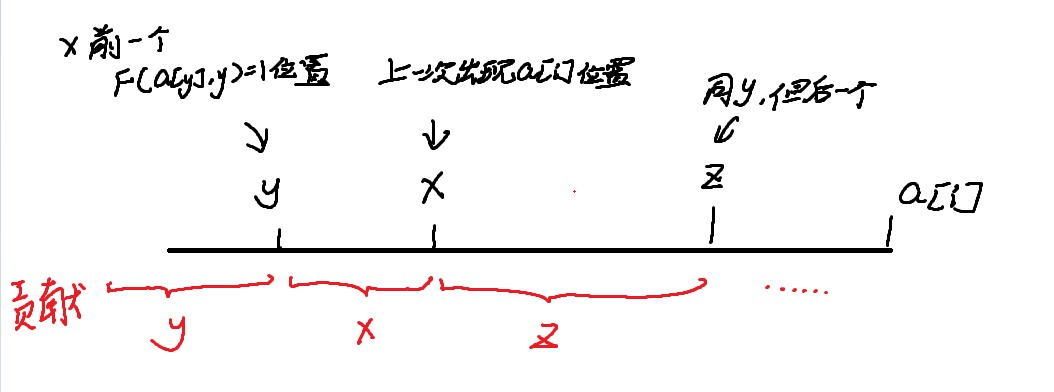
我们发现加入\(a_i\)后图中\(b_x\)从\(1 \rightarrow 0\),这会让区间\([y+1,x]\)内的值变成\(z\),然后让\([k+1,i]\)这个位置的值覆盖成\(i\)(如下图)
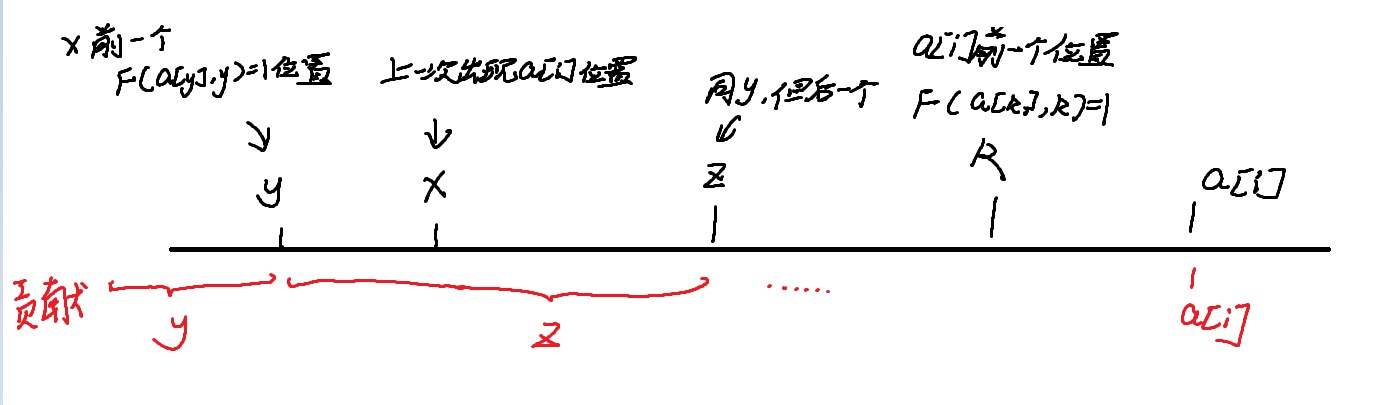
但由于这题很卡常,我们可以发现如果\(a_{i-1} \neq a_i\),则\(k=i-1\);而如果\(a_{i-1} = a_i\),则\(x=i-1,z=i\)。因此我们对于第二种修改只需要修改位置\(i\)的值为\(i\)即可
找到这些位置我们可以用\(set\)维护\(b_i=1\)的位置,并通过在\(set\)中二分和移动迭代器来查找到图中的\(y,x,z\)
而我们要找的答案即为右端点\(r=1 \rightarrow x\)的过程中所有区间\([l,r]\)的和
但这只是一个询问的情况,我们发现如果有\(Q\)个询问这么做显然是\(O(Qn\log n)\)的,是无法通过的
但我们发现我们实际上维护了这\(Q\)次询问的答案,只是我们要考虑如何快速的把他们累加
看一眼线段树3,我们发现这个“历史和”很符合我们的要求
于是我们只需要把所有询问离线,把\(x,y\)拆成\(\{l,r,x-1\}\)和\(\{l,r,y\}\),线段树维护以下操作:
-
区间赋值
-
查询区间历史和
以下说一下怎么维护区间赋值历史区间和线段树,会的可以走了
首先建一棵线段树
朴素的,我们先维护题目要求的\(lazytag\):设对这个区间的历史区间和更新了\(hs\)次,把当前区间覆盖成了\(cov\)。然后考虑怎么写\(pushdown\)函数
我们显然需要现进行\(hs\)标记的下传再下传\(cov\),因为如果我们先下传\(cov\),我们就把原来的历史信息覆盖掉了,就无法知道在修改前\(hs\)对历史区间和的贡献
我们发现这个是不太好维护的,这里引用一个大佬的博客,这里这个队列的形容是很贴切的
我们发现如果当前区间的队列中有\(hs\)和\(cov\),这时加入了一个\(hs'\),我们是无法直接累加到\(hs\)中的,因为中间隔着\(cov\)影响到了\(hs\)的贡献
但我们发现如果有了\(cov\)操作,我们之后的\(hs\)标记不就是加上了一个常数吗!于是我们只需要再维护一个当前历史区间和加上的常数\(cst\)即可
这时如果队列中有\(hs\),\(cst\),\(cov\),进入了\(hs'\),我们就可以把\(hs'\)和\(cov\)合并,\(cst \leftarrow cst + hs' \times cov\)即可
然后注意标记下传的顺序,\(hs\)必须在\(cov\)的前面
最终复杂度\(O(n\log n + Q\log n)\)
\(p.s.2023/9/19\),看了P8868发现自己对这类题的思路多少有点出入
这道题他左端点的范围是固定的,而比赛这题左端点范围不固定。因此理论上我们应该维护右端点递增的历史区间和,而这个貌似是不可做的
但比赛这题和这题做法类似的原因是:如果一个\(l>r\),则\(l\)的值不会被修改,及即使多算了\(l\)的答案也不会对最终答案产生影响,因为他没有被更新,所以贡献为\(0\)
代码:
#include <bits/stdc++.h>
// #pragma GCC optimize(2)
#define pcn putchar('\n')
#define ll long long
#define MP make_pair
#define fi first
#define se second
#define gsize(x) ((int)(x).size())
#define Min(a, b) (a = min(a, b))
#define Max(a, b) (a = max(a, b))
#define For(i, j, k) for(int i = (j), END##i = (k); i <= END##i; ++ i)
#define For__(i, j, k) for(int i = (j), END##i = (k); i >= END##i; -- i)
#define Fore(i, j, k) for(int i = (j); i; i = (k))
//#define random(l, r) ((ll)(rnd() % (r - l + 1)) + l)
using namespace std;
namespace IO {
template <typename T> inline T read(T &num){
num = 0; T f = 1; char c = ' '; while(c < '0' || c > '9') if((c = getchar()) == '-') f = -1;
while(c >= '0' && c <= '9') num = (num << 1) + (num << 3) + (c ^ 48), c = getchar();
return num *= f;
}
template <typename T> inline void Write(T x){
if(x < 0) putchar('-'), x = -x; if(x == 0){putchar('0'); return ;}
if(x > 9) Write(x / 10); putchar(x % 10 + '0'); return ;
}
inline void putc(string s){ int len = s.size() - 1; For(i, 0, len) putchar(s[ i ]); }
template <typename T> inline void write(T x, string s = "\0"){ Write( x ), putc( s ); }
}
using namespace IO;
/* ====================================== */
const int maxn = 1e6 + 50;
const ll INF = (1ll << 60);
int n, Q;
int a[ maxn ];
int buc[ maxn ];// 记录上一个和自己数字相同的位置
set<int> s;// 记录每个数字最后出现的位置
struct Ask{
int l, r, x, id, k;
bool operator < (const Ask &y) const{
return (x ^ y.x ? x < y.x : k < y.k);
}
} ask[ maxn << 1 ];
ll ans[ maxn ];
struct SegmentTree{
#define ls (p << 1)
#define rs (p << 1 | 1)
struct Tree{
ll hs, sum;// 历史区间和;区间和
Tree operator + (const Tree &y) const{
Tree res;
res.hs = hs + y.hs;
res.sum = sum + y.sum;
return res;
}
} tr[ maxn << 2 ];
struct Tag{
ll hs, cst, cov;
//hs:对当前区间维护历史区间和的次数
//cst:当前这个区间加上的常数(为了合并hs和cov的临时懒标记)
//cov:对当前区间的覆盖tag
} tag[ maxn << 2 ];
inline void PushUp(int p){
tr[ p ] = tr[ ls ] + tr[ rs ];
}
inline void SmlUpd(int l, int r, Tag k, int p){
if(k.hs){//如果这个区间维护了k.hs次历史区间和
tr[ p ].hs += k.hs * tr[ p ].sum;//会让历史区间和加上k.hs个区间和
if(tag[ p ].cov) tag[ p ].cst += k.hs * tag[ p ].cov;//如果当前区间被覆盖,那我们不用管原来区间和,历史区间和就弱化成了常数
else tag[ p ].hs += k.hs;//否则就加到历史区间和的tag中
}
if(k.cst){//如果这个区间有常数
tr[ p ].hs += k.cst * (r - l + 1);//让历史区间和加上常数
tag[ p ].cst += k.cst;//常数也要累加
}
if(k.cov){//如果这个区间有覆盖
tr[ p ].sum = k.cov * (r - l + 1);
tag[ p ].cov = k.cov;
}
//操作顺序非常重要,必须是k.hs在k.cov前面,因为k.hs维护的显然是在区间覆盖之前的历史区间和
//因为如果覆盖后才开始统计历史区间和,我们会直接把历史区间和加到常数里,而不是历史区间和
//而如果我们先进行k.cov操作,我们就丢失了在没覆盖之前维护的值,这样是错误的
}
inline void PushDown(int l, int r, int p){
if(!tag[ p ].cov && !tag[ p ].cst && !tag[ p ].hs) return ;
int mid = l + r >> 1;
SmlUpd(l, mid, tag[ p ], ls);
SmlUpd(mid + 1, r, tag[ p ], rs);
tag[ p ] = Tag{0, 0, 0};
}
inline void modify(int l, int r, int x, int y, ll k, int opt, int p){
if(x <= l && r <= y){
if(opt == 1) SmlUpd(l, r, Tag{0, 0, k}, p);
else SmlUpd(l, r, Tag{k, 0, 0}, p);
return ;
}
PushDown(l, r, p);
int mid = l + r >> 1;
if(x <= mid) modify(l, mid, x, y, k, opt, ls);
if(mid < y) modify(mid + 1, r, x, y, k, opt, rs);
PushUp(p);
}
inline ll query(int l, int r, int x, int y, int p){
if(x <= l && r <= y) return tr[ p ].hs;
PushDown(l, r, p);
int mid = l + r >> 1;
ll res = 0;
if(x <= mid) res = query(l, mid, x, y, ls);
if(mid < y) res += query(mid + 1, r, x, y, rs);
return res;
}
inline void modify(int l, int r, ll k, int opt){
modify(1, n, l, r, k, opt, 1);
}
inline ll query(int l, int r){
return query(1, n, l, r, 1);
}
#undef ls
#undef rs
} seg;
inline void mian(){
read(n), read(Q);
For(i, 1, n) read(a[ i ]);
int l, r, x, y, cntq = 0;
For(i, 1, Q){
read(l), read(r), read(x), read(y);
ask[ ++ cntq ] = Ask{l, min(r, x - 1), x - 1, i, -1};
ask[ ++ cntq ] = Ask{l, min(r, y), y, i, 1};
// 卡常题,把r和x取min防卡常
}
sort(ask + 1, ask + (Q << 1) + 1);
s.insert(0);
r = 1;
For(i, 1, Q << 1){
if(ask[ i ].l > ask[ i ].r) continue;// 卡常卡常卡常卡常
while(r <= ask[ i ].x){
int pre = buc[ a[ r ] ];
if(pre){
auto it = s.find(pre);
l = *(-- it); ++ it;
x = ((++ it) == s.end() ? r : *it); -- it;
//找到会影响的区间
seg.modify(l + 1, pre, x, 1);
s.erase(it);
}
buc[ a[ r ] ] = r;
s.insert(r);
seg.modify(r, r, r, 1); //同样找到会影响的区间
seg.modify(1, n, 1, 2); //更新历史区间和
++ r;
}
ans[ ask[ i ].id ] += seg.query(ask[ i ].l, ask[ i ].r) * ask[ i ].k;
}
For(i, 1, Q) write(ans[ i ], "\n");
}
inline void init(){
}
int main() {
#ifdef ONLINE_JUDGE
#else
freopen("data.in", "r", stdin);
// freopen("data.out", "w", stdout);
#endif
int T = 1;
while(T --){
init();
mian();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号