Educational Codeforces Round 120 (Rated for Div. 2) A - D

A - Construct a Rectangle

题意：
给你\(3\)个数\(l_1,l_2,l_3\)，问能否分割其中一个数，使得四个数组成一个矩形，特殊地，正方形也是矩形。

• 判段一下是否有两数之和等于另一数后者是否有两数相等且第三个数为偶数

#include <bits/stdc++.h>

using namespace std;

void solve() {
	int l1,l2,l3; cin >> l1 >> l2 >> l3;
	if(l1 + l2 == l3 || l1 + l3 == l2 || l2 + l3 == l1) {
		cout << "YES\n";
	} else if(l1 == l2 && l3 % 2 == 0|| l1 == l3 && l2 % 2 == 0|| l2 == l3 && l1 % 2 == 0) {
		cout << "YES\n";
	} else {
		cout << "NO\n";
	}
}

int main() {
	int T; cin >> T;
	while(T --) {
		solve();
	}
}

B - Berland Music

题意：
给定排列\(p\)和一个二进制\(01\)串\(s\)，构造一个排列\(q\)使得二进制串中\(\forall s_i = 1,s_j = 0,q_i > q_j\)，并且要求\(\sum_{i = 1}^n|q_i - p_i|\)最小。

• 贪心
• 首先根据\(01\)串把\(1 - n\)分为两大类，小的分配给串中为\(0\)的位置，大的反之，对应的分配规则即按照原先\(p\)中大小关系分配给对应大小关系的\(q\)使得差尽可能的小。

#include <bits/stdc++.h>

using namespace std;

void solve() {
	int n; cin >> n;
	vector<int>p(n + 1),q(n + 1);
	for(int i = 1;i <= n;i ++) {
		cin >> p[i];
	}
	vector<pair<int,int>>a1,a0;
	string s; cin >> s;
	for(int i = 0;i < s.size();i ++) {
		if(s[i] == '1')
			a1.push_back({p[i + 1],i + 1});
		else 
			a0.push_back({p[i + 1],i + 1});
	}
	sort(a1.begin(),a1.end());
	sort(a0.begin(),a0.end());
	int pos = 0;
	for(auto i : a0) {
		q[i.second] = ++pos;
	};
	for(auto i : a1) {
		q[i.second] = ++pos;
	}
	for(int i = 1;i <= n;i ++) {
		cout << q[i] << " \n"[i == n];
	}
}

int main() {
	int T; cin >> T;
	while(T --) {
		solve();
	}
	return 0;
}

C - Set or Decrease

题意：
给定一个数列\(a\)和一个数\(k\)。每次操作你可以选择如下两种操作之一：

• 选择一个位置\(i\)，使得\(a_i = a_i + 1\)
• 选择两个位置\(i,j\)，使得\(a_i = a_j\)

问需要最少的操作次数使得\(\sum a \le k\)

• 根据题目所给样例我们也能贪心的想到，更优的方案是摁住数列中最小的数减一定次数后，再把数列中剩余大的数一起减到当前最小数的值
• 将数组排序后，维护一个后缀后，方便每次统计答案
• 二分操作次数，每次\(check\)时，因为\(k\)很大，我们不能枚举最小数减多少次，我们直接枚举后缀的几个数变小，剩下的次数直接让最小的\(a\)减去即可
• 注意枚举的边界，因为我们默认用\(a_1\)进行减操作，所以只需枚举\(0 - n - 1\)的后缀和即可，其实也易得变\(a_1\)肯定不是最好的操作
• 复杂度\(O(nlogn)\)

#include <bits/stdc++.h>

using namespace std;
//1 1 1 2 2 3 6 6 8 10

void solve() {
	int n; long long k; 
	cin >> n >> k;
	vector<long long>a(n + 1),s(n + 2,0);
	for(int i = 1;i <= n;i ++) cin >> a[i];
	sort(a.begin() + 1,a.begin() + 1 + n);
	for(int i = n;i >= 1;i --) s[i] = s[i + 1] + a[i];
	if(s[1] <= k) {
		cout << "0\n";
	} else if(n == 1) {
		cout << a[1] - k << '\n';
	} else {
		auto check = [&](long long x) {
			for(int i = 0;i < n && i <= x;i ++) {//枚举把后缀的几个数变掉 这么写不要带n因为默认了第一个是用来减的 不过也易得 先减再变肯定比直接变好
				long long t = a[1] - (x - i);
				long long del = s[n - i + 1] - (t * i) + (x - i);
				if(s[1] - k <= del)
					return true;
			}
			return false;
		};
		long long l = 1,r = s[1] - k,ans;
		while(l <= r) {
			long long mid = l + r >> 1;
			if(check(mid)) {
				r = mid - 1; ans = mid;
			} else {
				l = mid + 1;
			}
		}
		cout << ans << '\n';
	}
}

int main() {
	// ios::sync_with_stdio(false);
	// cin.tie(nullptr);

	int T; cin >> T;
	while(T --) {
		solve();
	}
	return 0;
}

D - Shuffle

题意：
给定一个字符串\(s\)和一个整数\(k\)，你可以对任意一个包含恰好\(k\)个\(1\)连续的子序列的做\(shuffle\)操作，即重排这个序列中的所有字母，问最后能获得字符串共有多少种？

法Ⅰ直接考虑答案，法Ⅱ是从部分扩展到整体。

法 Ⅰ

• 计数类问题，很明显我们如果直接统计每个有\(k\)个\(1\)的子串，必然会有很多重复的情况，我们要做的就是去掉这些重复的情况
• 在长度为\(n\)的子串中包含\(k\)个1，那他们的打乱方案就是\(C_n^k\)
• 如下图所示
  
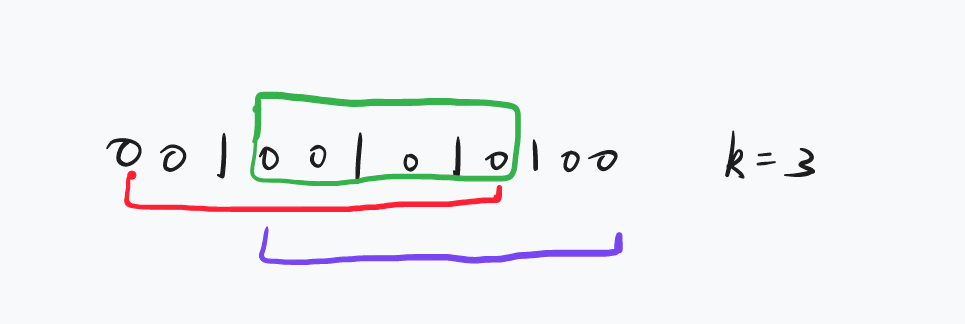
• 红色序列和蓝色序列均符合要求，但是明显他们中间夹着的绿色的部分会在重复计算，按照容斥原理我们在加上红蓝部分的同时减去绿色部分即可
• 预先处理一下所有\(1\)的位置，即可\(O(n)\)完成

#include <bits/stdc++.h>

using namespace std;

//法Ⅰ 容斥计数
const int mod = 998244353;

int C[5010][5010];

int main() {
	for(int i = 0;i <= 5000;i ++) {
		C[i][0] = 1;
		for(int j = 1;j <= i;j ++) {
			C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;		
		}
	}//预处理组合数
	int n,k; cin >> n >> k;
	string s; cin >> s;
	vector<int>p;
	p.push_back(0);//两端假装放进1 来简化边界计算
	for(int i = 0;i < n;i ++) {
		if(s[i] == '1') {
			p.push_back(i + 1);
		}
	}
	p.push_back(n + 1);
	long long ans = 0;
	for(int i = k;i <= p.size() - 2;i ++) {
		int len = p[i + 1] - 1 - (p[i - k] + 1) + 1;
		ans = (ans + C[len][k]) % mod;
		if(i > k) {
			len = p[i] - 1 - (p[i - k] + 1) + 1;
			ans = ((ans - C[len][k - 1]) % mod + mod) % mod;
		}
	}
	if(k == 0 || p.size() - 2 < k) {
		cout << "1\n";
	} else {
		cout << ans << '\n';
	}
	return 0;
}

法 Ⅱ

• 题目所给数据范围\(n \le 5000\)，那么一定会存在\(O(n^2)\)做法
• 恰好等于\(k\)个\(1\)的打乱方法等于其字串小于等于\(k\)个\(1\)的打乱方法的总和，考虑扩展时重复的情况去掉即可
• 从子串\([l,r]\)向\([l-1,r+1]\)扩展时，考虑什么情况下会重复，即保持\(l-1\)和\(r+1\)的原样会重复，因为打乱内层时这两个位置不受影响。所以当打乱到这层时，我们必须这两个位置和上次的位置保持不一致才是和内层操作时不一样的方案数贡献
• 分类讨论一下即可，是0强行放1，1强行放0

#include <bits/stdc++.h>

using namespace std;

const int mod = 998244353;

int C[5010][5010],pre[5010];

int main() {
	for(int i = 0;i <= 5000;i ++) {
		C[i][0] = 1;
		for(int j = 1;j <= i;j ++) {
			C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;		
		}
	}
	int n,k; cin >> n >> k;
	string s; cin >> s;
	s = ' ' + s;
	for(int i = 1;i <= n;i ++) {
		pre[i] = pre[i - 1] + (s[i] == '1');
	}
	if(k == 0 || pre[n] < k) {
		cout << "1\n";
		return 0;
	}
	long long ans = 1;//自己本身是一种
	for(int i = 1;i <= n;i ++) {
		for(int j = i + 1;j <= n;j ++) {
			if(pre[j] - pre[i - 1] > k) continue;
			int cnt1 = pre[j] - pre[i - 1];
			int cnt0 = j - i + 1 - cnt1;
			if(s[i] == '0') {
				cnt1 --;
			} else {
				cnt0 --;
			}
			if(s[j] == '0') {
				cnt1 --;
			} else {
				cnt0 --;
			}
			if(cnt1 < 0 || cnt0 < 0) continue;
			ans = (ans + C[cnt0 + cnt1][cnt1]) % mod;
		}
	}
	cout << ans << '\n';
	return 0;
}