大厂面试高频题目-回溯

第77题. 组合

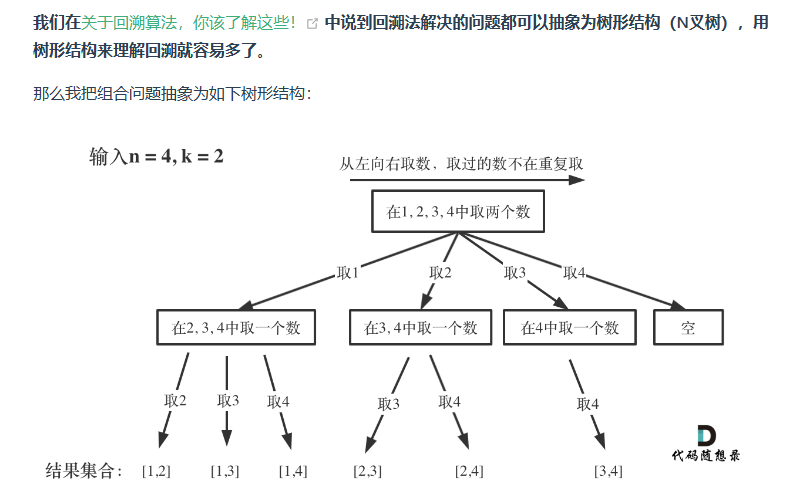
给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

思考

回溯的模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

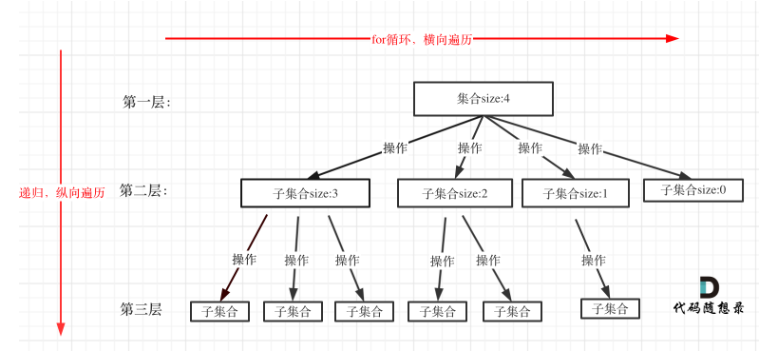
每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

图中可以发现n相当于树的宽度，k相当于树的深度。

1. 组合问题需要start_index来避免重复结果。
2. 可以剪枝

class Solution:
    def __init__(self):
        self.res_list = []
        self.res_list_all = []
    def backtracking(self,n,k,start_index):
        if k == len(self.res_list):
            self.res_list_all.append(self.res_list[:])
            return
        else:
            for i in range(start_index,n+1):
                if len(self.res_list)+ 1 + n - i < k:
                     break
                self.res_list.append(i)
                #print(self.res_list)
                self.backtracking(n,k,i+1)
                self.res_list.pop()
    def combine(self, n: int, k: int) -> List[List[int]]:
        self.backtracking(n,k,1)
        return self.res_list_all

216.组合总和III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。
解集不能包含重复的组合。
示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

思考

这道题主要是要剪枝，

1. 总和大于target时，提前返回。
2. 元素个数>k时,break

class Solution:
    def __init__(self):
        self.path = []
        self.res_list_all = []
        self.sum = 0
    def backtracking(self,candidates,target,k,start_index):
        # 剪枝1
        if self.sum > target:
            return 
        if len(self.path) == k:
            if self.sum == target:
                self.res_list_all.append(self.path[:])
            return 
        else:
            for i in range(start_index,len(candidates)):
                # 剪枝2
                if len(self.path)>=k:
                    break
                self.path.append(candidates[i])
                self.sum+=candidates[i] 
                self.backtracking(candidates,target,k,i+1)
                self.path.pop()
                self.sum-=candidates[i]
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        candidates = [1,2,3,4,5,6,7,8,9]
        self.backtracking(candidates,n,k,0)
        return self.res_list_all

7.电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:
输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

class Solution:
    def __init__(self):
        self.letterMap = [
            "",     # 0
            "",     # 1
            "abc",  # 2
            "def",  # 3
            "ghi",  # 4
            "jkl",  # 5
            "mno",  # 6
            "pqrs", # 7
            "tuv",  # 8
            "wxyz"  # 9
        ]
        self.result = []
        self.s = []
    def backtracking(self,digits,index):
        if len(digits) == len(self.s):
            self.result.append(''.join(self.s))
            return
        for c in self.letterMap[int(digits[index])]:
            self.s.append(c)
            self.backtracking(digits,index+1)
            self.s.pop()
    def letterCombinations(self, digits: str) -> List[str]:
        if len(digits) == 0:
            return self.result
        self.backtracking(digits,0)
        return self.result

39. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。

思考

这道题的特点是可以重复选取。
因此for循环内遍历的时候，start_index = i

class Solution:
    def __init__(self):
        self.path = []
        self.res_list_all = []
        self.sum = 0
    def backtracking(self,candidates,target,start_index):
        if self.sum == target:
            self.res_list_all.append(self.path[:])
            return 
        elif self.sum > target:
            return 
        else:
            for i in range(start_index,len(candidates)):
                self.path.append(candidates[i])
                self.sum+=candidates[i]
                self.backtracking(candidates,target,i)
                self.path.pop()
                self.sum-=candidates[i]
                
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        self.backtracking(candidates,target,0)
        return self.res_list_all

排序后，回溯的过程可以剪枝，同一层，前面的数和已经超了的话，后面的就不用再试了，因为后面的数更大。

class Solution:
    def __init__(self):
        self.path = []
        self.res_list_all = []
        self.sum = 0
    def backtracking(self,candidates,target,start_index):
        if self.sum == target:
            self.res_list_all.append(self.path[:])
            return 
        elif self.sum > target:
            return 
        else:
            for i in range(start_index,len(candidates)):
                if self.sum+candidates[i] > target:
                    break
                self.path.append(candidates[i])
                self.sum+=candidates[i]
                self.backtracking(candidates,target,i)
                self.path.pop()
                self.sum-=candidates[i]
                
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        self.backtracking(candidates,target,0)
        return self.res_list_all

40. 组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

思考

这道题的难点是要在回溯中去重，即去除重复的组合。
两种方法:

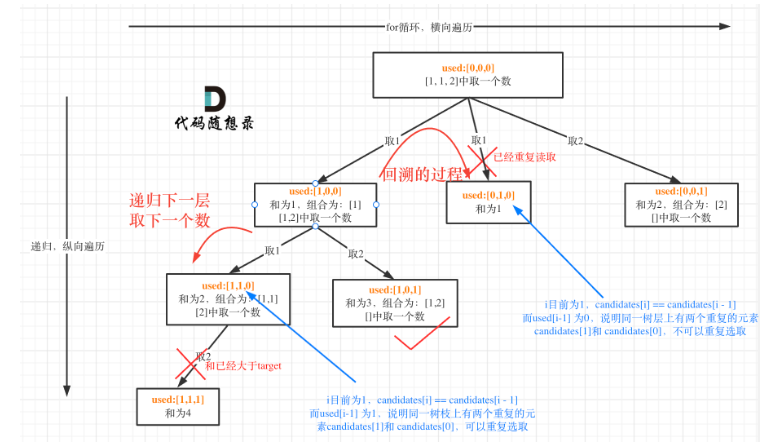
1. 需要定义一个used数组。
   used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
   used[i - 1] == false，说明同一树层candidates[i - 1]使用过
   
   2. 判断条件增加i>start_index
   两种方案都需要先排序才能去重。

方案二的方法

class Solution:
    def __init__(self):
        self.res = []
        self.res_all = []
        self.sum = 0
    def backtracking(self,candidates,target,start_index):
        if self.sum > target:
            return
        if self.sum == target:
            self.res_all.append(self.res[:])
            return
        for i in range(start_index,len(candidates)):
            if i > start_index and (candidates[i-1] == candidates[i]):
                continue
            self.sum+=candidates[i]
            self.res.append(candidates[i])
            self.backtracking(candidates,target,i+1)
            self.res.pop()
            self.sum-=candidates[i]
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        self.backtracking(candidates,target,0)
        return self.res_all

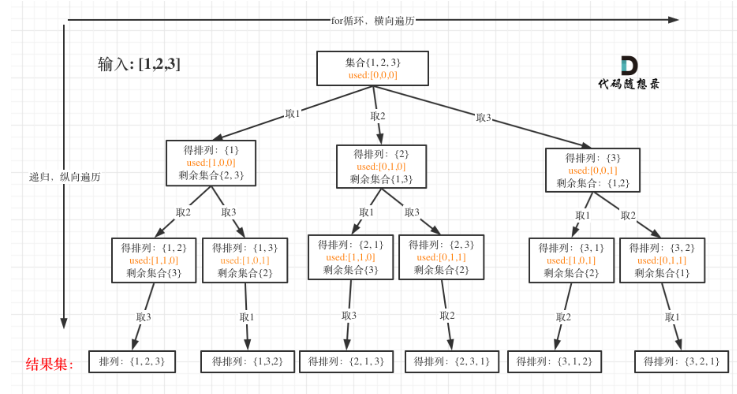
46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：

输入：nums = [1]
输出：[[1]]

思考

1. 排列问题不需要start_index
2. 需要一个used数字，来判断哪些元素已经取过了。因为元素不能重复取。

class Solution:
    def __init__(self):
        self.res_all = []
        self.res = []
    def backtracking(self,nums,used):
        if len(self.res) == len(nums):
            self.res_all.append(self.res[:])
            return
        for i in range(len(nums)):
            if used[i]:
                continue
            used[i] = True
            self.res.append(nums[i])
            self.backtracking(nums,used)
            self.res.pop()
            used[i] = False
        
    def permute(self, nums: List[int]) -> List[List[int]]:
        used = [False]*len(nums)
        self.backtracking(nums,used)
        return self.res_all

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的
子集
（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

思考

本题元素不重复，不需要考虑去重，标准的求子集的模板题。收集所有节点。

class Solution:
    def __init__(self):
        self.path = []
        self.res = []
    def backtracking(self,nums,start_index):
        self.res.append(self.path[:])
        if len(self.path) == len(nums):
            return
        for i in range(start_index,len(nums)):
            self.path.append(nums[i])
            self.backtracking(nums,i+1)
            self.path.pop()
    def subsets(self, nums: List[int]) -> List[List[int]]:
        self.backtracking(nums,0)
        return self.res

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]
示例 2：

输入：n = 1
输出：["()"]

思考

有点绕的一道题，暴力回溯+判断括号匹配肯定可以实现，时间复杂度太高。需要在回溯中进行有效性的判断或者直接生成有效的括号。
有效加入的思路：
左括号个数为left，右括号个数为right
1、left只要不超过n，可以一直加，比如((((((((
2、right只有在小于left的时候，才能加入，否则肯定无效了。比如（）（）时不能在加入右括号。

小技巧：代码实现时，可以把回溯写成函数内的函数，就不用再用init初始化全局变量了。

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        left = 0
        right = 0
        path = []
        res = []
        def backtracking(left,right,n):
            if len(path) == 2*n:
                res.append(''.join(path))
                return
            if left<n:
                path.append('(')
                backtracking(left+1,right,n)
                path.pop()
            if left>right:
                path.append(')')
                backtracking(left,right+1,n)
                path.pop()
        backtracking(0,0,n)
        return res

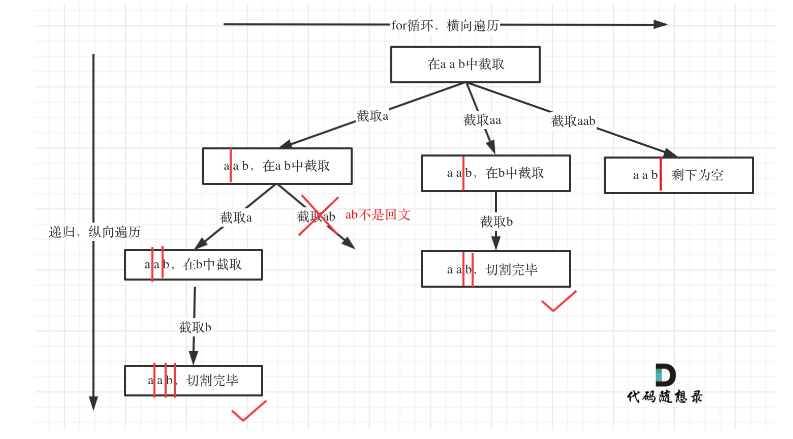
131.分割回文串

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]

思考

分割问题本质上也是求组合问题。start_index表示分割线。

def is_huiwen(s):
    i = 0
    j = len(s)-1
    while i<j:
        if s[i]==s[j]:
            i+=1
            j-=1
        else:
            return False
    return True
class Solution:
    def partition(self, s: str) -> List[List[str]]:
        def backtracking(s,star_index):
            if star_index == len(s):
                res.append(path[:])
                return
            for i in range(star_index,len(s)):
                if is_huiwen(s[star_index:i+1]):
                    path.append(s[star_index:i+1])
                    backtracking(s,i+1)
                    path.pop()
        path = []
        res = []
        backtracking(s,0)
        return res