Treap

BST 可以看我去年九月份写的博客。

定义

Treap 是 Tree 与 Heap 的结合，顾名思义，它既满足 BST 的性质，同时也满足大根堆的性质。

Treap 的各个基本操作时间复杂度均为 \(O(\log n)\) 级别，这是因为一棵随机的树的期望高度为 \(O(\log n)\) 级别的，而 Treap 通过其堆性质保证了树结构的随机性。

Treap 事实上是一种笛卡尔树，而后者有性质：当所有的点的优先级都已知时，树的结构唯一。

这篇博客中的码风与我现在的码风很不一样，这是因为这个模板是我在去年十二月份时写的。而且现在也不会再用 Treap 来实现平衡树了，FHQ 显然是更好的选择。

实现

首先看看 Treap 中到底要维护些什么东西：

int val[N], prm[N], ch[N][2], size[N]; 
int cnt, root;

其中，val 是节点的权值，prm 是节点的优先级（用于保持堆性质），ch 为节点的左右子节点，size 为每个节点子树的大小（包括自身），而 cnt 是节点代表数字的个数。

旋转

为了维持 Treap 的平衡，需要引入旋转的概念，这也是一个在其他平衡树中相当常见的概念。

如下图，旋转分为左旋和右旋：

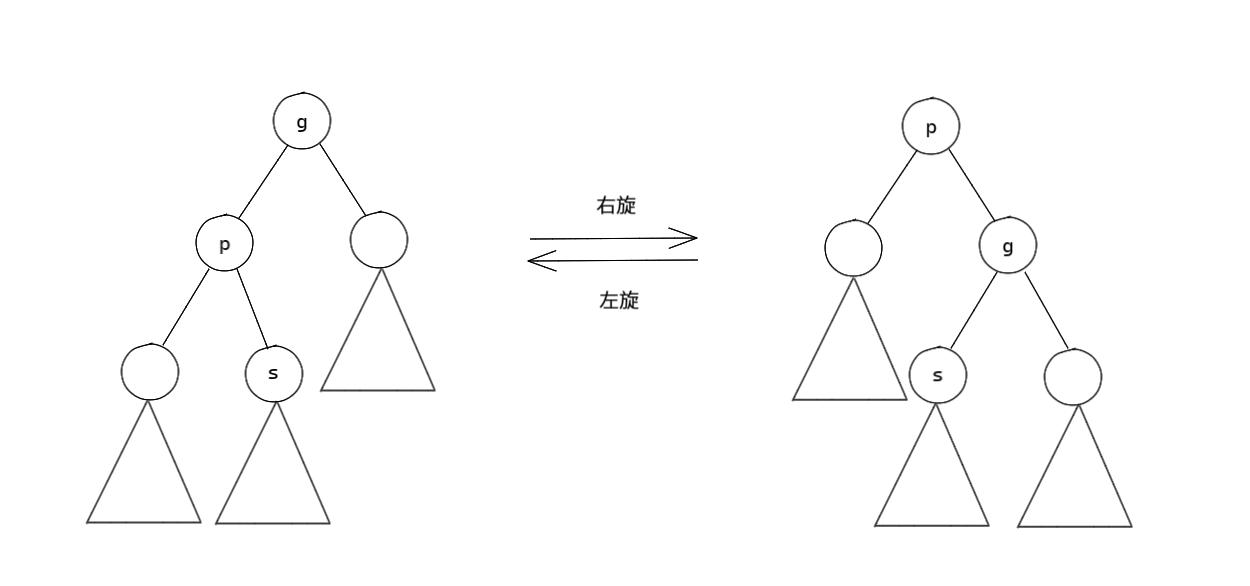
容易发现，在旋转前后，Treap 的 BST 性质是不会被破坏的，这可以由其的中序遍历看出。

旋转的主要作用是用于维护 Treap 的堆性质。可以看出旋转的过程会交换上下两节点的父子关系，类似于堆中的向上浮动。也就是说，左旋一个节点可使左儿子成为当前节点的父亲，右旋一个节点可使右儿子成为当前节点的父亲。

根据这个图，代码就很容易写出来了，可以用两个函数来表示左旋和右旋，当然也可以只用一个。

void rotate(int &u, int d) { 
  int k = ch[u][d]; 
  ch[u][d] = ch[k][d ^ 1]; 
  ch[k][d ^ 1] = u; 
  size[k] = size[u]; 
  update(u), u = k; 
  return;
}

其中，d == 0 表示左旋，d == 1 表示右旋。

Treap 的几个主要操作都是递归的，因此我们需要分情况讨论。为了便利，我们统一记当前节点为 \(u\)。

其实 Treap 的几个操作与普通的 BST 很相似，重点在于利用旋转来维护平衡的部分。

插入

设待插入的值为 \(x\)。

• 当当前节点为空，即 \(u = 0\) 时，新建一个节点来存储当前数字；
• 否则，若 \(val_u \le x\)，则递归地在右子树中插入。若 \(val_u \gt x\)，则递归地在左子树中插入。

是不是跟普通 BST 一模一样？重点在于插入之后的部分：维护平衡。

• 若左子树存在且其优先级大于 \(u\) 的优先级，则左旋 \(u\)；
• 若右子树存在且其优先级大于 \(u\) 的优先级，则右旋 \(u\)。

这也就是为了维护 Treap 的堆性质。最后，不要忘了更新子树大小。

void insert(int &u, int x) { 
  if (!u) return (void)(init(x), u = cnt); 
  size[u]++; 
  if (x >= val[u]) insert(ch[u][1], x); 
  else insert(ch[u][0], x); 
  if (ch[u][0] && prm[u] > prm[ch[u][0]]) rotate(u, 0); 
  if (ch[u][1] && prm[u] > prm[ch[u][1]]) rotate(u, 1); 
  update(u); 
  return; 
}

删除

删除较为复杂，需要讨论的情况更多了。仍然设待删除的值为 \(x\)。

• 当 \(val_u = x\) 时：
  • 如果当前节点为叶子结点，直接删去 \(u\) 即可；
  • 如果当前节点只有一个儿子，则用这个儿子代替 \(u\) 即可；
  • 否则，用优先级较大的儿子代替 \(u\)，并递归地删除 \(u\) 所代表的节点，直到其满足上述的两个条件之一。
• 否则，若 \(val_u < x\)，则在右子树中递归地删除 \(x\)，若 \(val_u >x\)，则在左子树中递归地删除 \(x\)。

void del(int &u, int x) {
  size[u]--;
  if (val[u] == x) {
    if (!ch[u][0] && !ch[u][1]) 
        return (void)(u = 0);
    if (!ch[u][0] || !ch[u][1]) 
        return (void)(u = ch[u][0] + ch[u][1]);
    if (prm[ch[u][0]] < prm[ch[u][1]]) 
        return (void)(rotate(u, 0), del(ch[u][1], x));
    else (void)(rotate(u, 1), del(ch[u][0], x));
  } else {
    if (val[u] >= x) del(ch[u][0], x);
    else del(ch[u][1], x);
    update(u);
    return;
  }
}

以上是两个会改变树的形态的操作，因此节点 \(u\) 需要传引用。而下面四个操作，由于不会改变树的形态，则与普通 BST 无异。

求排名

一个数的排名 \(rank\) 定义为比它小的数的个数加一。

BST 有性质：一个节点左子树中的所有数都比当前节点的树要小，其右子树中的所有数都比当前节点的数要大。于是我们可以通过子树的大小来判断当前数的排名。

int getRankByNum(int u, int x) {
  if (!u) return 0;
  if (x > val[u]) return size[ch[u][0]] + getRankByNum(ch[u][1], x) + 1;
  return getRankByNum(ch[u][0], x);
}

求指定排名的数

与求排名相似，同样是利用子树的大小来判断待求数是位于左子树中还是右子树中。

int getNumByRank(int u, int x) {
  if (x == size[ch[u][0]] + 1) 
    return val[u];
  if (x > size[ch[u][0]] + 1) 
    return getNumByRank(ch[u][1], x - size[ch[u][0]] - 1);
  return getNumByRank(ch[u][0], x);
}

求前驱后继

一个数的前驱指的是严格小于它的最大数，而后继指的是严格大于它的最小数。这两个比较相似，放在一块说了。

以前驱为例。对于某一特定节点，由 BST 的性质可知其前驱为其左子树中的最大值。于是可以设计如下流程：

• 当 \(val_u \ge x\) 时，递归地在左子树中查找；
• 此时若 \(u = 0\)，返回 0，否则，尝试在右子树中查找前驱；若右子树中不存在比 \(x\) 小的数，返回当前节点的值，否则，返回在右子树中查找到的值。

后继也有类似类似的性质，即一个特定的数的后继为其右子树中的最小值。

int getPrecursor(int u, int x) {
  if (!u) return 0;
  if (val[u] >= x) return getPrecursor(ch[u][0], x);
  int tmp = getPrecursor(ch[u][1], x);
  return (tmp ? tmp : val[u]);
}

int getSuccessor(int u, int x) {
  if (!u) return 0;
  if (val[u] <= x) return getSuccessor(ch[u][1], x);
  int tmp = getSuccessor(ch[u][0], x);
  return (tmp ? tmp : val[u]);
}

模板

就挂个模板吧，反正也不会用。

struct Treap {
  int val[N], prm[N], ch[N][2], size[N];
  int cnt, root;

  Treap() { root = 0; };

  void init(int u) {
    val[++cnt] = u, prm[cnt] = rand();
    ch[cnt][0] = ch[cnt][1] = 0, size[cnt] = 1;
    return;
  }

  void update(int u) {
    size[u] = size[ch[u][0]] + size[ch[u][1]] + 1;
    return;
  }

  void rotate(int &u, int d) {
    int k = ch[u][d];
    ch[u][d] = ch[k][d ^ 1];
    ch[k][d ^ 1] = u;
    size[k] = size[u];
    update(u), u = k;
    return;
  }

  void insert(int &u, int x) {
    if (!u) return (void)(init(x), u = cnt);
    size[u]++;
    if (x >= val[u]) insert(ch[u][1], x);
    else insert(ch[u][0], x);
    if (ch[u][0] && prm[u] > prm[ch[u][0]]) rotate(u, 0);
    if (ch[u][1] && prm[u] > prm[ch[u][1]]) rotate(u, 1);
    update(u);
    return;
  }

  void del(int &u, int x) {
    size[u]--;
    if (val[u] == x) {
      if (!ch[u][0] && !ch[u][1]) 
        return (void)(u = 0);
      if (!ch[u][0] || !ch[u][1]) 
        return (void)(u = ch[u][0] + ch[u][1]);
      if (prm[ch[u][0]] < prm[ch[u][1]]) 
        return (void)(rotate(u, 0), del(ch[u][1], x));
      else (void)(rotate(u, 1), del(ch[u][0], x));
    } else {
      if (val[u] >= x) del(ch[u][0], x);
      else del(ch[u][1], x);
      update(u);
      return;
    }
  }

  int getRankByNum(int u, int x) {
    if (!u) return 0;
    if (x > val[u]) return size[ch[u][0]] + getRankByNum(ch[u][1], x) + 1;
    return getRankByNum(ch[u][0], x);
  }

  int getNumByRank(int u, int x) {
    if (x == size[ch[u][0]] + 1) 
      return val[u];
    if (x > size[ch[u][0]] + 1) 
      return getNumByRank(ch[u][1], x - size[ch[u][0]] - 1);
    return getNumByRank(ch[u][0], x);
  }

  int getPrecursor(int u, int x) {
    if (!u) return 0;
    if (val[u] >= x) return getPrecursor(ch[u][0], x);
    int tmp = getPrecursor(ch[u][1], x);
    return (tmp ? tmp : val[u]);
  }

  int getSuccessor(int u, int x) {
    if (!u) return 0;
    if (val[u] <= x) return getSuccessor(ch[u][1], x);
    int tmp = getSuccessor(ch[u][0], x);
    return (tmp ? tmp : val[u]);
  }
};