DLX
DLX
概述
DLX(Dancing Links X,舞蹈链),是由伟大的计算机科学家 Knuth 发明的一种数据结构,其主要用于解决精确覆盖问题与重复覆盖问题。
我是在解决数独问题时了解到这种奇妙的数据结构的,它是目前解决数独问题最为高效的方法之一。当然,它的功能远不止于此,许多对摆放位置有约束的、正解为 DFS 的题目,都能用其解决,包括 8 皇后问题等。
互联网上上已经有许多关于 DLX 的优秀博客了,我只写一些我自己的理解。
这篇文章,主要参考了 OI Wiki 与其上的模板代码。
流程
X 算法
要学习 DLX,首先要了解它的基础:X 算法。
我们用互联网上较为常见的一个矩阵举例:
现在我们考虑从这个矩阵中选出若干行,使得矩阵的每一列都恰好包含一个 \(1\)。
一种显然的做法是暴力地枚举每一行选或者不选,这样在一个 \(n\) 行 \(m\) 列的矩阵中,复杂度是 \(O(2^nnm)\),这样是满足不了我们的需求的。
于是我们有了一种优化过后的方法,也就是 X 算法。
枚举矩阵中的每一行,我们将这一行用红色标记出来,表示选择了这一行后,将其删去:
再把这一行中,包含 \(1\) 的列用红色标记出来,表示删除了这一列,因为此时这一列已经包含了 1,我们不再需要它了:
我们每选择一行,这一行里包含 \(1\) 的列就不能有更多的 \(1\) 了,于是我们将选择的列中值为 \(1\) 的行删去:
删去它们!
这时我们得到了一个更小的 \(01\) 矩阵。再在这个矩阵上重复上述操作:
选取第一行:
标记含 1 的列:
再标记选取的列值为 1 的行:
删除:
发现矩阵空了。那么此时我们是不是就找到了一组解呢?当然不是,由于上次选择的行其值为 \(1 \, 0 \, 1 \, 1\),有一个 \(0\),也就意味着还有一列没有选,但是删去这行后,矩阵为空,不能再选更多的行了,那么这种选法就并非为一组解。
回溯到上一步,这次我们选第二行:
继续上述过程,可以得到:
得到:
显然,直接删掉第一行,就可以得到一组解。
那么也就是说,我们选择原矩阵中的第一、四、五行,就可以得到一组解。
双向循环十字链表
不难看出,暴力地模拟以上操作,复杂度仍然是指数级的。因此,我们需要一种合适的数据结构来实现以上算法。
发现 X 算法的过程中有大量的删除、恢复行、列的操作,于是 Knuth 在他的论文中提出了双向循环十字链表这种数据结构,用于高效地实现 X 算法。
对于链表中的每一个节点,我们维护以下几个值:右节点 \(R\),左节点 \(L\),上节点 \(U\),下节点 \(D\),节点所在的行 \(row\),节点所在的列 \(col\)。
对于链表中的每一行,维护一个头指针 \(first\);对于每一列,维护每一列中的节点个数 \(siz\)。
画成图,大概就是这样的:
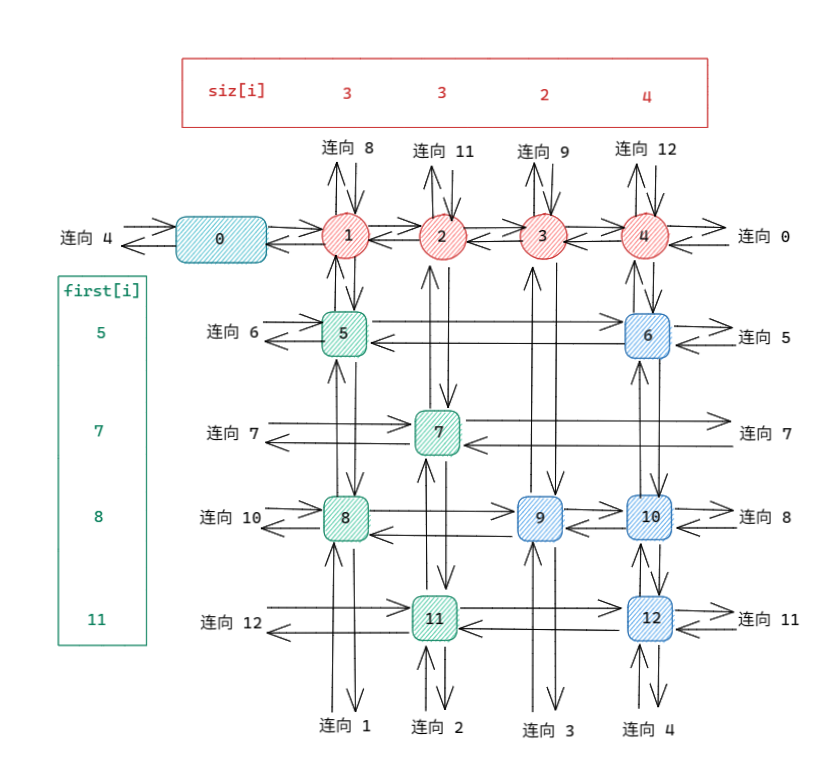
接下来我们来说说几个必要的操作。
初始化
初始化操作 build(int r, int c),表示初始化一个 \(r\) 行 \(c\) 列的双向循环十字链表。
初始化时,我们在每一列都新建一个节点,作为这一列的头结点。具体地,用节点编号为 \(i\) 的节点作为第 \(i\) 列的头结点,这样在插入新节点时会方便很多。
特别地,我们钦定 \(0\) 号节点为整个链表的指示节点,用于表示整个链表的状态。
为了体现数据结构名称中的“循环”二字,我们令 \(0\) 号节点的左节点为 \(c\),\(c\) 节点的右节点为 \(0\);由于此时链表为空,每个节点的上节点与下节点都为其本身。
void build(int r, int c) {
for (int i = 0; i <= c; i++) {
L[i] = i - 1, R[i] = i + 1;
U[i] = D[i] = i;
}
L[0] = c, R[c] = 0;
cnt = c;
return;
}
插入
插入操作 insert(int r, int c),表示在第 \(r\) 行第 \(c\) 列插入一个 \(1\)。
插入操作要分为两种情况讨论:
- 当前行为空,那么可以直接插入,再把 \(first_r\) 指向这个节点,\(c\) 节点的正下方;
- 当前行不为空,那么我们选择把这个节点插入至 \(first_r\) 的正右边,\(c\) 节点的正下方。
维护上下节点的操作都是一样的,这没什么好说的。维护左右节点的方法跟普通的双向循环链表差不多。
void insert(int r, int c) {
col[++cnt] = c, row[cnt] = r;
siz[c]++;
D[cnt] = D[c], U[D[c]] = cnt;
U[cnt] = c, D[c] = cnt;
if (!first[r]) {
first[r] = L[cnt] = R[cnt] = cnt;
} else {
R[cnt] = R[first[r]], L[R[first[r]]] = cnt;
L[cnt] = first[r], R[first[r]] = cnt;
}
return;
}
删除
双向循环十字链表的删除操作 remove(c),表示删除第 \(c\) 列的节点以及与其相关的行。
首先断开第 \(c\) 列与其他列的连接,这个简单,像普通的双向链表一样维护就行了:R[L[c]] = R[c], L[R[c]] = L[c]。
然后我们考虑删去与其有关的行,那么我们顺着这一列向下走,删掉经过的每一行就好了:U[D[j]] = U[j], D[U[j]] = D[j]。
还要维护这一列的节点个数:siz[col[j]]--。
void remove(int c) {
L[R[c]] = L[c], R[L[c]] = R[c];
for (int i = D[c]; i != c; i = D[i]) {
for (int j = R[i]; j != i; j = R[j]) {
U[D[j]] = U[j], D[U[j]] = D[j];
siz[col[j]]--;
}
}
return;
}
恢复
恢复操作 recover(c),表示恢复第 \(c\) 列以及与其有关的行。
有了删除操作之后,我们只需要倒着做一遍就行了,但是一定要记得:操作顺序要严格相反。
先恢复有关的行:U[D[j]] = D[U[j]] = j;
维护列的大小:siz[col[j]]++。
再把第 \(c\) 列连回去:R[L[c]] = L[R[c]] = c。
void recover(int c) {
for (int i = U[c]; i != c; i = U[i]) {
for (int j = L[i]; j != i; j = L[j]) {
U[D[j]] = D[U[j]] = j;
siz[col[j]]++;
}
}
L[R[c]] = R[L[c]] = c;
return;
}
Dance!
最后,当然就是在链表上跳舞了!
dance(int dep) 函数用于求解具体问题,具体过程与上边 X 算法的过程差不多,它是递归的,dep 参数表示的是当前的搜索深度。
首先,要确定结束状态。还记得那个 \(0\) 号节点吗?它作为整个链表状态的指示器,其主要作用就是判断链表是否为空。与 \(0\) 号节点相连的是链表的所有列的头结点,那么,当 \(0\) 号节点的左右节点为其本身时,链表中的每一列也就被删空了,此时,我们就抵达了结束状态。
当链表不为空时,我们要在矩阵中随便选一列,删掉它,然后进行下一步操作。但这样做显然是盲目的,有没有更好的办法呢?是有的,我们可以每次都选择元素个数最小的一列删除,这样可以减少搜索树的大小。记被删除的列是 \(c\),那么需要调用一次 remove(c)。
删掉这列本身后,还要删掉与这一列相关的行。由于我们需要把所有可能可行的状态都搜到,所以要枚举该列上的每一行,尝试删除与这一行相关的列。每删除一行,就要递归地调用一次 dance(dep + 1),而且要记得回溯。
上述操作与上边所写的 X 算法操作的主要区别就是:X 算法首先枚举行,而上述操作首先枚举的是列。很显然,这只是顺序问题,本质上是等价的。
最后,要恢复删去的这一列,也就是调用 recover(c)。
显然我们所需要的答案,也就是删除的矩阵的行,是隐藏在递归的过程中了。因此,我们可以开一个栈数组 \(stk\) 来记录答案。
bool dance(int dep) {
if (!R[0]) {
// 对答案的处理
return true;
}
int c = R[0];
for (int i = R[0]; i != 0; i = R[i]) {
if (siz[i] < siz[c]) {
c = i;
}
}
remove(c);
for (int i = D[c]; i != c; i = D[i]) {
stk[dep] = row[i];
for (int j = R[i]; j != i; j = R[j]) {
remove(col[j]);
}
if (dance(dep + 1)) {
return true;
}
for (int j = L[i]; j != i; j = L[j]) {
recover(col[j]);
}
}
recover(c);
return false;
}
上边这份模板代码显然只能搜出一组解,如果你要求出问题的所有解的话,可以这么写:
void dance(int dep) {
if (!R[0]) {
// 对一组答案的处理
return;
}
int c = R[0];
for (int i = R[0]; i != 0; i = R[i]) {
if (siz[i] < siz[c]) {
c = i;
}
}
remove(c);
for (int i = D[c]; i != c; i = D[i]) {
stk[dep] = row[i];
for (int j = R[i]; j != i; j = R[j]) {
remove(col[j]);
}
dance(dep + 1);
for (int j = L[i]; j != i; j = L[j]) {
recover(col[j]);
}
}
recover(c);
return;
}
模板
模板是很好写的,至少比平衡树好。能用 DLX 解决的问题基本上都可以套用一份模板代码,给一份给大家参考一下。
struct DLX {
static const int MAX = 1e5 + 50;
int n, m, cnt;
std::vector<int> L, R, U, D;
std::vector<int> col, row;
std::vector<int> siz, first, stk;
DLX(int n, int m) {
this->n = n;
this->m = n;
L.resize(MAX), R.resize(MAX), U.resize(MAX), D.resize(MAX);
col.resize(MAX), row.resize(MAX), siz.resize(MAX, 0), first.resize(MAX, 0);
stk.resize(MAX);
build(n, m);
return;
}
void build(int r, int c) {
for (int i = 0; i <= c; i++) {
L[i] = i - 1, R[i] = i + 1;
U[i] = D[i] = i;
}
L[0] = c, R[c] = 0;
cnt = c;
return;
}
void insert(int r, int c) {
col[++cnt] = c, row[cnt] = r;
siz[c]++;
D[cnt] = D[c], U[D[c]] = cnt;
U[cnt] = c, D[c] = cnt;
if (!first[r]) {
first[r] = L[cnt] = R[cnt] = cnt;
} else {
R[cnt] = R[first[r]], L[R[first[r]]] = cnt;
L[cnt] = first[r], R[first[r]] = cnt;
}
return;
}
void remove(int c) {
L[R[c]] = L[c], R[L[c]] = R[c];
for (int i = D[c]; i != c; i = D[i]) {
for (int j = R[i]; j != i; j = R[j]) {
U[D[j]] = U[j], D[U[j]] = D[j];
siz[col[j]]--;
}
}
return;
}
void recover(int c) {
for (int i = U[c]; i != c; i = U[i]) {
for (int j = L[i]; j != i; j = L[j]) {
U[D[j]] = D[U[j]] = j;
siz[col[j]]++;
}
}
L[R[c]] = R[L[c]] = c;
return;
}
bool dance(int dep) {
if (!R[0]) {
// 处理答案
return true;
}
int c = R[0];
for (int i = R[0]; i != 0; i = R[i]) {
if (siz[i] < siz[c]) {
c = i;
}
}
remove(c);
for (int i = D[c]; i != c; i = D[i]) {
stk[dep] = row[i];
for (int j = R[i]; j != i; j = R[j]) {
remove(col[j]);
}
if (dance(dep + 1)) {
return true;
}
for (int j = L[i]; j != i; j = L[j]) {
recover(col[j]);
}
}
recover(c);
return false;
}
};
时间复杂度?
DLX 的时间复杂度为 \(O(c ^ n)\),看似是指数级的,但是其底数为一个非常接近 \(1\) 的常数,指数 \(n\) 则是矩阵中 \(1\) 的个数。
例题
DLX 问题重在建模,例题以后会补的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号