2 月 26 日测试题解
2 月 26 日测试题解
感冒了,一个正解也没想出来。但是混了大量的部分分,因此我会对各个部分分做出解释。
最近在学习 \(\texttt{j}\textcolor{red}{\texttt{iangly}}\) 的码风,所以有的代码可能写的有些奇怪。
T1
题意
给你两个序列 \(a\) 和 \(b\),长度分别为 \(n\) 与 \(m\),你可以在 \(a\) 中取任意个数,再在 \(b\) 中取任意个数,但是不能不取。现在问你使从 \(a\) 中取出来的数之和与 \(b\) 中的相等的最小取数次数是多少,不存在则输出 \(-1\)。
\(n, m \le 100\)。
思路
考场上写的是二进制枚举,混了 \(\text{50pts}\),然而正解是一个显而易见的背包。
那我就把两个都说一下吧。
\(\text{50pts}\)
考虑二进制枚举,分别预处理出 \(a\) 和 \(b\) 中的所有可能出现的值以及其最小取数次数存到一个数组里,然后扫一遍,若这个数字在 \(a\) 和 \(b\) 中都可以出现,则尝试用其取数次数之和更新答案。
时间复杂度 \(O(2^n + 2^m)\),但是事实上很好写,基本挂不了。
\(\text{100pts}\)
有了 \(\text{50pts}\) 的做法之后,其实思路是不难想的。
首先可以肯定大体思路没有错,就是预处理出可能出现的数的最小取数个数。对于上边做法中复杂度最高的地方,即二进制枚举的部分,我们可以把其看成一个精确 \(01\) 背包问题。例如 \(a\),背包的容量是 \(\sum a_i\),而物品就是每一个 \(a_i\)。\(b\) 同理。
代码
\(\text{50pts}\)
#include <iostream>
#include <cstring>
using namespace std;
using i64 = long long;
static const int N = 150, M = 1e6 + 50, INF = 0x3f3f3f3f;
int n, m;
int a[N], b[N];
bool bucket[M][2];
int cnt[M][2], ans = INF;
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
memset(cnt, 0x3f, sizeof(cnt));
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
bucket[a[i]][0] = true;
cnt[a[i]][0] = 1;
}
cin >> m;
for (int i = 1; i <= m; i++) {
cin >> b[i];
bucket[b[i]][1] = true;
cnt[b[i]][1] = 1;
}
for (int i = 1; i < (1 << n); i++) {
int tmp = i, sum = 0, cur = 0;
for (int j = 0; (1 << j) <= tmp; j++) {
if (tmp & (1 << j)) {
sum += a[j + 1];
cur++;
}
}
bucket[sum][0] = true;
cnt[sum][0] = min(cur, cnt[sum][0]);
}
for (int i = 1; i < (1 << m); i++) {
int tmp = i, sum = 0, cur = 0;
for (int j = 0; (1 << j) <= tmp; j++) {
if (tmp & (1 << j)) {
sum += b[j + 1];
cur++;
}
}
bucket[sum][1] = true;
cnt[sum][1] = min(cur, cnt[sum][1]);
}
for (int i = 1; i <= 1e6; i++) {
if (bucket[i][0] && bucket[i][1]) {
ans = min(ans, cnt[i][0] + cnt[i][1]);
}
}
if (ans == INF) {
cout << "impossible" << '\n';
} else {
cout << ans << '\n';
}
return 0;
}
\(\text{100pts}\)
#include <bits/stdc++.h>
using namespace std;
static const int N = 150, INF = 0x3f3f3f3f, M = 1e6 + 50;
int n, m;
int a[N], b[N], f[M][2], sum[2];
int ans = INF;
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
memset(f, 0x3f, sizeof(f));
f[0][0] = f[0][1] = 0;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
sum[0] += a[i];
}
cin >> m;
for (int i = 1;i <= m; i++) {
cin >> b[i];
sum[1] += b[i];
}
for (int i = 1; i <= n; i++) {
for (int j = sum[0]; j >= a[i]; j--) {
f[j][0] = min(f[j][0], f[j - a[i]][0] + 1);
}
}
for (int i = 1; i <= m; i++) {
for (int j = sum[1]; j >= b[i]; j--) {
f[j][1] = min(f[j][1], f[j - b[i]][1] + 1);
}
}
for (int i = 1; i <= min(sum[0], sum[1]); i++) {
if (f[i][0] != INF && f[i][1] != INF) {
ans = min(ans, f[i][0] + f[i][1]);
}
}
if (ans == INF) {
cout << "impossible" << '\n';
} else {
cout << ans << '\n';
}
return 0;
}
T2
题意
给你一个二维平面内的 \(n\) 个矩形以及一个观测点 \(s(x, y)\),现有 \(q\) 个询问,每次询问给出一个整数 \(x\),问有多少个矩形满足存在一个矩形上的点使得其与观测点的曼哈顿距离恰好为 \(x\)。
\(n, q \le 10^5\)。
思路
考场上求曼哈顿距离的函数写假了,所以爆零了。虽然就是没假我也只能混到 \(\text{60pts}\)。
\(\text{30pts}\)
这部分数据保证 \(n \le 10\)。
由于 \(n\) 的范围极小,这部分乱搞都能过。
我们考虑求出观测点到每个矩形的最大曼哈顿距离与最小曼哈顿距离,然后在每次询问的时候暴力统计即可,时间复杂度 \(O(nq)\)。
那么如何计算这个最大最小距离呢?首先我们可以明确,最大距离一定是观测点到矩形四个顶点的曼哈顿距离的最大值,这个可以分类讨论证明。而最小值则要麻烦一些,它不仅可以是观测点到矩形四个顶点的曼哈顿距离的最小值,当其位于如下区域时,也可以是到矩形某条边长的最小值:
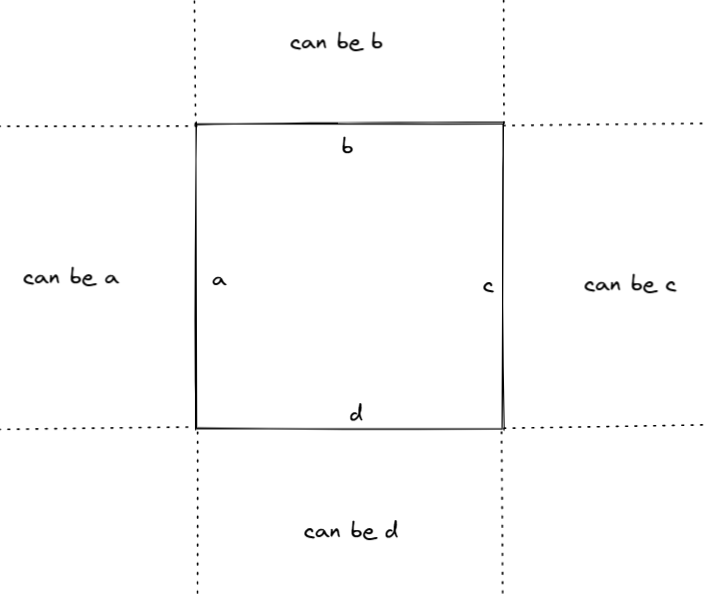
也就是说当观测点的横坐标或纵坐标与矩形的边有交集时,需要特殊处理。
\(\text{60pts}\)
另有 \(30\%\) 的数据保证 \(q \le 10\)。
做法同上,感觉这两个部分分的意义都不大。
\(\text{100pts}\)
这个数据范围,估摸着要么时间复杂度是 \(O(q \log n)\),要么就是线性的。
有了上边两个部分分,正解的思维难度其实应该也不大。
我们仍然考虑先求出观测点到每个矩形的最大曼哈顿距离与最小曼哈顿距离。每次询问时我们实际上是在求满足 \(\operatorname{minDis}_i \le x \le \operatorname{maxDis}_i\) 的 \(i\) 的数量。看到这坨东西,我们可以想到用一个权值线段树状物乱搞一下。在计算出第 \(i\) 个矩形的最大与最小距离时,我们把 \(\operatorname{minDis}_i \sim \operatorname{maxDis}_i\) 的这部分整体加 \(1\)。这样我们就将询问转化为了一个单点查询的问题,每次询问只需查下 \(x\) 所对应的权值就是答案,而这正是线段树以及树状数组擅长的。这样做的时间复杂度为 \(O(q \log 4 \times 10^6)\),后边这一坨是因为题目中明确规定矩形的横纵坐标不超过 \(2 \times 10 ^ 6\)。
你为这样就完了?不!由于这道题并没有边修改边询问,我们事实上可以用差分数组来代替线段树。设差分数组为 \(d\),那么当我们计算出矩形 \(i\) 的对应距离时,我们让 \(d_{\operatorname{minDis}_i}\) 自增,\(d_{\operatorname{maxDis}_i + 1}\) 自减即可。最后再求一遍前缀和,也能计算出这个权值数组。而此时询问就变成 \(O(1)\) 的了。总体时间复杂度为 \(O(n + q)\)。
代码
\(\text{30pts \& 60pts}\)
太简单了不给。
\(\text{100pts}\)
这里仅给出差分的写法的代码。
#include <bits/stdc++.h>
using i64 = long long;
static const int N = 1e5 + 50, INF = 0x3f3f3f3f, M = 4e6 + 50;
struct Bird {
int x1, y1, x2, y2;
};
void convert(Bird &i) {
if (i.x1 > i.x2) {
std::swap(i.x1, i.x2);
}
if (i.y1 > i.y2) {
std::swap(i.y1, i.y2);
}
return;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, q, x, y;
std::cin >> n >> q;
std::cin >> x >> y;
std::vector<Bird> bird(n);
std::vector<int> d(M);
for (auto &i : bird) {
std::cin >> i.x1 >> i.y1 >> i.x2 >> i.y2;
convert(i);
}
for (int i = 0; i < n; i++) {
int x1 = bird[i].x1, x2 = bird[i].x2;
int y1 = bird[i].y1, y2 = bird[i].y2;
int maxx = 0, minn = INF;
int d1 = std::abs(x - x1), d2 = std::abs(x - x2);
int d3 = std::abs(y - y1), d4 = std::abs(y - y2);
maxx = std::max(maxx, d1 + d3);
maxx = std::max(maxx, d2 + d4);
maxx = std::max(maxx, d1 + d4);
maxx = std::max(maxx, d2 + d3);
minn = std::min(minn, d1 + d3);
minn = std::min(minn, d2 + d4);
minn = std::min(minn, d1 + d4);
minn = std::min(minn, d2 + d3);
if (x >= x1 && x <= x2) {
if (y >= y1 && y <= y2) {
minn = 0;
} else {
minn = std::min(d3, d4);
}
} else if (y >= y1 && y <= y2) {
minn = std::min(d1, d2);
}
d[minn]++;
d[maxx + 1]--;
}
for (int i = 1; i < M; i++) {
d[i] += d[i - 1];
}
for (int i = 1; i <= q; i++) {
int u;
std::cin >> u;
std::cout << d[u] << '\n';
}
return 0;
}
T3
感谢 @_cyle_king 提供的题解。
题意
你有 \(n\) 种信件,第 \(i\) 种信件有一个长宽 \((x_i, y_i)\) 以及数量 \(cnt_i\)。现有 \(k\) 个大小可以任意指定的信封,你要把这 \(n\) 种信塞进信封。同一种信只能塞进同一个信封。设信封的长为 \(h\),宽为 \(w\),定义一个信封的未利用值为 \(\sum_{i} hw - x_i y_i\),其中 \(i\) 是这个信封中的信件。现在你要求所有信封未利用值之和的最小值。
注意,信不可以旋转,一个信封的长宽当然要比其中的任意一封信的长宽都不小。
\(k \le n \le 15\)。
思路
\(\text{30pts}\)
这部分数据保证 \(k = 1\) 或者 \(k = n\)。
当 \(k = 1\) 时,显然信封的长为所有信件中长的最大值,宽为所有信件中宽的最大值时,取得最优。
当 \(k = n\) 时,由于所有的信都可以单独放进一个信封,所以答案是 \(0\)。
\(\text{60pts or 70pts}\)
这部分数据保证 \(n \le 10\)。
考虑搜索,直接把当前信件的归属状态写进搜索的状态,爆搜就行了。
时间复杂度 \(O(玄学)\),如果剪枝剪的不好就是 \(\text{60pts}\),不然可以混到 \(\text{70pts}\)。
\(\text{100pts}\)
看着眼熟的数据范围,我们优先考虑状压 DP。
首先考虑对每个状态,即每个二进制数,预处理出一个 \(cost\) 值,代表这个状态只考虑这一部分的最小花费。
然后我们定义状态 \(f_{i, j}\) 为二进制状态为 \(i\),使用了 \(j\) 个信封时的最小花费,那么显然有方程如下:
边界是 \(f_{0, j} = 0, j \in [1, k]\)。
代码
这里仅给出 \(\text{100pts}\) 的代码。
\(\text{100pts}\)
#include <bits/stdc++.h>
using i64 = long long;
static const i64 INF = 0x3f3f3f3f3f3f3f3f;
struct Mail {
i64 x, y, cnt;
};
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
int n, k;
std::cin >> n >> k;
std::vector<Mail> a(n);
std::vector<i64> cost(1 << n | 1), maxX(1 << n | 1), maxY(1 << n | 1), num(1 << n | 1);
std::vector<std::vector<i64>> f(1 << n | 1);
for (auto &i : a) {
std::cin >> i.x >> i.y >> i.cnt;
}
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
if (!(i & (1 << j))) {
maxX[i | (1 << j)] = std::max(maxX[i | (1 << j)], a[j].x);
maxY[i | (1 << j)] = std::max(maxY[i | (1 << j)], a[j].y);
num[i | (1 << j)] = num[i] + a[j].cnt;
cost[i | (1 << j)] = cost[i] + a[j].x * a[j].y * a[j].cnt;
}
}
}
for (int i = 0; i < (1 << n); i++) {
cost[i] = num[i] * maxX[i] * maxY[i] - cost[i];
}
for (int i = 0; i < (1 << n); i++) {
f[i].resize(k + 1);
for (int j = 0; j <= k; j++) {
f[i][j] = INF;
}
}
for (int i = 1; i < (1 << n); i++) {
f[i][1] = cost[i];
}
for (int i = 1; i < (1 << n); i++) {
for (int j = 1; j < k; j++) {
for (int k = i; k; k = (k - 1) & i) {
f[i][j + 1] = std::min(f[i][j + 1], f[k][j] + cost[i ^ k]);
}
}
}
std::cout << f[(1 << n) - 1][k] << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号