2 月 22 日测试题解

T1

题意

给你一个 \(n \times m\) 的矩阵，每个格子的边长为 \(100\)，再给你 \(k\) 个特殊的格子，特殊的格子可以直接走对角线。现在问你从坐标为 \((1, 1)\) 的个子走到坐标为 \((n, m)\) 的格子的最短距离。

\(n, m \le 10^5\)，\(k \le 1000\)。

思路

考场上第一思路是这样的：把每个特殊的格子都拆成两个点，坐标为 \((i, j)\) 的点，我们就把它拆成 \((i, j)\) 与 \((i + 1, j + 1)\) 两个点，再把这两个点都重新赋一个编号，然后建图跑一遍 Dijkstra，时间复杂度 \(O(k \log k + k ^ 2 \log k)\)，是可以过的，至于后边这个 \(\log\) 是怎么来的，是因为我用了个 map 存点。

这道题其实是可以离散化再直接开二维数组，不用 map 的。虽然用了也能过，但是不用能降一只 \(\log\)。

然后正解是这样的：对于每个特殊的格子，我们把它们存到一个结构体里边排个序，排序规则是先按 \(x\) 坐标增序排，再按 \(y\) 降序排，然后做一遍 LIS，答案就是 \(100 \times (n + m) + (100\sqrt 2 - 200) \times len\)，其中 \(len\) 是你求出来的 LIS 长度。时间复杂度 \(O(k \log k)\)。

正确性其实不难证明。你要走出一条最短的路径，就是相当于在保证只向上走与只向右走的情况下，走最多的特殊格子，那么按照 \(x\) 升序就不难理解了。但是为什么要按 \(y\) 降序呢？是因为我们要保证在 \(x\) 坐标相同的情况下，先更新上边的点。

就比如说 \((1, 1)\) 与 \((1, 2)\) 两个点，如果你按照 \(y\) 升序排的话，那你得到的 LIS 长度是 \(2\)，但是根据题意，这个长度只能是 \(1\)，因为你无法从 \((1, 1)\) 这个格子走到 \((1, 2)\) 这个格子而不走回头路。注意，这里我们讨论的是格子，而不是点的坐标。

代码

我的代码：

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
#include <vector>
#include <map>
#include <cmath>

using namespace std;
using i64 = long long;

static const int N = 1e5 + 50, K = 1e3 + 50, INF = 0x3f3f3f3f;
static const double sq = sqrt(2);
int n, m, k;
double dis[10 * K];
bool vis[10 * K];
struct Path {
    int x, y;
    bool operator< (const Path &oth) const {
        if (x == oth.x) {
            return y < oth.y;
        }
        return x < oth.x;
    }
};
Path path[K];
vector<pair<int, double>> e[10 * K]; 
map<pair<int, int>, int> mp;
int cnt;

inline void add(int u, int v, double w) {
    return (void)(e[u].emplace_back(v, w));
}

void dijkstra() {
    priority_queue<pair<double, int>, vector<pair<double, int>>, greater<pair<double, int>>> pq;
    memset(vis, 0, sizeof(vis));
    pq.emplace(0, 0);
    for (int i = 1; i <= cnt + 1; i++) {
        dis[i] = INF;
    }
    dis[0] = 0;
    while (!pq.empty()) {
        auto i = pq.top();
        pq.pop();
        int u = i.second;
        if (vis[u]) {
            continue;
        }
        vis[u] = true;
        for (auto j : e[u]) {
            int v = j.first;
            double w = j.second;
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                pq.emplace(dis[v], v);
            }
        }
    }
    return;
}

void getNo() {	
    for (int i = 1; i <= k; i++) {
        int x = path[i].x, y = path[i].y;
        if (!mp.count(make_pair(x, y))) mp[make_pair(x, y)] = ++cnt;
        if (!mp.count(make_pair(x + 1, y + 1))) mp[make_pair(x + 1, y + 1)] = ++cnt;
    }
    
    return;
}

void build() {
    add(0, cnt + 1, n + m + 2);
    
    for (int i = 1; i <= k; i++) {
        int x = path[i].x, y = path[i].y;
        add(0, mp[make_pair(x, y)], abs(x - 1 + y - 1));
        add(0, mp[make_pair(x + 1, y + 1)], abs(x + y));
    }
    
    for (int i = 1; i <= k; i++) {
        int x = path[i].x, y = path[i].y;
        add(mp[make_pair(x, y)], mp[make_pair(x + 1, y + 1)], sq);
        for (int j = 1; j < i; j++) {
            int dx = path[j].x, dy = path[j].y;
            add(mp[make_pair(dx, dy)], mp[make_pair(x, y)], abs(x - dx) + abs(y - dy));
            add(mp[make_pair(dx + 1, dy + 1)], mp[make_pair(x + 1, y + 1)], abs(x - dx) + abs(y - dy));
            add(mp[make_pair(dx + 1, dy + 1)], mp[make_pair(x, y)], abs(x - dx - 1) + abs(y - dy - 1));
            add(mp[make_pair(dx, dy)], mp[make_pair(x + 1, y + 1)], abs(x - dx + 1) + abs(y - dy + 1));
        }
    }
    
    for (int i = 1; i <= k; i++) {
        int x = path[i].x, y = path[i].y;
        add(mp[make_pair(x, y)], cnt + 1, abs(n + m + 2 - x - y));
        add(mp[make_pair(x + 1, y + 1)], cnt + 1, abs(n + m - x - y));
    }
    
    return;
}

int main() {	
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> n >> m >> k;
    for (int i = 1; i <= k; i++) {
        cin >> path[i].x >> path[i].y;
    }
    
    sort(path + 1, path + k + 1);
    getNo();
    build();
    dijkstra();
    
    cout << (int) round(100 * dis[cnt + 1]) << '\n';
    
    return 0;
}

正解：

#include <bits/stdc++.h>

using namespace std;

static const int K = 1e3 + 50, N = 1e5 + 50;
struct Point {
    int x, y;
    bool operator< (const Point &oth) const {
        if (x == oth.x) {
            return y > oth.y;
        } else {
            return x < oth.x;
        }
    }
} point[K];
map<pair<int, int>, int> mp;
int n, m, k;
int f[K], len = 1;
vector<int> c[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m >> k;
    for (int i = 1; i <= k; i++) {
        cin >> point[i].x >> point[i].y;
    }

    sort(point + 1, point + k + 1);

    memset(f, 0x3f, sizeof(f));
    for (int i = 1; i <= k; i++) {
        int pos = lower_bound(f + 1, f + k + 1, point[i].y) - f;
        f[pos] = point[i].y;
        len = max(len, pos);
    }

    cout << (int) round(100 * (n + m) + (sqrt(2) - 2) * 100 * len) << '\n';

    return 0;
}

T2

题意

给你 \(n\) 个组件，问你是否能用它们拼成一个正方形。若能，输出一种方案，否则输出 \(-1\)。

\(n \le 5\)，每个组件的长宽不超过 \(5\)。

思路

一看数据范围，显然的爆搜。

我们首先计算出所有组件中的非空点数之和，如果其不是一个完全平方数，那么肯定拼不出一个正方形，否则我们就可以得到正方形的边长。

然后开始直接开始搜索就好了。一个剪枝都不用加，搜到了就输出然后 exit(0) 就好了。

我写了两个辅助函数来简化搜索流程，事实证明非常有效，直接省去了许多调试的步骤。

代码

#include <iostream>
#include <cmath>

using namespace std;

const int N = 30;
struct Component {
    int x, y;
    bool a[N][N];
} comp[N];
int n, a[N][N], m;
int all;

bool put(int id, int sx, int sy, int cnt) {
    int x = comp[id].x, y = comp[id].y;
    for (int i = 1; i <= x; i++) {
        for (int j = 1; j <= y; j++) {
            if (comp[id].a[i][j]) {
                int dx = sx + i - 1, dy = sy + j - 1;
                if (a[dx][dy] != 0 && a[dx][dy] != cnt) {
                    return false;
                } else if (dx > m || dy > m) {
                    return false;
                }
            }
        }
    }
    for (int i = 1; i <= x; i++) {
        for (int j = 1; j <= y; j++) {
            if (comp[id].a[i][j]) {
                int dx = sx + i - 1, dy = sy + j - 1;
                a[dx][dy] = cnt;
            }
        }
    }
    return true;
}

void clear(int cnt) {
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i][j] == cnt) a[i][j] = 0;
        }
    }
    return;
}

void dfs(int state, int cnt) {
    if (state == (1 << n) - 1) {
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= m; j++) {
                cout << a[i][j];
            }
            cout << '\n';
        }
        exit(0);
    }
    for (int i = 1; i <= n; i++) {
        if (state & (1 << (i - 1))) {
            continue;
        }
        for (int j = 1; j <= m; j++) {
            for (int k = 1; k <= m; k++) { 
                if (put(i, j, k, cnt + 1)) {
                    dfs(state | 1 << (i - 1), cnt + 1);
                    clear(cnt + 1);
                }
            }
        }
    }
    return;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> comp[i].x >> comp[i].y;
        for (int j = 1; j <= comp[i].x; j++) {
            for (int k = 1; k <= comp[i].y; k++) {
                char c;
                cin >> c;
                comp[i].a[j][k] = (c == '1');
                all += (c == '1');
            }
        }
    }
    
    m = sqrt(all);
    if (m * m != all) {
        cout << -1 << '\n';
        return 0;
    }
    
    dfs(0, 0);
    
    cout << -1 << '\n';
    
    return 0;
}

T3

题意

题意比较复杂，我不知道能不能说清楚。

你要为一场比赛安排赛程表。有 \(n\) 支参赛队伍，比赛会持续 \(n\) 天，每天会有 \(n - 1\) 支队伍参赛，剩余一支队伍轮休，现在给出第 \(m\) 支队伍的赛程安排，即每一天的对手是谁，问你第 \(t\) 天的赛程安排，即第 \(t\) 天每支队伍的对手。若这支队伍的对手是他自己，则表示这支队伍当天轮休。

\(n \lt 500\)。

思路

考场上是这样想的：我们可以通过如下方法构造出一张绝对合法的赛程表，直接说明不太好说，举个例子就明白了。

天数 \ 队伍	1	2	3
一	3	1	2
二	2	3	1
三	1	2	3

想必聪明的大家都看懂了怎么构造这个表格吧？我们可以看出，第 \(i\) 天第 \(j\) 支队伍的对手就是 \(((n - i - j + 1) \bmod n) + 1\)。可以证明这样构造出来的表绝对合法。

那么剩下的部分呢？由于题目已经给出了第 \(m\) 支队伍的对手，所以我们可以把这 \(n\) 支队伍重新编号，映射到上边这张表中。具体的做法就是先根据第 \(m\) 支队伍的轮休日期确定其应该被编为几号，然后再将其他的队伍根据表中的赛程安排映射上去。由于我们要求的是第 \(t\) 天的全部赛事，所以我们再在表中找到第 \(t\) 天第 \(m\) 支队伍的对手，这样我们就能够确定其在表中对应的是哪一天，再在输出时将其转为原本的队伍编号。

时间复杂度为 \(O(n^2)\)，好像还有 \(O(n)\) 的解法，但是我不会。

代码

#include <iostream>

using namespace std;
using i64 = long long;

static const int N = 600;
int n, m, t;
int bucket[N], table[N][N];
int opposite[N], pivot, tmp;
int mp[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> n >> m >> t;
    for (int i = 1; i <= n; i++) {
        cin >> opposite[i];
        if (m == opposite[i]) {
            pivot = i;
        }
    }
    
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            table[i][j] = ((n - j - i + 1) % n + n) % n + 1;
        }
    }
    
    for (int i = 1; i <= n; i++) {
        if (table[i][pivot] == i) {
            bucket[m] = i;
            tmp = i;
            break;
        }
    }
    for (int i = 1; i <= n; i++) {
        bucket[opposite[i]] = table[tmp][i];
        mp[table[tmp][i]] = opposite[i];
    }
    for (int i = 1; i <= n; i++) {
        if (bucket[opposite[t]] == table[i][bucket[m]]) {
            tmp = i;
            break;
        }	
    }
    for (int i = 1; i <= n; i++) {
        cout << mp[table[tmp][mp[i]]] << ' ';
    }
    
    return 0;
}

T4

题意

一个长度为 \(n\) 的环，环上的第 \(i\) 个点要求涂有 \(a_i\) 种颜色，并且任意两个相邻的点不能涂有相同的颜色，求最少需要的颜色数量。

\(n \le 20000\)。

思路

第一眼看题：这不显然的贪心吗？？？？
我们考虑求出 \(a\) 中的最大邻项之和，然后这个东西貌似就是答案？
三分钟写出代码，小样例、大样例全过。洋洋得意的以为这道题如此简单，但其实已经掉进了坑里。

贪心是错的。我们举个很简单的例子：

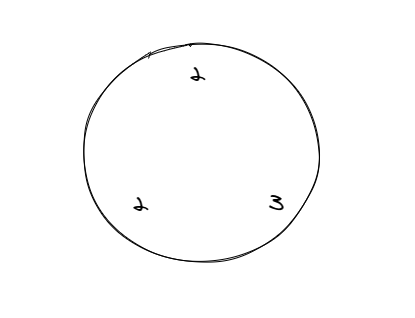
即 \(2 \, 3 \, 2\) 这个序列。贪心的结果是 \(5\)，但是显然最少需要 \(7\) 种颜色才满足要求。

事实上这是一道结论题。

我们记上边贪心的结果为 \(T\)，那么最终的答案就是 \(\max(T, \lceil{\frac{\sum_{i = 1}^n a_i}{\lfloor\frac{n}{2}\rfloor}}\rceil)\)。证明我是真的不会，只能贴个链接在这。

代码

#include <bits/stdc++.h>

using namespace std;
using i64 = long long;

static const int N = 1e5 + 50;
int n;
i64 a[N], sum, maxx;

int main() {
  ios::sync_with_stdio(false);
  cin.tie(0), cout.tie(0);
  
  cin >> n;
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
    sum += a[i];
  }

  for (int i = 1; i < n; i++) {
    maxx = max(maxx, a[i] + a[i + 1]);
  }
  maxx = max(maxx, a[1] + a[n]);

  cout << max(maxx, (i64) ceil((double) sum / (n >> 1))) << '\n';

  return 0;
}

posted @ 2023-02-24 21:42 ForgotDream 阅读(26) 评论(0) 收藏举报

刷新页面返回顶部

forgot-dream

2 月 22 日测试题解

2 月 22 日测试题解

T1

题意

思路

代码

T2

题意

思路

代码

T3

题意

思路

代码

T4

题意

思路

代码

公告