吴恩达神经网络和深度学习——浅层神经网络

一、浅层神经网络

1. 神经网络的表示

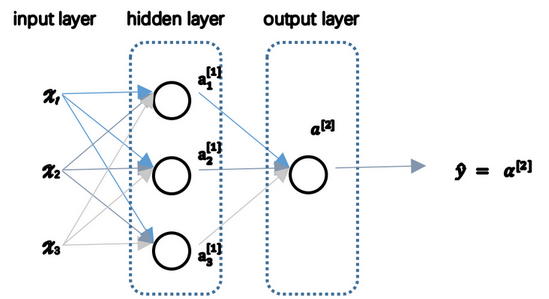
单隐藏层神经网络是典型的浅层神经网络，两层神经网络，从隐藏层开始到输出层的层数是神经网络的总层数

x表示神经网络的输入层
后续的是隐藏层，第l层的权重维度的行等于l层神经元的个数，列等于层神经元的个数；第层常数项维度的行等于层神经元的个数，列始终为1
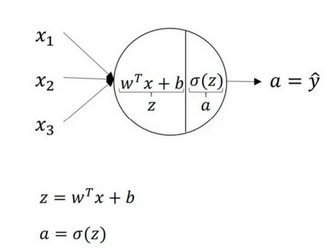
隐藏层会有激活函数
最后一层是输出层，产出预测值

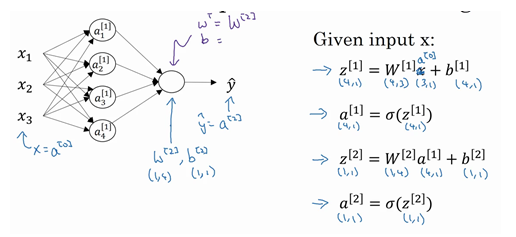
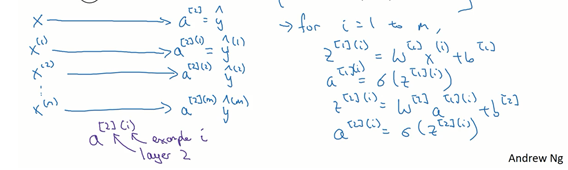
向量化：

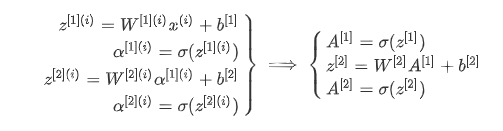
2. 激活函数

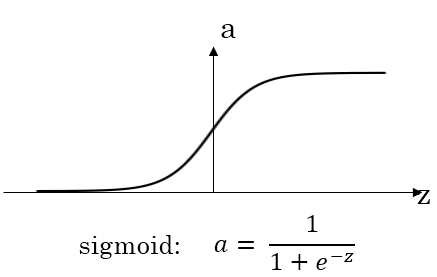
如果输出是0、1值（二分类问题），则输出层选择sigmoid函数，然后其它的所有单元都选择Relu函数
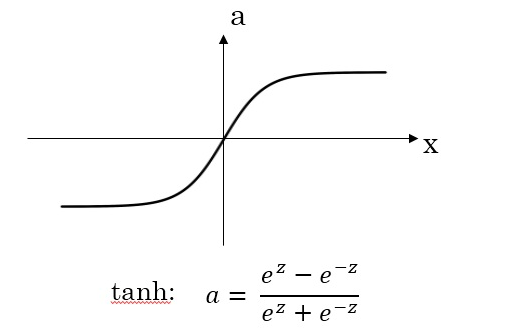
tanh激活函数：tanh是非常优秀的，几乎适合所有场合。函数的取值范围在[−1,+1]之间，隐藏层的输出被限定在[−1,+1]之间，可以看成是在0值附近分布，均值为0。这样从隐藏层到输出层，数据起到了归一化（均值为）的效果
sigmoid函数和tanh函数两者共同的缺点是，在z $特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于0，导致降低梯度下降的速度，造成梯度消失$
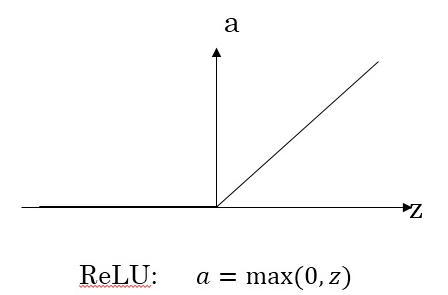
如果在隐藏层上不确定使用哪个激活函数，那么通常会使用Relu激活函数。有时，也会使用tanh激活函数，Relu的优点是：只要z $是正值的情况下，导数恒等于1常数，有足够的隐藏层使得z>0，当z 是负值的时候，导数恒等于0，神经元此时不会训练，加快了训练过程，在实践中，z 等于0时假设导数是1或者0效果都可以$
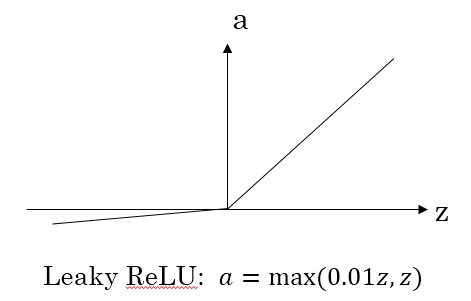
Leaky Relu，当z $是负值时，这个函数的值不是等于0，而是轻微的倾斜，$ 这个函数通常比Relu激活函数效果要好，尽管在实际中Leaky ReLu使用的并不多
在z $的区间变动很大的情况下， ReLu 在程序实现就是一个 if-else 语句，而 sigmoid 函数需要进行浮点四则运算，在实践中，使用 ReLu 激活函数神经网络通常会比使用 sigmoid 或者 tanh 激活函数学习的更快$

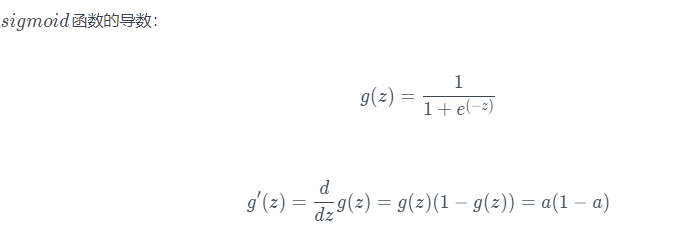
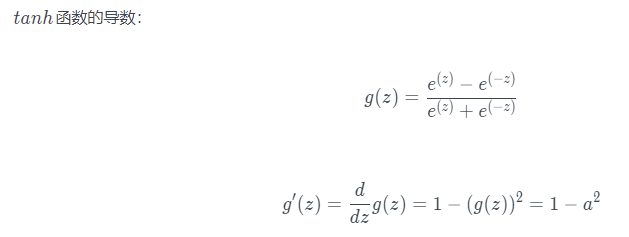
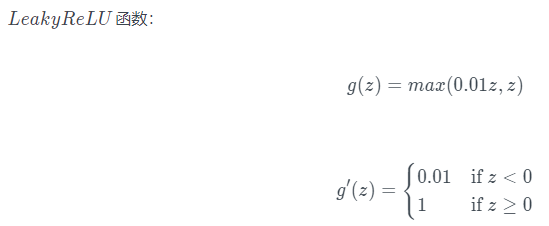
3. 选用非线性激活函数的原因

多层隐藏层的神经网络如果使用线性函数作为激活函数，最后的输出还是线性模型，深层神经网络不起作用
如果是预测问题而不是分类问题，输出是连续的情况下，输出层的激活函数可以使用线性函数。如果输出恒为正值，则也可以使用ReLU激活函数

4. 神经网络的梯度下降

　　这些都是针对所有样本进行过向量化，Y $是1Xm 的矩阵；这里 np.sum 是python的numpy命令， axis=1 表示水平相加求和， keepdims 是防止 python 输出那些古怪的秩数(n，) ，确保阵矩阵db [2] 这个向量输出的维度为($ $n,1) 这样标准的形式.还有一种防止 python 输出奇怪的秩数，需要显式地调用 reshape 把 np.sum 输出结果写成矩阵形式。$

$5.随机初始化$

symmetry breaking problem：对于一个神经网络，如果你把权重或者参数都初始化为0，使得部分神经元完全一样，完全对称，也就意味着经过每次训练的轮迭代，他们进行同样的计算，隐藏层设置多个神经元就没有意义，梯度下降将不会起作用
随机初始化方法：

W_1 = np.random.randn((2,2))*0.01
b_1 = np.zero((2,1))
W_2 = np.random.randn((1,2))*0.01
b_2 = 0

　　让比较小，是因为如果使用sigmoid函数或者tanh函数作为激活函数的话，W比较小，得到的|z|也比较小（靠近零点），而零点区域的梯度比较大，这样能大大提高梯度下降算法的更新速度，尽快找到全局最优解；如果W较大，得到的|z|也比较大，附近曲线平缓，梯度较小，训练过程会慢很多

　　如果激活函数是ReLU或者LeakyReLU函数，则不需要考虑这个问题

posted @ 2023-02-24 14:38 forever_fate 阅读(219) 评论(0) 收藏举报

刷新页面返回顶部