java二叉树的遍历(1)
树(tree)是一种抽象数据类型(ADT),用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点通过连接它们的边组成一个具有层次关系的集合
-
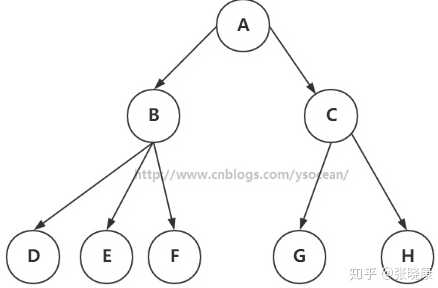
节点:上图的圆圈,比如A,B,C等都是表示节点。节点一般代表一些实体,在java面向对象编程中,节点一般代表对象。
-
边:连接节点的线称为边,边表示节点的关联关系。一般从一个节点到另一个节点的唯一方法就是沿着一条顺着有边的道路前进。在Java当中通常表示引用。
-
每个节点最多只能有两个子节点的一种形式称为二叉树
一、树的基本概念
-
-
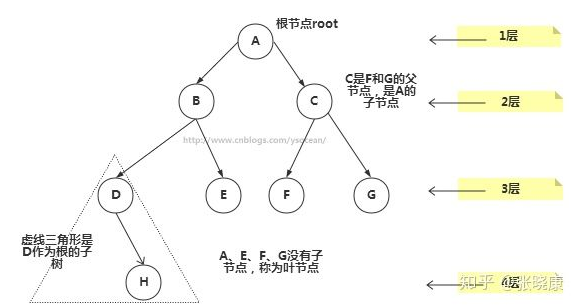
根:树顶端的节点称为根。一棵树只有一个根,如果要把一个节点和边的集合称为树,那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
-
父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;B是D的父节点。
-
子节点:一个节点含有的子树的根节点称为该节点的子节点;D是B的子节点。
-
兄弟节点:具有相同父节点的节点互称为兄弟节点;比如上图的D和E就互称为兄弟节点。
-
叶节点:没有子节点的节点称为叶节点,也叫叶子节点,比如上图的H、E、F、G都是叶子节点。
-
子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中。
-
节点的层次:从根开始定义,根为第一层,根的子节点为第二层,以此类推。
-
深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
-
高度
二、二叉树的遍历
-
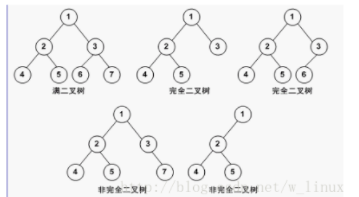
二叉树:每个节点最多只有两个子节点的树
-
如果二叉树的所有叶子节点都在最后一层,并且节点总数= 2^n -1,n 为层数,则该树为满二叉树
-
如果二叉树的所有叶子节点都在最后一层或倒数第二层,并且最后一层的叶子节点在左边连续,倒数第二层的叶子节点在右边连续,则称为完全二叉树
- 二叉树的遍历方式有三种:
-
-
中序遍历: 左,根,右
-
-
public class TreeNodeTest { public static void main(String[] args) { int[] arr={5,4,7,9,2,6,3}; TreeNode tree = new TreeNode(); for (int i=0;i<arr.length;i++){ tree.add(new Node(arr[i])); } } } class TreeNode{ Node root;//根节点 public TreeNode() { } public void add(Node node){ if (node==null) return; if (root==null) {root=node;return;} else root.add(node); } public void prefix() { if (root==null) return; else root.prefix(); } } class Node{ int val; //节点值 Node left;// 左节点 Node right; // 右节点 public Node(int val) { this.val = val; } public void add(Node node) { if (node==null)return; if (node.val<val) { if (left==null){left=node;return;} else left.add(node);} else { if(right==null) {right=node;return;} else right.add(node); } }
}
//TreeNode类下 //前序递归遍历 public void preOrder() { if (this.root!=null) this.root.preOrder(); else System.out.println("根节点为空"); } //中序递归遍历 public void infixOrder() { if (this.root!=null) this.root.infixOrder(); else System.out.println("根节点为空"); } //后序递归遍历 public void postOrder() { if (this.root!=null) this.root.postOrder(); else System.out.println("根节点为空"); } //Node类下 //前序递归遍历 public void preOrder() { System.out.print(this.val+ " "); if (this.left!=null) this.left.preOrder(); if (this.right!=null)this.right.preOrder(); } //中序递归遍历 public void infixOrder() { if (this.left!=null) this.left.infixOrder(); System.out.print(this.val+ " "); if (this.right!=null)this.right.infixOrder(); } //后序递归遍历 public void postOrder() { if (this.left!=null) this.left.postOrder(); if (this.right!=null)this.right.postOrder(); System.out.print(this.val+ " "); }
四、非递归前中后序遍历
- 前序遍历思路:
- 根节点入栈
- 判断栈是否为空,如果不为空,弹出栈顶元素并打印
- 如果有右子树,压栈
- 如果有左子树,压栈
public void prefix() { Stack<Node> s= new Stack<>(); s.push(this); while (!s.isEmpty()){ Node node = s.pop(); System.out.print(node.val+"-->"); if(node.right!=null) s.push(node.right); if(node.left!=null) s.push(node.left); } }
- 中序遍历思路:
-
根节点入栈
-
如果节点不为空,压栈,沿着左子树走一步
-
如果节点为空,则出栈,打印,沿着右子树走一步
-
-
//中序遍历 public void infixOrder() { //非递归 Stack<Node> s=new Stack<>(); Node node= this; while (!s.isEmpty()||node!=null){ if (node!=null){ s.push(node); node=node.left; } else { node=s.pop(); System.out.print(node.val+ " "); node=node.right; } } }
- 后序遍历思路:
-
申请两个栈s1,s2,头节点入栈s1
-
如果栈s1不为空,执行以下操作:弹出一个元素,入栈s2,
-
如果该节点左孩子不空,入栈s1,如果该节点右孩子不空入栈s1
-
-
public void postOrder() { //非递归 Stack<Node> s1=new Stack<>(); Stack<Node> s2=new Stack<>(); s1.push(this); while(!s1.isEmpty()){ Node node = s1.pop(); s2.push(node); if (node.left!=null) s1.push(node.left); if (node.right!=null) s1.push(node.right); } while (!s2.isEmpty()) System.out.print(s2.pop().val+ " "); // 一种栈实现 /* Stack<Node> s=new Stack<>(); Node node= this; Node lastnode= null; while (node!=null){ s.push(node); //将所有左节点入栈 node=node.left; } while(!s.isEmpty()){ node=s.pop(); //一个根节点被访问的前提是:无右子树或右子树已被访问过 if (node.right!=null&&node.right!=lastnode){ s.push(node); node=node.right; while (node!=null) { s.push(node); node=node.left;} } else { System.out.print(node.val+ " "); lastnode=node; } } */ }
五、前中序查找
- 前序查找:
- 先判断当前节点值是否为查找值,如果是返回当前节点
- 判断当前节点的左子节点是否为空,如果不为空,左子树递归前序查找
- 如果左递归返回的值不为空,说明找到,返回该节点
- 否则判断当前节点是否有右子节点,如果有,右子树递归前序查找
- 中序查找:
- 判断当前节点的左子节点是否为空,如果不为空,左子树递归中序查找
- 如果左递归返回的值不为空,说明找到,返回该节点
- 否则判断当前节点值是否为查找值,如果是返回当前节点
- 否则判断当前节点是否有右子节点,如果有,右子树递归中序查找
- 后序递归查找
- 判断当前节点的左子节点是否为空,如果不为空,左子树递归后序查找
- 如果左递归返回的值不为空,说明找到,返回该节点
- 否则判断当前节点是否有右子节点,如果有,右子树递归后序查找
- 如果右递归返回的值不为空,说明找到,返回该节点
- 否则判断当前节点值是否为查找值,如果是返回当前节点
//前序递归查找 public TreeNode preOrderSearch(int val) { System.out.println("前序递归查找"); if(this.val==val) {return this;} TreeNode node = null; if (this.left!=null){node=this.left.preOrderSearch(val);} if (node!=null) return node; //1.左递归前序查找,找到结点,则返回,否继续判断, //2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找 if (this.right!=null){node=this.right.preOrderSearch(val);} return node; } //中序递归查找 public TreeNode infixOrderSearch(int val) { TreeNode node = null; //1.左递归前序查找,找到结点,则返回,否继续判断, if (this.left!=null){node=this.left.infixOrderSearch(val);} if (node!=null) return node; System.out.println("中序递归查找"); if(this.val==val) {return this;} //2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找 if (this.right!=null){node=this.right.infixOrderSearch(val);} return node; } //后序递归查找 public TreeNode postOrderSearch(int val) { TreeNode node = null; //1.左递归前序查找,找到结点,则返回,否继续判断, if (this.left!=null){node=this.left.postOrderSearch(val);} if (node!=null) return node; if (this.right!=null){node=this.right.postOrderSearch(val);} if (node!=null) return node; System.out.println("后序递归查找"); if(this.val==val) {return this;} return node; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号