java基础---数组的查找算法(2)

一、查找的基本概念

查找分为有序查找和无序查找，这里均以数组为对象，有序查找指的是数组元素有序排列，无序查找指的是数组元素有序或无序排列

平均查找长度（Average Search Length，ASL）：和指定查找元素key进行比较的表中数据的个数的期望值

- 对于含有n个数据元素的查找表，查找成功的平均查找长度为：ASL = Pi*Ci的和。
- Pi：查找表中第i个数据元素的概率。
- Ci：找到第i个数据元素时已经比较过的次数。
查找分类：线性查找（顺序查找）、二分查找（折半查找）、插值查找、斐波那契查找、分块查找、哈希查找、二叉树查找
查找性能从慢到快：
- 顺序查找，时间复杂度O(N)
- 分块查找，时间复杂度O(logN+N/m);
- 二分查找，时间复杂度O(logN)
- Fibonacci查找，时间复杂度O(logN)
- 插值查找，时间复杂度O(log(logN))
- 哈希查找，时间复杂度O(1)

二、线性查找

　　顺序查找适合于存储结构为顺序存储或链接存储的线性表，即查找对象存储空间连续

时间复杂度为O(n)
查找成功时的平均查找长度为：（假设每个数据元素的概率相等） ASL =(1+2+3+…+n)/n = (n+1)/2 ;
当查找不成功时，需要n+1次比较，时间复杂度为O(n);

package Search;

import java.util.ArrayList;
import java.util.List;

public class LinearSearch {

    public static void main(String[] args) {
        int[] arr={1,9,19,0,-2,9,43};
        System.out.println(firstlinearSearch(arr,-2));
        System.out.println(lastlinearSearch(arr,-1));
        System.out.println(repeatlinearSearch(arr,9));
    }
    //返回顺序查找第一次找到的下标位置
    private static int firstlinearSearch(int[] arr, int key) {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == key) {
                return i;
            }
        }
        return -1;}
    //返回顺序查找最后一次找到的下标位置
        private static int lastlinearSearch(int[] arr, int key) {
        int index=-1;
            for (int i = 0; i < arr.length; i++) {
                if (arr[i] == key) {
                    index=i;
                }
            }
            return index;
        }
    //返回所有重复的元素下标
    private static List<Integer> repeatlinearSearch(int[] arr, int key) {
        List<Integer> list= new ArrayList<>();
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == key) {
                list.add(i);
            }
        }
        return list;
    }
}

三、二分查找

折半查找，属于有序查找算法。这里的有序是指查找的数组元素是有序排列的
用给定值k先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表，
递归思想
- 递归条件：查找值>中间值，向右递归；查找值<中间值，向左递归
- 终止条件：查找值=中间值，返回中间值坐标；查找区间溢出（left>right）, 返回-1；
- 如果有溢出，说明left+right>Integer.MAX_VALUE
- 对待有重复元素的数组：当查找值=中间值，在中间值坐标向左向右遍历（temp>left && arr[temp]==arr[mid];temp<right&&arr[temp]=arr[mid]），直到找到与中间值不相等的元素，顺序添加到表中
非递归思想，直接用循环while（left<right）
- 查找值>中间值， left=mid; 查找值<中间值， right=mid;
- 终止条件：查找值=中间值，返回中间值坐标；查找区间溢出（left>right）, 返回-1；
最坏情况下，关键词比较次数为log2(n+1)，且期望时间复杂度为O(log2n)；
折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。
但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用

package Search;
import java.util.ArrayList;
import java.util.List;
public class BinarySearch {
    public static void main(String[] args) {
        int[] arr={1,2,3,4,5,6,7,8,8,8,10,23,45,67,89,100,101};
        System.out.println(binarysearch(arr,0,arr.length-1,8));
        System.out.println(repeatbinarysearch(arr,0,arr.length-1,8));
        System.out.println(bobinarysearch(arr,0,arr.length-1,8));
    }

    //返回所有与查找元素相同的所有元素下标
    private static List<Integer> repeatbinarysearch(int[] arr, int left, int right, int key) {
        if (left>right) return new ArrayList<>();
        List<Integer> list= new ArrayList<>();
        int mid=(left+right)/2;
        if (arr[mid]<key){
            return repeatbinarysearch(arr,mid+1,right,key);
        }else if (key<arr[mid]){
            return repeatbinarysearch(arr,left,mid-1,key);
        }else {
            int temp=mid-1;
            while (true) {
                if (temp < left || arr[temp] != arr[mid]) {
                    break;
                }
                else temp--;
            }
            for (int i= temp+1;i<mid;i++){
                list.add(i);
            }
            temp=mid;
            while (true) {
                if (temp >right || arr[temp] != arr[mid]) {
                    break;
                }
                else {list.add(temp);
                temp++;}
            }
           return  list;
        }
    }

    //不一定返回的是顺序第一次找到的下标
    private static int  binarysearch(int[] arr, int left, int right, int key) {
        if (left>right) return -1;
        int mid= (left+right)/2;
        if (arr[mid]<key){
            return binarysearch(arr,mid+1,right,key);
        }else if (key < arr[mid]){
           return  binarysearch(arr,left,mid-1,key);
        }else  return mid;
    }
    //非递归
   private static int bobinarysearch(int[] arr, int left, int right, int key) {
        if (arr==null||arr.length==0) return  -1;
        if (left>right) return  -1;
        int mid;
        while (left<right){
            mid=left+(right-left)/2;
            if (arr[mid]==key)return mid;
            else if(arr[mid]<key) left=mid+1;
            else right=mid-1;
        }
        return -1;
    }
}

四、插值查找

基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率，属于有序查找
查找成功或者失败的时间复杂度均为O(log2(log2n))
对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。
反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。
与二分查找唯一的不同点是中值的选择利用了自适应算法 mid=left+(right-left) *(key-arr[left])/(arr[right]-arr[left])

package Search;

import java.util.ArrayList;
import java.util.List;

public class InsertValueSearch {
    public static void main(String[] args) {
        int[] arr=new int[100];
        for (int i=0;i<arr.length;i++){
            arr[i]=i+1;
        }
        arr[8]=8;
        System.out.println(insertsearch(arr,0,arr.length-1,8));
        System.out.println(repeatinsertsearch(arr,0,arr.length-1,8));

    }

    private static List<Integer> repeatinsertsearch(int[] arr, int left, int right, int key) {
        if (left > right) return new ArrayList<>();
        List<Integer> list = new ArrayList<>();
        //唯一的不同点是中值的选择利用了自适应算法
        //low + (high-low) * (value-a[low]) / (a[high]-a[low]);
        int mid = left + (right - left) * (key - arr[left]) / (arr[right] - arr[left]);
        if (arr[mid] < key) {
            return repeatinsertsearch(arr, mid + 1, right, key);
        } else if (key < arr[mid]) {
            return repeatinsertsearch(arr, left, mid - 1, key);
        } else {
            int temp = mid - 1;
            while (true) {
                if (temp < left || arr[temp] != arr[mid]) {
                    break;
                } else temp--;
            }
            for (int i = temp + 1; i < mid; i++) {
                list.add(i);
            }
            temp = mid;
            while (true) {
                if (temp > right || arr[temp] != arr[mid]) {
                    break;
                } else {
                    list.add(temp);
                    temp++;
                }
            }
            return list;
        }
    }
    private static int  insertsearch(int[] arr, int left, int right, int key) {
            if (left>right) return -1;
            int mid=left+(right-left)*(key-arr[left])/(arr[right]-arr[left]) ;
            if (arr[mid]<key){
                return insertsearch(arr,mid+1,right,key);
            }else if (key < arr[mid]){
                return  insertsearch(arr,left,mid-1,key);
            }else  return mid;
        }
    }

五、斐波那契查找

黄金分割比例：要求开始表中记录的个数为某个斐波那契数小1，n=F(k)-1;
最坏情况下，时间复杂度为O(log2n)，且其期望复杂度也为O(log2n)。
生成的数组长度是f[k]-1而不是f[k]
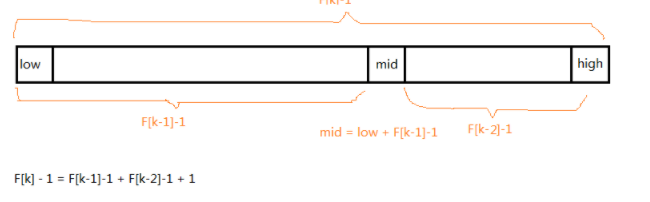
f[k]-1=f[k-1]-1+f[k-2]-1+1，只要顺序表的长度为f[k]-1，就可以将其分为左右两端，左边端为f[k-1]-1，右边为f[k-2]-1，中间值mid= left+ f[k-1]-1

步骤:

生成一个斐波那次数组，这个数组的长度为f[k]-1
生成的数组很可能比要比较的数组元素大，因此要进行元素赋值和填充

package Search;

import java.util.Arrays;
import java.util.List;

public class FibonacciSearch {
    public static void main(String[] args) {
        int[] arr={1,2,3,4,5,6,7,8,8,8,10,23,45,67,89,100,101};
        System.out.println(fibonacci(arr,100));
      //  System.out.println(repeatfibonacci(arr,8));
    }
    //构造斐波那次数组
    private static int[] fib(int size) {
        int[] f=new int[size];
        f[0]=1;
        f[1]=1;
        for (int i=2;i<f.length;i++){
            f[i]=f[i-1]+f[i-2];
        }
        return  f;
    }
    private static int fibonacci(int[] arr,  int key) {
         int low = 0;
         int high = arr.length-1;
         int f[]= fib(arr.length);
        //此时已经找到比high大的那个斐波那次点
        int k=0;
        while (high-low>f[k]-1) k++;
         //复制一份arr，但长度可能有扩充
        int[] temp = Arrays.copyOf(arr, f[k]);
        //把扩充后的元素都赋值为当前数组的最大元素
       for (int i=high;i<temp.length;i++) temp[i]=arr[high];
       int mid=0;
       while (low<=high){
           mid= low + f[k-1]-1;
           //此时f[k-1]指代的是左半部分
           if (temp[mid]>key){
               high=mid-1;
               k--;
           } //f[k-2]指代右半部分
           else if (temp[mid] < key){
               low=mid+1;
               k-=2;
           }
           else  return Math.min(mid, high);
       }
        return -1;
    }
}

六、分块查找

分块查找是结合二分查找和顺序查找的一种改进方法。在分块查找里有索引表和分块的概念。索引表就是帮助分块查找的一个分块依据，索引表是二分查找，而后进行顺序查找
分块查找只需要索引表有序，类似于哈希表，但又不如散列表好用。假设每个分块的长度为s，则分块查找的时间复杂度可以近似为：，即
分块查找算法的查找算法并不复杂，复杂的时索引表的建立与维护，当元素加、减、修改时，如何保证各个分块之间依旧相对有序且各个分块的大小均匀，是分块查找算法最大的挑战

posted @ 2020-09-16 00:03 forever_fate 阅读(688) 评论(0) 收藏举报

刷新页面返回顶部

java基础---数组的查找算法(2)

一、查找的基本概念

二、 线性查找

三、 二分查找

四、 插值查找

五、 斐波那契查找

六、分块查找

公告

二、线性查找

三、二分查找

四、插值查找

五、斐波那契查找