SPSS-回归

1、一元回归

 

 

一元线性回归分析、多元线性回归分析

【一元线性回归分析】

已经某变量取值，如果想要用它得到另一个变量的预测值

自变量或预测变量、因变量或标准变量

1. 目的：根据某自变量取值得到因变量的预测值

2. 所需数据：
   因变量（连续变量）+自变量（连续变量、二分变量）

3. 假设条件：
   a. 观测值独立
   b. 两个变量服从正态分布：总体中每一变量的取值都要服从正态分布，而且对某一变量的任意取值，另一变量的取值也应服从正态分布
   c. 方差齐性：因变量的总体方差与自变量的方差相同的

4. 方程：
   Y=a+bX
   Y表示因变量的预测值（不是真实值），a表示的y轴的截距，b表示回归方程的斜率，X表示自变量的取值

5. 假设检验：
   在原假设为真（b=0）的情况下，如果检验的结果不可能（p值小于等于0.05），则拒绝原假设，即回归系数不等于0；
   如果检验的结果有可能（p值大于0.05），则接受原假设，即回归系数为0

 

练习：

这是一家超市连续3年的销售数据，包括月份，季度，广告费用，客流量，销售额5个变量，

共36条记录，这里根据广告费用来预测销售额，当广告费用为20万时，销售额大概为多少。
数据：超市销售数据.sav。

 

 

 

 

6. 具体步骤：
   a. 导入数据
   b. 分析数据：分析--回归--线性回归
   c. 解释输出结果：
      描述统计：给出常见统计量
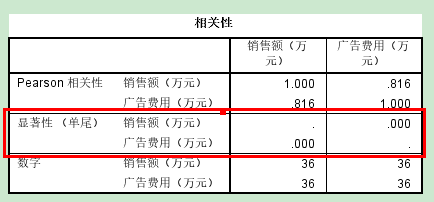
      相关性：两个变量的相关系数，当前的相关系数是0.816，双尾=2*单尾 p值<0.05
                   原假设：H0: ρ=0（不相关）
                   备择假设：H1：ρ≠0（相关）
                   结论：一元线性回归的系数是显著的

       输入/除去的变量：用于预测的自变量（预测变量）

       模型摘要：R（复相关系数）（pearson相关系数） 0~1、R^2、调整后的R^2----因变量能被自变量预测的程度
                       标准估计的误差-------因变量不能被自变量预测的程度
                       R^2用100%相乘得到的结果表示因变量的总方差中能被自变量所解释的比重
                       eg. 广告费用解释了销售额66.6%的方差
                       eg. 用广告费用来预测销售额时，回归方程的平均预测误差就是46.9953
       ANOVA：自变量是否为因变量的显著预测变量
                      p值<0.05, 拒绝原假设，广告费用是销售额的显著预测变量
       系数：构建回归方程+用于检验假设

 

 

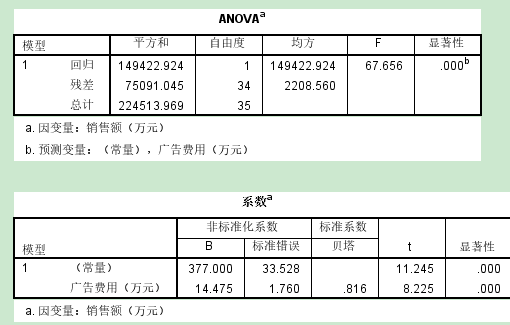
                 Y=a+bX=377+14.475X
                 预测：Y=377+14.475*20=666.50（分析--回归--线性--保存--未标准化）

                 真实值和预测值之间存在差异（R值越大，预测值与真实值越接近）
                 广告费用：p值<0.05, 拒绝原假设，广告费用是销售额的显著预测变量
                 标准化系数：当自变量和因变量都标准化得到的回归系数（在 一元线性回归当中，beta的值等同于皮尔逊相关系数值）

        Y=108.90-0.358*X

 

案例文件

CCSS_Sample.sav，建立用年龄S3来预测总信心指数值的回归方程。

多元线性回归分析

已知两个或多个不同的变量取值，用这些变量来预测另一个变量的值
因变量（标准变量）、自变量（预测变量）
1. 目的：用两个或多个不同的变量取值得到因变量的预测值
2. 所需的数据：
    因变量：连续变量+自变量：连续变量、二分变量
3. 假设条件：
   a. 观测值独立
   b. 总体中变量服从多元正态分布：总体中每个变量的取值服从正态分布，而且每个变量与其他变量的任意组合也服从正态分布（多元正态分布）
  c. 方差齐性：自变量之间的任意组合所形成的总体中因变量的方差都是相同的
4. 多元回归方程：
    Y=β0+β1 X1+β2 X2+…+βnXn
    Y表示因变量的预测值（不是真实值），β0表示的y轴的截距，βn表示回归方程的第n个系数，Xn表示第n个自变量的取值

 

 

5. 原假设和备择假设：
    n个假设检验--检验回归系数（β）
    原假设：H0: “回归系数β1等于0”，即�β1=0
                 H0: “回归系数β2等于0”，即β2=0
                 H0: “回归系数β3等于0”，即�β3=0
    备择假设：H1：“回归系数β1不等于0”，即β1�≠0
                    H1：“回归系数β2不等于0”，即β�2≠0
                    H0: “回归系数β3不等于0”，即β3≠0
    对回归方程正体进行检验，R^2解释因变量的方差
    原假设：H0: R^2=0
    备择假设：H1: R^2>0
6. 假设检验判断：
    在原假设为真的情况下，如果检验的结果不可能（p值小于等于0.05），则拒绝原假设；
                                        如果检验的结果有可能（p值大于0.05），则接受原假设
7. 具体步骤：

 

 

 

 

 

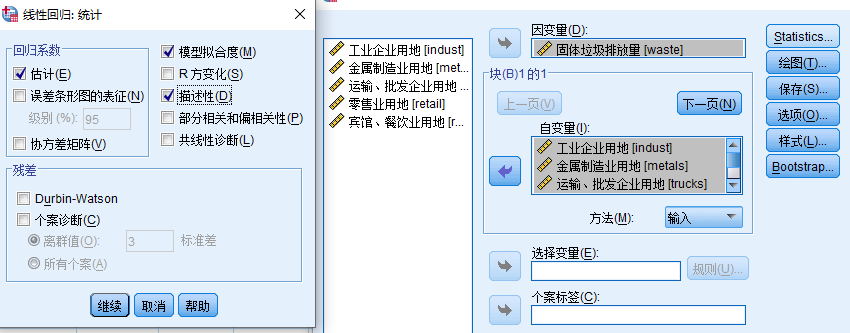
7. 具体步骤：
   a. 导入数据
   b. 分析数据
   c. 解释结果：--【进入法】
      描述统计：统计量
      相关性：相关性越高，预测效果越好

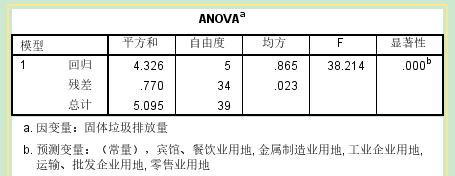
      输入/除去的变量：R--多重相关系数（表示因变量原始数据和回归预测值之间的相关系数的绝对值）
                                 eg. 输入的所有自变量解释了固定垃圾排放量（因变量）84.9%的方差
      ANOVA: ---检验回归的显著性--检验整个方程
                  p值小于0.05，拒绝原假设，接受备择假设，回归方程可以用显著预测出固定垃圾排放量

 

 

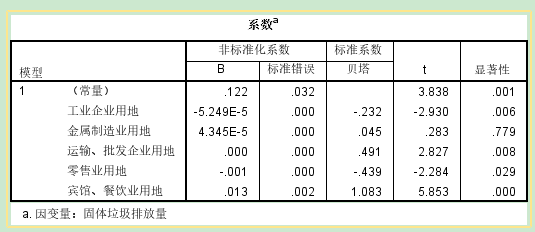
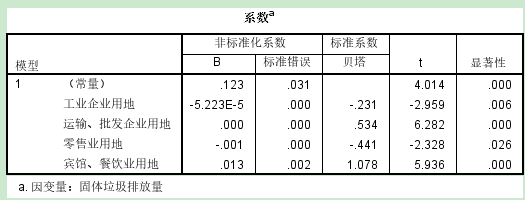
      系数：构建回归方程+检验自变量系数
                alpha=0.05, p值≤0.05，拒绝原假设，该自变量可以预测因变量
                去掉所有不能够预测的自变量，重新构建回归方程

 

 

       解释回归系数：
                 如果回归系数是负值，自变量每增加一个单位，因变量减少对应的系数个单位；
                 如果回归系数是正值，自变量每增加一个单位，因变量增加对应的系数个单位；

       【逐步法】
        自动进行模型的筛选，得到最优模型（R^2最大的模型）

        【自动线性建模】
          通过信息准则（AICC）建模

 

 

11111