杜教筛

BZOJ 3944

题目大意：
求$\sum_{i=1}^{{n}\phi(i)$和$\sum_{i=1}}\mu(i)$
n<2^31

令$F(n)$为$f(n)$前缀和，$G(n)$为$g(n)$前缀和，并且有$g(n)=\sum _{i|n}f(i)$，那么有

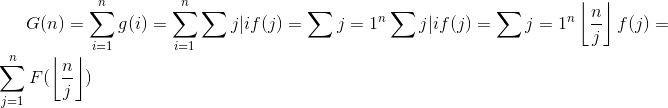
则

$F(n)=G(n)-\sum_{i=2}^{n}F(\left \lfloor {\frac{n}{i}} \right \rfloor)$
n比较小的部分可以用线性筛O(n)搞出来。
n较大的部分用此算法。
复杂度
$O(B+\sum_{i=1}^{\frac{n}{B}}\sqrt{\frac{n}{i}})$
$=O(B+\frac{n}{\sqrt{B}}) $
大约是$B=n^{\frac{2}{3}}$复杂度最小。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int M = 2000000;
int prime[M / 5], tot = 0, n;
ll phi[M + 5], mu[M + 5];
ll p[M + 5], q[M + 5];
bool vis[M + 5];

void init(){
    int i, j;
    phi[1] = mu[1] = 1;
    for(i=2;i<=M;i++){
        if(!phi[i]){
            phi[i] = i - 1;
            mu[i] = -1;
            prime[++tot] = i;
        }
        for(j=1;j<=tot && i*prime[j]<=M;j++)
            if(i % prime[j]){
                phi[i * prime[j]] = phi[i] * (prime[j] - 1);
                mu[i * prime[j]] = -mu[i];
            } else {
                phi[i * prime[j]] = phi[i] * prime[j];
                mu[i * prime[j]] = 0;
                break;
            }
    }
    for(i=2;i<=M;i++){
        phi[i] += phi[i-1];
        mu[i] += mu[i-1]; 
    }
}

ll get_phi(int x){
    return (x<=M)?phi[x]:p[n/x];
}

ll get_mu(int x){
    return (x<=M)?mu[x]:q[n/x];
}

void solve(int x){
    if(x<=M) return;
    int i,j=1,t=n/x;
    if(vis[t]) return;
    vis[t]=1;
    p[t] = ((ll)x + 1) * x >> 1, q[t] = 1;
    while(j < x){
        i = j + 1, j = x / ( x / i), solve(x / i);
        p[t] -= get_phi(x / i) * (j - i + 1);
        q[t] -= get_mu(x / i) * (j - i + 1);
    }
}

int main(){
    int T;
    cin>>T;
    init();
    while(T--){
        scanf("%d",&n);
        memset(vis,0,sizeof vis);
        if(n <= M)
            printf("%lld %lld\n",phi[n],mu[n]);
        else{
            solve(n);
            printf("%lld %lld\n",p[1],q[1]);
        }
    }
    return 0;
}