二分查找

什么是二分查找算法？

二分查找是一种能够将一段区间分为两段，并在此基础上，对需要的区间不断划分、划分...以找到需要的值的查找算法。

复杂度

如果每次判断的点都在区间的中点，时间复杂度为O(lgN)，空间复杂度为O(1)。

使用场景

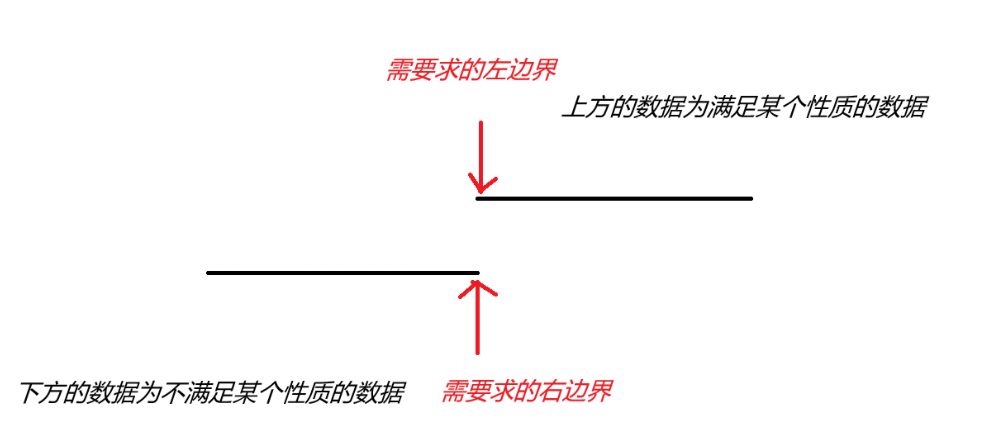
当我们要查找的数据位于一段具有“二段性”的区间的时候，就可以很愉快的使用这种高效算法。什么是具有“二段性”的区间？就是这段区间的左侧或者右侧满足某种性质，而另一侧不具备这种性质（也可以是具备另一种性质）。

升序数组就是一个比较明显的“二段性”区间，当我们需要在这段数组中查找某个值时，数组的左侧小于该值，而右侧大于该值。

算法的坑点

我们在写二分查找算法的时候，mid的取法、循环条件以及left和right的取法都可能成为程序运行超时的罪魁祸首。

算法模板

1、朴素的二分模板
https://leetcode.cn/problems/binary-search/description/
这道题是朴素二分的模板题

2、求左边界的二分模板
3、求右边界的二分模板
https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/
这道题是求左边界和右边界的模板题

朴素的二分模板

当我们需要查找某个值的时候，我们就可以使用朴素二分。以下是模板：

点击查看代码

while(left<=right)
{
	int mid = left+(right-left+1)/2;
	// 也可以写成 int mid = left+(right-left)/2;
	if(...)
		left = mid+1;
	else if(...)
		right = mid-1;
	else
		return ......;
}

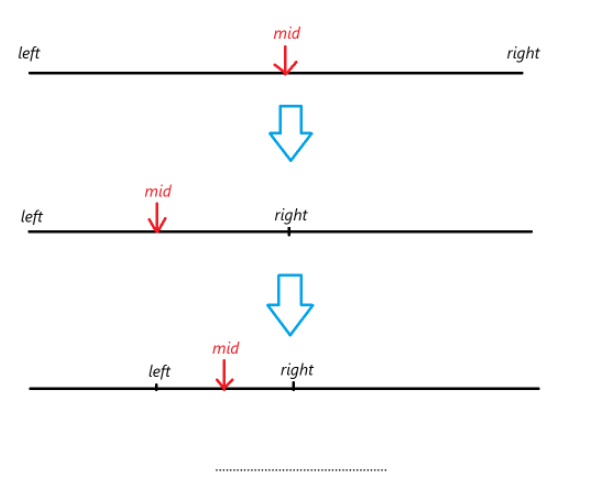
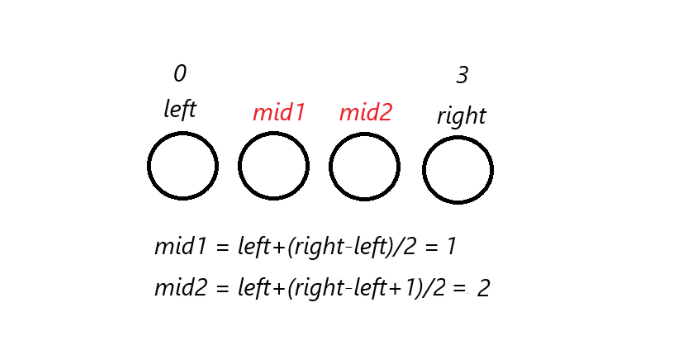
此时while的循环条件为left<=right，left==right时需要走一次判断。图中mid的写法是为了防溢出。在朴素二分的情况下，+1与否没什么影响。+1与否的区别在于，当区间内数的数量为偶数时，+1的mid指向中间偏右的数，没有+1的mid指向中间的偏左的数，而数量为奇数时无区别。例如：

求边界的二分模板

左边界

以下是模板：

点击查看代码

while(left<right)
{
	int mid = left+(right-left)/2;
	if(...)
 		left = mid+1;
	else
		right = mid;
}

在寻找左边界的过程，我们希望让left<right，并在left==right时找到左边界，所以我们这里将right赋值为mid，将left赋值为mid+1，让left逐渐靠近right。这里我们的mid并未+1，在最后剩下两个数据时，我们期望让mid指向左边的数，这样无left和right的下一次更新都会使循环结束。如果mid指向右边，在满足right更新的情况下，right不会改变，也就陷入了死循环。

右边界

以下的模板：

点击查看代码

while(left<right)
{
	int mid = left+(right-left+1)/2;
	if(...)
		left = mid;
	else
		right = mid-1;
}

寻找右边界的想法与左边界相反，这里不再赘述。

以上就是二分查找算法的模板以及注意点。（勿喷QAQ）