树

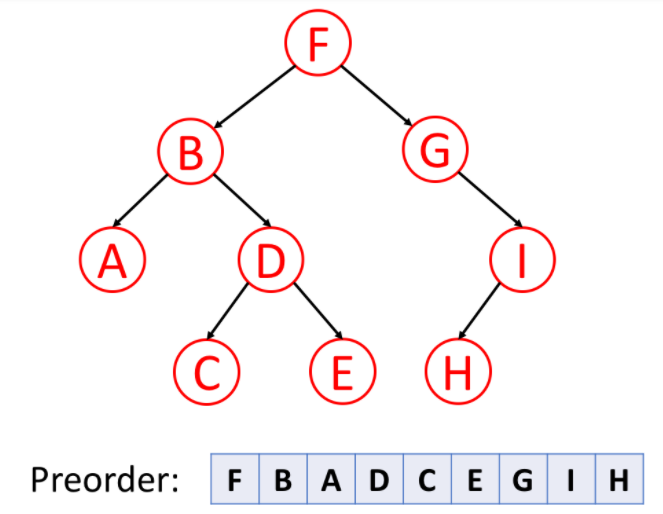
（1）前序遍历：前序遍历首先访问根节点，然后遍历左子树，最后遍历右子树

 

 

 

 （2）中序遍历：中序遍历是先遍历左子树，然后访问根节点，然后遍历右子树

 

 

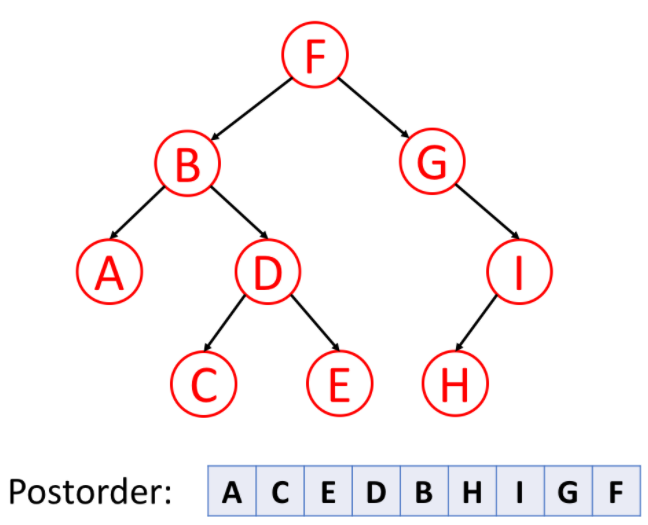
 （3）后序遍历：后序遍历是先遍历左子树，然后遍历右子树，最后访问树的根节点。

 

 

 二  树的存储结构

public class TreeNode {
  int val;
  TreeNode left;
  TreeNode right;

  TreeNode(int x) {
    val = x;
  }
}

三 迭代（栈）

从根节点开始，每次迭代弹出当前栈顶元素，并将其孩子节点压入栈中，先压右孩子再压左孩子。

在这个算法中，输出到最终结果的顺序按照 Top->Bottom 和 Left->Right，符合前序遍历的顺序。

//  前序遍历

class Solution {
  public List<Integer> preorderTraversal(TreeNode root) {
    LinkedList<TreeNode> stack = new LinkedList<>();
    LinkedList<Integer> output = new LinkedList<>();
    if (root == null) {
      return output;
    }

    stack.add(root);
    while (!stack.isEmpty()) {
      TreeNode node = stack.pollLast();   // 取最后一个，然后删除
      output.add(node.val);
      if (node.right != null) {
        stack.add(node.right);
      }
      if (node.left != null) {
        stack.add(node.left);
      }
    }
    return output;
  }
}

 四 递归

//前序遍历

public static void PreOrderRecur(TreeNode<char> treeNode)
 {
     if (treeNode == null)
     {
         return;
     }
     Console.Write(treeNode.Data); 
     PreOrderRecur(treeNode.LChild);
     PreOrderRecur(treeNode.RChild);
 }

//中序遍历

public static void InOrderRecur(TreeNode<char> treeNode)
{
    if (treeNode == null)
    {
        return;
    }  
    InOrderRecur(treeNode.LChild);
    Console.Write(treeNode.Data); 
    InOrderRecur(treeNode.RChild);
}

//后序遍历
public static void PosOrderRecur(TreeNode<char> treeNode)
{
    if (treeNode == null)
    {
        return;
    }
    PosOrderRecur(treeNode.LChild);
    PosOrderRecur(treeNode.RChild);
    Console.Write(treeNode.Data); 
}

 

// 中序遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        inorder(root, res);
        return res;
    }

    public void inorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        inorder(root.left, res);
        res.add(root.val);
        inorder(root.right, res);
    }
}

 利用递归，给定一个二叉树，找出其最大深度

class Solution {
    public int maxDepth(TreeNode root) {
    if(root==null){
        return 0;
    }
    return 1+Math.max(maxDepth(root.right),maxDepth(root.left));
    }
}

 

 

 

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);
    }
}