LUA: 使用递归和尾调用优化代码

LUA: 使用递归和尾调用优化代码

为方便阅读，先上结论：可以优化，但没必要； 这篇文章基于以下前提：

1. 使用递归+尾调用优化可以在不影响程序效率的前提下，改善代码结构，体高代码可读性
2. 当前函数栈的无需要保留的信息，才会发生尾调用

一个对象转字符串的例子

考虑将下面的一个容纳了多个table的数组快速拼接成一个长字符串

local list = {}
local mt = { __tostring = function(v) return tostring(v.value) end}
-- 初始化
for i = 1, math.random(8, 10) do
    table.insert(list, setmetatable({
                remove = false,
                value = i
            }, mt))
end

for循环实现

table.concat 只接受元素类型为string或number的数组，不会为非上述类型的元素调用tostring，上面元事件__tostring不会被触发，所以需要创建一个字符串数组，每一个元素为前述数组元素的tostring调用返回值； 下面是最基础的实现方式：

local function genfor(t)
    local b = {}
    for i, v in ipairs(t) do
        table.insert(b, tostring(v))
    end
    return b
end
print(table.concat(genfor(list), ","))

看着还行， 但是表的初始化可以一步完成吗？先指定数组容量，可以避免数组在扩展时候的内存重新分配。除了C API 中的void lua_createtable (lua_State *L, int narray, int nrec)函数，初始化指定容量只有标量表达式（如： t = {1,2,3,4,}） ，以及使用变长参数来构造表（如：local t = {...}）。

递归实现

也就是说，只要有一个函数，类似于table.unpack，可以将数组中每一元素执行tostring之后再返回所有内容，就可以在确定数组长度时候构造table；下面是一个使用递归实现的例子：

local function genrecur(t, i)
    if not i then
        -- 递归的最外层，此处接受N个返回值，并构造了表
        return {genrecur(t, 1)}
    end
    if i > #list then
        -- 递归的终止条件
        return
    end
    -- 递归的状态转移， genrecur(i) = list[i], genrecur(i)
    return tostring(t[i]), genrecur(t, i + 1)
end
print(table.concat(genrecur(list), ","))

也还行， 看着还很厉害，测试下性能：

local function cost(f, ...)
    local a = os.clock()
    f(...)
    return os.clock() - a
end

local function testwithN(N)
    local list = {}
    for i = 1, N do
        table.insert(list, setmetatable({
                    remove = false,
                    value = i
                }, mt))
    end
    local a = cost(genfor, list)
    local b = cost(genrecur, list)
    print(("%6d: %.2f"):format(N, b/a))
end
print(("%6s: %s"):format("size", "recur/forloop"))
for __, n in ipairs({0, 4, 8, 64, 128, 1024, 4096, 8192}) do
    testwithN(n)cost
end

测试结果：

  size: recur/forloop
     0: 1.50
     4: 0.54
     8: 1.27
    64: 1.42
   128: 1.04
  1024: 1.69
  4096: 1.86
  8192: 4.67

尾调用递归实现

当表的长度越来越大的时候，递归的效率就较for循环越发低下， 考虑原因，是随着数组长度增加，递归的层数也单调增加了；再试试使用尾调用的递归实现：

local function genrecurx(t, i, ...)
    if not i then
        -- 递归的最外层，提供初始化参数
        return genrecurx(t, #t) 
    end
    if i < 1 then
        -- 递归的终止条件，将变长参数打包成表
        return {...}
    end
    -- 递归的状态转移， genrecurx(n - 1, ...) = genrecurx(n - 1, t[n], ...)
    return genrecurx(t, i - 1, tostring(t[i]), ...)
end 

这里使用了一个技巧，将表内容解出压在了变长参数列表头部， 避免递归函数栈中存有保留信息，进而可以享受到lua的尾调用优化；这样，无论数组有多长，递归的堆栈都只有一层；测试一下性能如何：

  size: recur/forloop recurx/forloop
     0: 0.50 0.50
     4: 0.59 0.50
     8: 0.78 0.74
    64: 1.19 0.80
   128: 1.09 1.07
  1024: 1.64 1.61
  4096: 1.92 1.81
  8192: 5.94 10.44

晴天霹雳，使用了尾调用，效率反而比有常规递归实现还要差！

分析原因，发现上面递归代码中，虽然旧的函数栈已经清空，但是每次插入新元素到变长参数列表中，都会将变长参数所有元素后移一位！ 见下图：

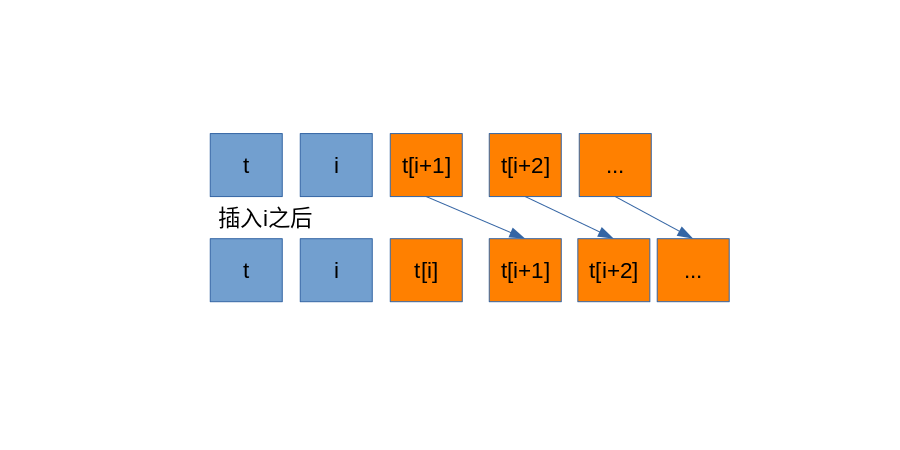
而常规递归实现效率更高的原因在于，每次添加元素，新元素是插入到之前栈尾部的，没有移位操作；见下图：

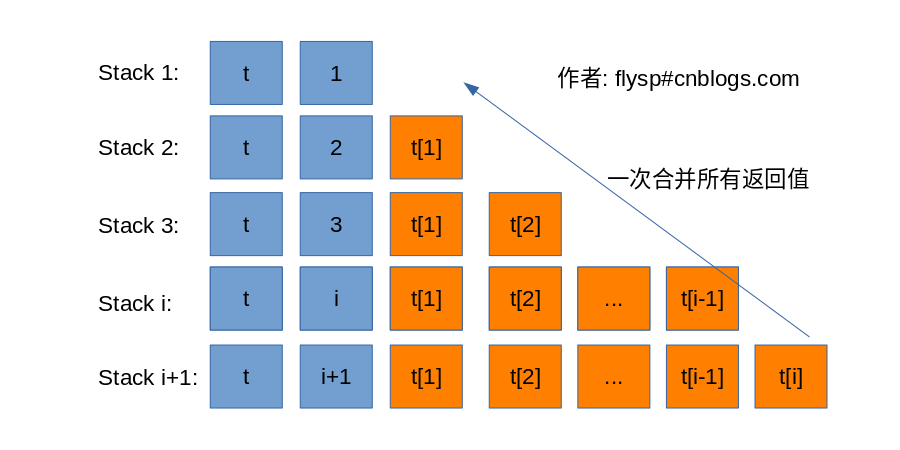
虽然常规递归会展开N个函数栈，但是在到达最后一个元素时候，所有的函数栈收缩，依次合并所有的返回值，反而效率比尾调用优化实现要高；当然函数栈也是占有了临时空间的。

最终实现

折腾了那么多，所谓代码结构优化，反而拖累了运行效率，那么最终的可用的代码结构是怎样的呢？如下：

local function genrecurt(t, r, i)
    if not r then
        -- 递归最外层，分配结果表，和起始下标
        return genrecurt(t, {}, 1)
    end
    if i > #t then
        -- 递归终止条件，返回结果表
        return r
    end
    -- 递归状态转移， genrecurt(t, r, i)  = genrecurt(t, {r[:#r], t[i]}, i+1)
    table.insert(r, tostring(t[i]))
    return genrecurt(t, r, i + 1)
end 

性能测试：

  size: recur/forloop recurx/forloop recurt/forloop
     0: 0.67 0.56 0.56
     4: 0.90 0.57 0.62
     8: 1.45 0.82 0.95
    64: 1.01 0.52 0.57
   128: 1.07 1.00 0.95
  1024: 1.54 1.83 0.91
  4096: 1.87 1.95 0.24
  8192: 5.64 10.06 0.95

可以明显看到，最终实现的性能非常稳定，不会因数组长度增加而急剧地碰撞；而且让我挺惊讶的是，这个实现居然比for循环还快（虽然差异不高，基本持平）。

结论

综合看下来，还是for循环最好， 性能不差，而且直观——最笨往往是最好的；但是递归和尾调用，在拆解比较复杂的逻辑的场景，能在不影响效率的前提下，很大程度抽象出代码逻辑（比如迭代器）；希望这篇文章可以给您带来这方面的启发