Dijkstra算法（内附c++代码）

Dijkstra是一种经典且高效的单源最短路径算法，其本质是一种贪心算法，通过对图向外层层扩展得到从某一给定点到所有其它点的最短路。

操作步骤

1. 记已找到最短路的点为集合S，未找到的点为集合Q，显然初始状态为除起点外的点都在集合Q中。
2. 将起点加入集合S中，同时更新集合Q中的点与起点的距离，与起点直接相连的点距离为边权，不直接相连的点距离为正无穷，记dis[i]为i点与起点的距离。
3. 将集合Q中dis[]最小的点x取出，加入S集合，遍历与x相邻的点（将这些点记为y），更新这些点与起点的距离，dis[y]=min{dis[y],dis[x]+边权[x][y]}（这一步即为对Q集合的更新） 。这一步是dijkstra的精髓
4. 重复进行步骤3，直到所有点都已加入S集合。

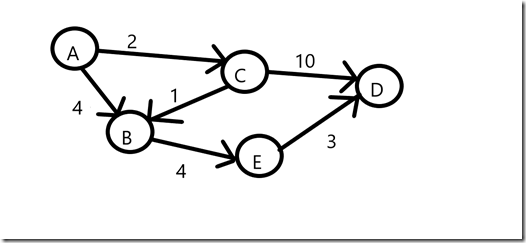
图解(电脑自带的画图画的，就这样吧。。)

我们以A为起点，模拟一下整个算法的流程。
1. 将A点加入集合S，同时更新与A点直接相连的B，C距离，dis[B]=4,dis[C]=2,此时dis[D]=正无穷，dis[E]=正无穷。
2. 将dis最小的C点取出，加入集合S，同时更新与C点相邻的点的距离，dis[D]=12,由于dis[C]+边权[C][D]<dis[B],所以dis[B]=3。
3. 同上，此时dis最小的为B取出加入集合S，dis[E]=7。
4. 现在dis最小的为E，同上，dis[D]=10。
5. 现在dis最小的为D，此时所有点都已进入集合S，程序结束。

但dijkstra算法是有局限的，它只能用来处理边权全部为正的图，不能处理有负权边的图，因为这种情况下当一个点加入集合S后该点仍有可能通过负权边来缩小dis。

以下为代码

#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
struct stu{
    int to,next;
    long long int cap;//前向星存图，以一点为起点，to为该边连接的一个点，next为与该边起点相同的下一条边，cap为边权
};
stu road[2000050];
int head[2000050],k=0,vis[1000050];//vis为集合S 
int n,m,s;
long long int dis[1000050];
struct node
{
    int u;
    long long d;
    bool operator<(const node& rhs)
    const
    {
        return d>rhs.d;
    }
};
priority_queue<node>q;//用优先队列来实现取出集合Q中dis最小值的点的功能 
void add(int x,int y,long long int z) 
{
    road[k].to=y;
    road[k].next=head[x];
    road[k].cap=z;
    head[x]=k;
    k++;
}
void dijkstra(int x)
{
    for (int i=1;i<=n;i++)
    {
        dis[i]=2147483647; //开始所有点都没有遍历过，所以所有点与起点的距离初值为正无穷
    }
    q.push((node){s,dis[s]});
    dis[x]=0;
    while(q.empty()==0)
    {
        node uu=q.top();
        int u=uu.u;
        q.pop();
        if (vis[u]==1)
        {
            continue; 
        }
        vis[u]=1;//将当前点加入集合S 
        for (int i=head[u];i>-1;i=road[i].next)
        {
            int v=road[i].to;
            if (dis[v]>dis[u]+road[i].cap)//更新dis 
            {
                dis[v]=dis[u]+road[i].cap;
                q.push((node){v,dis[v]});
            }
        }
    }
}
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d%d",&n,&m,&s);
    for (int i=1;i<=m;i++)
    {
        int a,b;
        long long int c;
        scanf("%d%d%lld",&a,&b,&c);
        add(a,b,c);
    }
    dijkstra(s);
    for (int i=1;i<=n;i++)
    {
        printf("%lld ",dis[i]);
    }
    return 0;
}