BUAA-OO-Unit3 总结

BUAA-OO-Unit3 总结

(0) 写在前面

关于JML

围绕着本单元的一个核心的话题就是JML语言的大致理解，我觉得JML语言的要点是提出需求的一方和编写程序的一方之间达成的约定，而这种约定相比于自然语言，很少出现二义性，因此通过JML语言，课程组可以非常方便清晰地向我们传达作业的需求。

但是JML语言有一个缺点就是相比于自然语言又太过于复杂，想要写好JML语言描述，也需要花上功夫，这可能也是本单元训练的一个重点和难点吧，就是希望能够训练同学们用形式化语言将程序结构设计规格化。

想要读懂JML语言，大致需要知道的就是下面几点：

• requires 子句定义该方法的前置条件
• assignable副作用范围限定， 列出这个方法能够修改的类成员属性，\nothing 是个关键词，表示这个方法不对任何成员属性进行修改
• ensures 子句定义了后置条件
• signal子句会定义在何种条件之下抛出何种异常

在编写代码时，我习惯先编写带有/*@ pure @*/的方法，因为它们非常简单；在编写较为复杂的方法时，我会首先关心exceptional_behavior，把所有可能的该抛出的异常放在前面写完，然后再去关心normal_behavior的具体实现逻辑。

还有一点是，JML语言实质上只是描述了功能，但是具体实现的时候，还是应当结合具体情况，进行算法优化、结果缓存等优化策略，否则程序的效率难以保证。我在编码时会首先严格按照JML语言实现一个版本，然后经测试无误即表明自己对JML语言的理解没有问题，然后在其基础上着手进行算法上的优化。

(1) 如何利用JML规格来准备测试数据

准备测试数据时，分成两个方面即白盒测试和黑盒测试两类准备测试数据

白盒测试

• 在测试过程中需要我们针对JML的条件来构造测试数据，即针对JML中的每一个ensure或是request来设置对应的测试点
• 还需要尤其注意异常行为中抛出异常的顺序、抛出异常的参数是否正确，这也需要我们覆盖到
• 同时我们可能写了一些数据结构比如并查集、图、元组等，维护图中的数据，优化我们的算法，因此在进行单元测试时，需要着重对这些数据结构进行单独的测试，不仅要测试是否正确，也要测试是否如我们所愿优化了我们程序的运行速度
• 在测试过程中结合Junit工具可以对程序的每一个分支都进行充分的测试
• 总之要做到对JML中的条件应测尽测，只有确保函数所有的行为都符合规格才可认为是完全正确的

黑盒测试

• 我们的做法就是用暴力的方法随机生成大量的样例进行对拍测试，一定要多找几个人对拍，因为两个人可能都没有认真看JML（最典型的问题就是在计算年龄方差时的精度问题，甚至一个宿舍四个人可以同时出现错误）
• 随机生成的数据大部分都是无效数据，因此虽说是随机生成数据测试，但是也要有一定章法
• 加人时，随机生成一个PersonId范围\(p\)，之后每一条ap指令都只能从\([0, p)\)内随机取值，其他涉及到PersonId的指令将会从\([0, p+10)\)内随机取值以保证能够触发PersonIdNotFoundException，用这种技巧保证既不会测试时抛出大量异常，同时也会测出异常
• 测试最短路、最小生成树时，先生成随机图，然后再进行其他指令的随机生成；随机图会生成若干类，可以是点数很少的图，也可以是是非常庞大的图，还可以生成链等，然后合并生成的多张随机图，这样保证了数据多样性

(2) 梳理架构设计，分析图模型构建和维护策略

首先按照惯例放出类图，因为作业是迭代的，因此只放出第十三次作业的类图

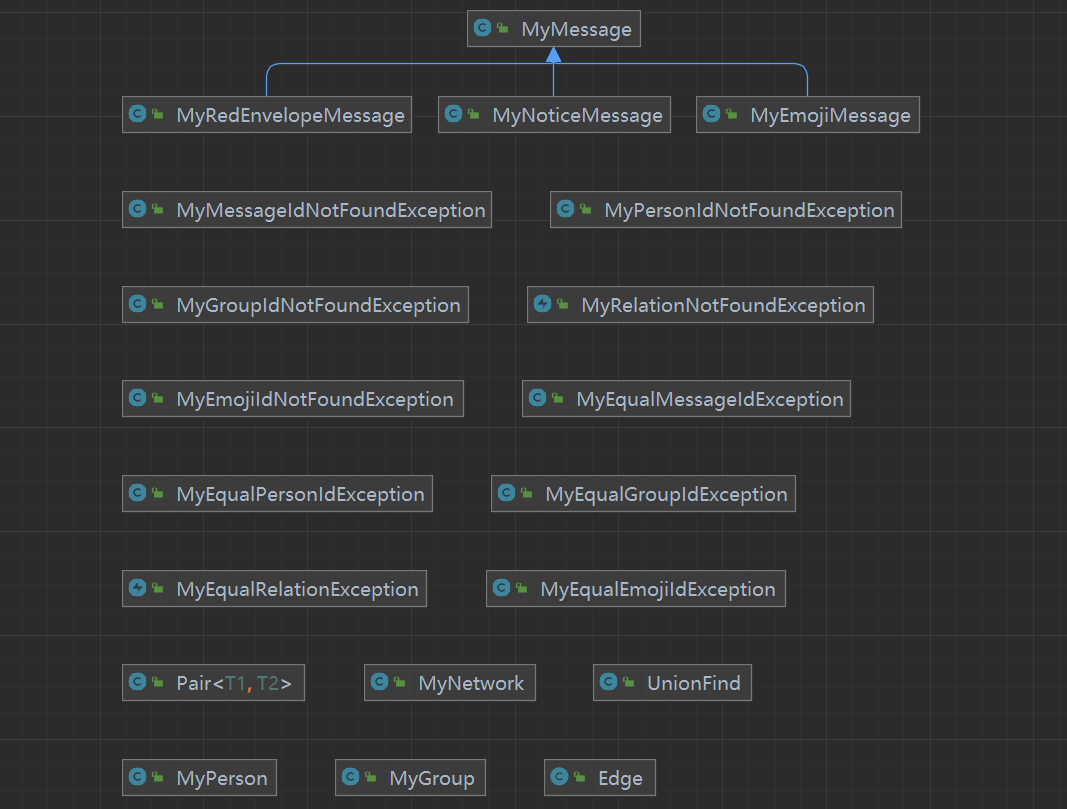
事实上，我们的设计架构是JML语言所约定好的，因此类图必然也都是大同小异的，换言之，如果类图实现的与标准不同，那反而应该是一份错误的没有实现JML规格的代码。

图的模型构建

事实上我们的确不太需要考虑图是如何构建的，节点和边是如何加入的，因为这一切都是TA们在JML语言里面帮我们完成的，后来稍微思考一下不难发现，其实我们的图就是一个Network，图中的节点是Person，图中的边是Relation，这一切隐含在了Person类中的Association这个数组中了，实际上应该是一个邻接表的结构，了解了这一点后，我们可以利用数据结构的相关知识实现图论算法，优化复杂度

数据维护策略

• 考虑到各个对象都有一个唯一的id，而且需要根据id进行各种查找，所以我们没有理由不去使用HashMap去保存各类对象
• 对于不会重复的元素，实测的结果是使用HashSet会比ArrayList要快许多
• 然后Message需要添加在头部，所以很明显提示我们用LinkedList保存Message
• 在编写最小生成树和最短路时，用优先队列PriorityQueue可以提高效率
• 同时Java没有原生的元组，所以我自己用泛型实现了一个Pair<T1, T2>

(3) 分析代码实现出现的性能问题和修复情况

这个部分也是本次作业需要着重注意的地方，按照往届同学的说法，算法的复杂度不能高于\(O(n^2)\)，下面简要介绍一下我的实现

连通性判断、连通块计数的算法——并查集

• 这个算法被用来实现isCircle方法和 queryBlockSum方法

• 由于直接深度搜索的效率太低，应该是\(O(n^2)\)的复杂度，所以采用了并查集算法进行性能优化

• 为了防止并查集的树退化，还进行了合并操作，每一次有新的连接被建立，就将较小的树加到较大的树上去（按秩合并）

• 每一次搜索时，都把叶子节点直接连接到根节点上（路径压缩）

• 优化过后的算法可以将查找时复杂度降为\(O(1)\)

• 连通块计数相当于在问并查集中有几棵树，最开始的做法是通过遍历并查集所有元素，当其父亲为自身时，代表其是一个连通块的代表元（根节点），复杂度\(O(n)\)

• 但是我们可以直接维护blockSum属性用于统计连通块数量，并在在addPerson和addRelation时更新其值，算法复杂度降为\(O(1)\)

最小生成树——Kruscal算法

• 这个算法被用来实现queryLeastConnection

• 使用Kruskal算法，然后把连接性判断的算法用并查集维护一下就行，比较简单

• 不建议使用Prim，实测速度不如Kruscal

• 算上排序复杂度因该是\(O(nlogn + n)\)，可以直接使用优先队列加边

• 后来我们发现我们的操作中是没有删边的，那么我们可以动态维护最小生成树的结果

  • 考虑如果在两个不连通的块之间添加一条边，那么新的最小生成树就是原本两边的和加上新的边权
  • 如果在连通块内添加一条边，则需要重新计算最小生成树
  • 因此可以考虑对结果进行缓存

  // 并查集的merge方法
  int faID1 = getFather(id1);
  int faID2 = getFather(id2);
  if (faID1 == faID2) {
      this.mstCached.put(faID1, -1);
  } else {
      if (rank.get(faID1) <= rank.get(faID2)) {
          fa.put(faID1, faID2);
          // blocks.get(faID2).addAll(blocks.get(faID1));
          // blocks.remove(faID1);
          if (mstCached.get(faID1) != -1 && mstCached.get(faID2) != -1) {
              mstCached.merge(faID2, mstCached.get(faID1) + value, Integer::sum);
          } else {
              mstCached.put(faID2, -1);
          }
      } else {
          fa.put(faID2, faID1);
          // blocks.get(faID2).addAll(blocks.get(faID1));
          // blocks.remove(faID1);
          if (mstCached.get(faID1) != -1 && mstCached.get(faID2) != -1) {
              mstCached.merge(faID1, mstCached.get(faID2) + value, Integer::sum);
          } else {
              mstCached.put(faID1, -1);
          }
      }
      if (rank.get(faID1).equals(rank.get(faID2))) {
          rank.merge(faID2, 1, Integer::sum);
      }
      blockSum--;
  }
  

  // queryLeastConnection的部分代码
  // MST (Cached)
  if (relation.getMstCached(id) != -1) {
  	return relation.getMstCached(id);
  }
  
  mstUF = new UnionFind();
  PriorityQueue<Edge> edges = new PriorityQueue<>();
  dfsAndAddEdge(edges, getPerson(id));
  
  int tot = 0;
  int sum = 0;
  while (!edges.isEmpty() && tot != mstUF.size() - 1) {
      Edge edge = edges.poll();
      assert edge != null;
      if (!mstUF.inSameBlock(edge.getSrc(), edge.getDst())) {
          mstUF.merge(edge.getSrc(), edge.getDst(), 0);
          tot++;
          sum += edge.getWeight();
      }
  }
  relation.setMstCached(id, sum);
  return sum;
  

最短路径——Dijkstra算法

• 这个算法被用来实现sendIndirectMessage
• 用经过堆优化的Dijkstra算法
• 算法复杂度应该是\(O(nlogn)\)

一些奇技淫巧

• 我们考虑对所有耗时的操作进行缓存，当计算得到的数值可以重复使用时，我们用一个HashMap把询问和答案存起来，如果下次询问前这部分没有变化，那么我们直接返回缓存的值
• 年龄和、年龄方差等信息要动态维护，否则是有被卡的可能性的，在第十次作业中，利用这一点我在互测房间中完成五杀
• 不知道为什么原因Java中的String.format方法要远远慢于直接System.out.print，考虑到运行效率，并不建议使用format

Bug修复的分析

在互测中被发现一个bug

Bug	所在类	所在方法	原因
java.lang.StackOverflowError	MyNetwork	dfsAndAddEdge	不明

这是让我非常困惑的一个bug，按理来说hack我的数据应当不会让我爆栈才对

最后查明问题在于使用了lamda表达式，稍作修改把lamda表达式替换成for循环即可解决问题

总之是非常奇怪的一个bug

(4) 针对下面内容对Network进行扩展，并给出相应的JML规格

假设出现了几种不同的Person

• Advertiser：持续向外发送产品广告
• Producer：产品生产商，通过Advertiser来销售产品
• Customer：消费者，会关注广告并选择和自己偏好匹配的产品来购买 -- 所谓购买，就是直接通过Advertiser给相应Producer发一个购买消息
• Person：吃瓜群众，不发广告，不买东西，不卖东西

如此Network可以支持市场营销，并能查询某种商品的销售额和销售路径等 请讨论如何对Network扩展，给出相关接口方法，并选择3个核心业务功能的接口方法撰写JML规格（借鉴所总结的JML规格模式）

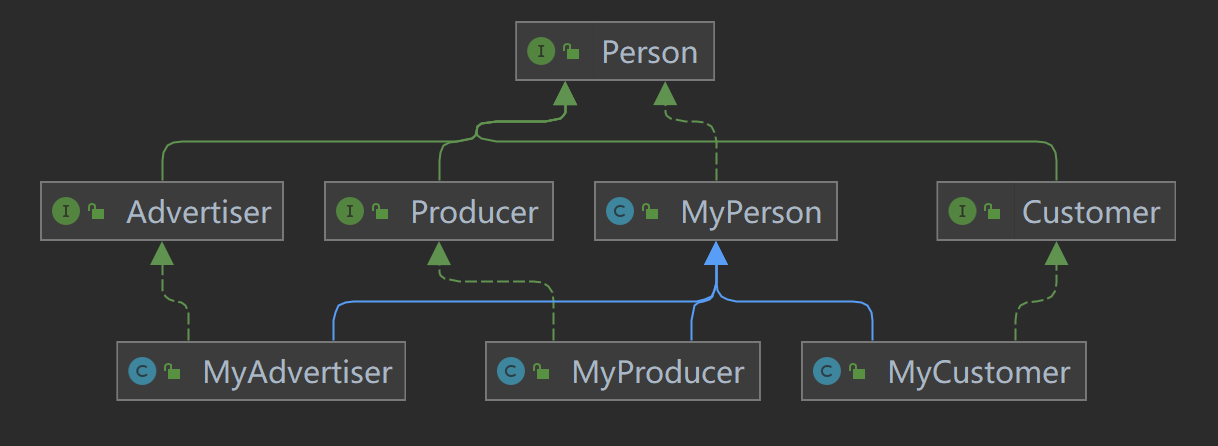
把扩展的类和接口简单的用IDEA模拟一下实现和继承关系，可以画出如上图所示的类图

我们可以新建三个类实现Person接口，以此来管理Advertiser、Producer以及Customer。新建两个类实现Message接口，以此来管理SendProductMessage、PurchaseMessage和AdvertiseMessage的有关信息

在这种情形下，NetWork需要新设立以下的方法：添加一个商品的addProduct方法，生产商发送产品信息广告给Advertiser的sendAdvertiseMessage方法，顾客购买产品即purchaseProduct方法，顾客查询Advertiser的广告信息确定是否有自己需要的产品getAdvertisement，同时为了查询有关产品的销售额以及销售路径，可以新建其它查询查询方法。

下面选取三个方法编写JML规格

添加新的产品

这时Message接口需要被一个新的AdvertiseMessage实现

/*@ public normal_behavior
  @ requires !(\exists int i; 0 <= i && i < messages.length; messages[i].equals(message)) &&
  @ message.getType() == 2 && (message.getPerson1() instanceof Advertiser);
  @ assignable messages;
  @ ensures messages.length == \old(messages.length) + 1;
  @ ensures (\exists int i; 0 <= i && i < messages.length; messages[i].equals(message));
  @ ensures (\forall int i; 0 <= i && i < \old(messages.length);
  @         (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i]))));
  @ also
  @ public exceptional_behavior
  @ signals (EqualMessageIdException e) 
  @         (\exists int i; 0 <= i && i < messages.length; messages[i].equals(message));
  @ signals (AdvertiserNotFoundException e) 
  @         !(\exists int i; 0 <= i && i < messages.length; messages[i].equals(message)) 
  @           && !(messages[i].getPerson1() instanceof Advertiser);
  @*/
public void addAdvertiseMessage(Message message) throws EqualMessageIdException, AdvertiserNotFoundException;

查询消费者购买的产品数量

/*@ public normal_behavior
  @ requires (\exists int i; 0 <= i && i <= people.size; 
  @                     people[i].equals(producer) && people[i] instanceof Customer)
  @ ensures (\exists int i; 0 <= i && i <= people.size; 
  @                     people[i].equals(producer) && people[i] instanceof Customer && 
  @						\result == people[i].getProductCount)
  @ also
  @ public exceptional_behavior
  @ signals (PersonIdNotFoundException e) 
  @           (\forall i; 0 <= i && i < people.size; !people[i].equals(producer))
  @*/
public int queryCustomerProductCount(Person consumer) throws PersonIdNotFoundException;

添加商品

/*@ public normal_behavior
  @ requires (\exists int i; 0 <= i && i < people.length;    
  @          people[i].getId() == id && people[i] instanceof Producer); 
  @ assignable product;
  @ assignable getProducer(id).product;
  @ ensures product.length == \old(product.length) + 1;
  @ ensures (\forall int i; 0 <= i && i < \old(product.length);
  @         (\exists int j; 0 <= j && j < product.length; product[j] ==   
  @         (\old(product[i]))));
  @ ensures (\exists int i; 0 <= i && i < product.length; product[i] ==   
  @		     product);
  @ ensures getProducer(id).product.length ==    
  @          \old(getProducer(id).product.length) + 1;
  @ ensures (\forall int i; 0 <= i && i < \old(getProducer(id).product.length);
  @         (\exists int j; 0 <= j && j <getProducer(id).product.length;   
  @       getProducer(id).product[j] == (\old(getProducer(id).product[i])));       
  @ ensures (\exists int i; 0 <= i && i < getProducer(id).product.length;   
  @          getProducer(id).product[i] == product);
  @ also
  @ public exceptional_behavior
  @ signals (PersonIdNotFoundException e) 
  @         (\forall i; 0 <= i && i < people.size; !people[i].equals(producer))
  @*/
public void addProduct(Product product, int id);

(5) 本单元学习体会

• 本单元作业的大部分要求都是通过JML规格体现的，因此首先需要结合理论课讲授的知识深入理解JML，包括但不限于相关语法、特性、注意事项等；
• JML语言个人觉得太过于繁琐，之后可能不会再使用了，但是这种通过规格约束去规范软件开发、避免出现需求传达的二义性的做法，我认为是非常值得学习的，比如说求最小生成树，对于学习过数据结构的同学，直接说明最小生成树五个字有可能比正确、严谨的书写出JML语言描述更加容易且不会出错，这对JML语言的编写者也提出了不小的挑战；
• 阅读JML并不轻松，需要注意其中的每一句话，不能忽略每一个条件（当然实际操作中，我会直接把条件复制到代码中避免出错）。尤其是一些细节，一旦理解出现偏差很有可能导致大bug的出现（比如说年龄方差的计算，就需要严格按照JML来写，即使整数运算存在误差）。此外，对于一些复杂的方法，JML语言与自然语言会有很大的差别，例如最小生成树和最短路算法的表述就非常反人类，很难在第一时间明白我们需要做什么，这就要求读者拥有一定的耐心和逻辑推理能力；
• 善于运用lamda表达式和Java的stream可以大大的简化代码（虽然也出现了一些未知的问题）
• 事实上，JML语言应当属于是契约式编程的一种，契约式编程的主要目的是希望程序员能够在设计程序时明确地规定一个模块单元（具体到面向对象，就是一个类的实例）在调用某个操作前后应当属于何种状态，它更像是一种设计风格或一种语法规范，这是不是与JML语言中的ensures和requires极为类似？
• 契约式编程确实有助于开发效率的提升，让每个人都对自己写的代码负责，在开发者之间建立良好的信任关系，同时也能减少不必要的沟通成本和精力，以及本可通过协商避免的相互提防，跟现在的UML单元比较，UML单元采用自然语言表述，就有很大的二义性，在讨论区和微信群中就会有同学不断提问，JML语言描述就不会出现这种情况。