题解：CF1399E1 Weights Division (easy version)

题目链接

很有意思的一道题，题解里面大部分都是链式前向星来存且年代久远，这里写一篇 vector 的。

分析

题目的要求很简单，选取一条边使其权值 \(w\) 变为 \(\left \lfloor \frac{w}{2} \right \rfloor\)，最终使根节点到所有叶子结点的路径之和不大于 \(S\)。

解法

观察到可以将所有边的权值 \(\times\) 该边的使用次数来进行比较，判断优先级。
简单举个例子理解一下，如下图。

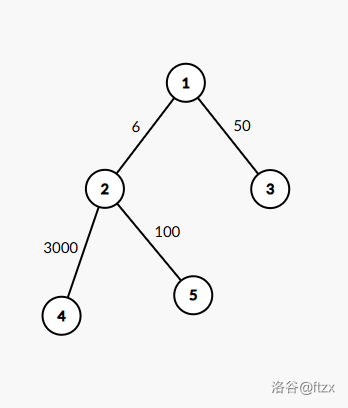
假如我要把数字控制在 \(2999\) 内，观察到 \(6 \times 2 < 3000 \times 1\)。
对 \((2,4)\) 两条边进行处理明显比处理 \(4,5\) 的公共父边 \((1,2)\) 更优。（毕竟 \(6\) 再怎么删也到不了负数）。

那么按照我们的策略，就可以轻松完成这道题了
（具体见下面优先队列）。

处理

既然要统计每条边的使用次数，那 dfs 一遍即可。
此时我们可以对每对点（每条边）映射一个值 \(i\) （在读入时处理）。
定义 \(f[i]\) 表示第 \(i\) 条边的使用次数。
dfs 如下。

void dfs(int u,int fa){
	bool flag=0;
	for(int i=0;i<g[u].size();i++){
		int v=g[u][i];
		if(v!=fa){
			dfs(v,u);
			f[G[u][v]]=dp[v];
			dp[u]+=dp[v];
			flag=1;
		}
	}
	if(!flag){
		dp[u]=1;
	}
}

接下来就是要初始化所有的边权 \(\times\) 次数，这时可以使用优先队列处理。同时把现在的路径之和 \(sum\) 求出来。

这里来解释一下排序策略，要让一个贡献更大的排在前面。
这里的贡献就是在边权除二后使 \(sum\) 的减小量。
计算式为 \((w - w \div 2) \times f[i]\)。

//结构体存储
struct Node{
    int id,w;
  	bool operator < (const Node &nxt) const{
        return (w-w/2)*f[id]<(nxt.w-nxt.w/2)*f[nxt.id];
	}
};
priority_queue <Node> q; 
//统计
for(int i=1;i<n;i++){
    q.push((Node){i,w[i]});
    sum+=f[i]*w[i];
}

之后不断的减小 \(sum\) 直到 \(sum \le S\)。

while(sum>S){
	Node cur=q.top();
	q.pop();
	sum-=(cur.w-cur.w/2)*f[cur.id];
	ans++;
	q.push((Node){cur.id,cur.w/2});
}

最后注意一下多组数据记得清空。

完整代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-'){
			f=-1;
		}
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
void write(int x){
	if(x<0){
		putchar('-');
		x=-x;
	}
	if(x>9){
		write(x/10);
	}
	putchar(x%10+'0');
	return ;
}
const int N=1e5+5;
vector<int> g[N];
map<int,int> G[N];
int f[N],w[N];
int T,n,S,sum,ans,dp[N];
struct Node{
    int id,w;
	bool operator < (const Node &nxt) const{
    	return (w-w/2)*f[id]<(nxt.w-nxt.w/2)*f[nxt.id];
	}
};
priority_queue <Node> q; 
void dfs(int u,int fa){
	bool flag=0;
	for(int i=0;i<g[u].size();i++){
		int v=g[u][i];
		if(v!=fa){
			dfs(v,u);
			f[G[u][v]]=dp[v];
			dp[u]+=dp[v];
			flag=1;
		}
	}
	if(!flag){
		dp[u]=1;
	}
}
signed main(){
	T=read();
	while(T--){
		n=read();S=read();
        //记得清空
		while(!q.empty()){
			q.pop();
		}
		sum=ans=0;
		for(int i=1;i<=n;i++){
			g[i].clear();
			G[i].clear();
			f[i]=w[i]=dp[i]=0;
		}
        //读入+映射i
		int u,v;
		for(int i=1;i<n;i++){
			u=read();v=read();w[i]=read();
			g[u].push_back(v);
			g[v].push_back(u);
			G[u][v]=G[v][u]=i;//注意这里的映射，记得u到v和v到u都要映射
		}
		dfs(1,0);
		for(int i=1;i<n;i++){
			q.push((Node){i,w[i]});
			sum+=f[i]*w[i];
		}
		while(sum>S){
			Node cur=q.top();
			q.pop();
			sum-=(cur.w-cur.w/2)*f[cur.id];
			ans++;
			q.push((Node){cur.id,cur.w/2});
		}
		write(ans);
		puts("");
	}
	return 0;
}