第13章 最优化和线性化

1.最优化第一个例子

　　假设有个农场的边界是一道又长又直的篱笆，而这个农场主现在想要多圈一块地来喂马，但这个农场主有些古怪，想圈出一个直角三角形，并以之前的篱笆为一边(不是斜边)。

假设只有300英尺长的篱笆可用，并且农场主想使新圈出的地面积尽可能的大。那么这块地的周长和面积分别为多少？

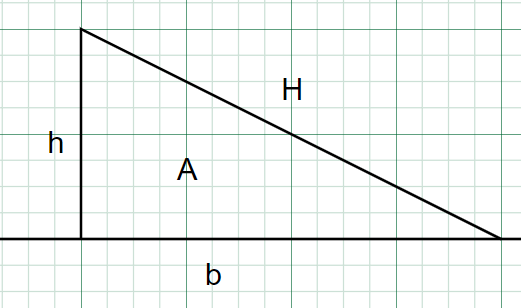
1.设三角形的底边为b,高为h,斜边为H,面积为A

2.篱笆长度为h+H,想要最优化面积A

$A = bh/2$

$h+H = 300$

$H^2 = h^2 + b^2$

所以：

$H = \sqrt{b^2 + h^2}$

$h+\sqrt{b^2 + h^2} = 300$

再将b消掉

$b^2 + h^2 = (300-h)^2$

$b^2 + h^2 = 90000 - 600h + h^2$

$b= \sqrt{90000 - 600h} = 10\sqrt{900-6h}$

原方程$A = bh/2$可以改写为

$A= 1/2*10\sqrt{900-6h}*h = 5h\sqrt{900-6h}$

 $dA/dh= (\dot{5h})*\sqrt{900-6h}+(5h)*(\dot{\sqrt{900-6h}}) = 45(100-h / (\sqrt{900-6h}))$

所以当$h = 100$时导数为0

$A = 5(100)\sqrt{900 - 6(100)} = 5000\sqrt{3}$

知道$h = 100$,周长就很好求了，但这个不是重点，当我们可以把面积与h的方程列出来的时候，可以在desmos上直接看看函数图像是什么样子的。