3.三种简单的力

1.重力

万有引力定律：

$F = G \frac{m_1 m_2}{r^2}$

实际在模拟时使用的方程：

$F = mg$(m是物体质量，g为指向向下的常数矢量)

2.摩擦力

2.1静摩擦力

当两个物体相对静止时，阻止它们开始运动的摩擦力称为静摩擦力。

$f_s = \mu_s N$

$ \mu_s$:静摩擦系数

$N$:法向力的大小

2.2动摩擦力

当两个物体相对运动时，阻止它们继续相对运动的摩擦力称为动摩擦力。

$f_k = \mu_k N$

$ \mu_k$:动摩擦系数

$N$:法向力的大小

3.弹簧力

胡克定律：

$f_r = k(l_reset - l)$

$l_reset$:弹簧静止长度

$l$:弹簧当前的长度

$k$:弹簧常数

3.1非阻尼振荡运动方程

$x(t) = A \cos(\omega t + \theta_0)$

$\dot{x}(t)=-A\omega \sin(\omega t + \theta_0)$

$\ddot{x}(t)=-A\omega^2 \cos(\omega t + \theta_0)$

 

使用虚拟弹簧不需要考虑弹簧常数或者质量，更多的时候是关心频率，所以将方程做变形：

$x(t) = A \cos(2 \pi F t + \theta_0)$

这个方程是真实物理中不存在的情况，这种情况下弹簧将永远振荡

 3.2阻尼振荡运动方程

现实中，至少还有两种力，一个是外力，一个是摩擦力，这些力的存在最终导致弹簧运动停止。

降低振荡系统振幅的效应的通用术语是阻尼。

阻尼力：与速度成正比，方向与速度相反：

$f_d = -c\dot{x}$

$f_d$:阻尼力的瞬时大小和方向

$\dot{x}$:瞬时速度

$c$:描述粘度，粗糙度等常数项

合力：

$f_{net} = f_r + f_d = -kx-c\dot{x}$

 求加速度：

利用牛顿第二定律

$f = ma$

$a = \frac{f}{m}$

$\ddot{x} = f_{net}/m = -\frac{k}{m} x - \frac{c}{m} \dot{x}$

 通过增加两个新量重写公式：

1.$\omega_0$:无阻尼角频率，$\omega_0 = \sqrt{\frac{k}{m}}$

2.$\zeta$:阻尼比，与阻尼系数，质量和无阻尼角频率有关，$\zeta = \frac{c}{2\sqrt{mk}} = \frac{c}{2m\omega_0}$

 带入方程：

$\ddot{x} = -\omega_0^2x - 2\zeta\omega_0\dot{x}$

这个方程是带有常系数的二阶线性齐次微分方程，有三种不同情况：欠阻尼、临界阻尼和过阻尼。

二阶齐次微分方程求解如下：

$a\ddot{x}(t) + b\dot{x}(t) + cx(t) = 0$

1.提取特征二次方程：$at^2 + bt +c = 0$

2.求解根

$\sqrt{b^2-4ac}<0$无实根; $\sqrt{b^2-4ac}=0$两个相同根，$\sqrt{b^2-4ac}>0$ 两个根

如果有两个不同的实根：$\alpha$和$\beta$

$y = Ae^{\alpha x} + Be^{\beta x}$

如果只有一个实根$\alpha x$

$y = Ae^{\alpha x} + Be^{\alpha x}$

如果有两个复根，他们共轭，$\alpha \pm i\beta$

$y = e^{\alpha x}(A\cos({\beta x})+B\sin({\beta x}))$

将我们要求解的微分方程带入：

$\ddot{y} = -\omega_0^2y-2\zeta\omega_0\dot{y}$

$\ddot{y} +2\zeta\omega_0\dot{y} + \omega_0^2y = 0$

特征方程 $t^2 + 2\zeta\omega_0 t + \omega_0^2 = 0$

$\sqrt{b^2-4ac}$ = $\sqrt{4\zeta^2\omega_0^2 - 4\omega_0^2}$ = $2\omega_0^2\sqrt{\zeta^2-1}$

情况1：无实根时,$0\leq \zeta < 1$,$\alpha = -\frac{2\zeta\omega_0}{2}=-\zeta\omega$;$\beta = \frac{\sqrt{4\omega_0^2 - 4\zeta^2\omega_0^2}}{2} = \omega_0\sqrt{1-\zeta^2}$

 带入$y = e^{\alpha x}(A\cos({\beta x})+B\sin({\beta x}))$

$y = e^{-\zeta\omega_0 x}(A\cos({\omega_0\sqrt{1-\zeta^2} x})+B\sin({\omega_0\sqrt{1-\zeta^2} x}))$

 令$\omega_d = \beta = \omega_0\sqrt{1-\zeta^2} $

$y = e^{-\zeta\omega_0 x}(A\cos({\omega_d x})+B\sin({\omega_d x}))$

所以方程如下：

$x(t) = e^{-\zeta\omega_0 t}(A\cos({\omega_d t})+B\sin({\omega_d t}))$

$\dot{x}(t) = (-A\sin({\omega_d t})\omega_d + B\cos({\omega_d t})\omega_d)e^{-\zeta\omega_0 t} + (A\cos({\omega_d t}) + B\sin({\omega_d t}))e^{-\zeta\omega_0 t}*(-\zeta\omega_0)$

$x(0) = A$

$\dot{x}(0) = B\omega_d + Ae^0 * (-\zeta\omega_0) = B\omega_d - \zeta\omega_0\dot{x}(0)$

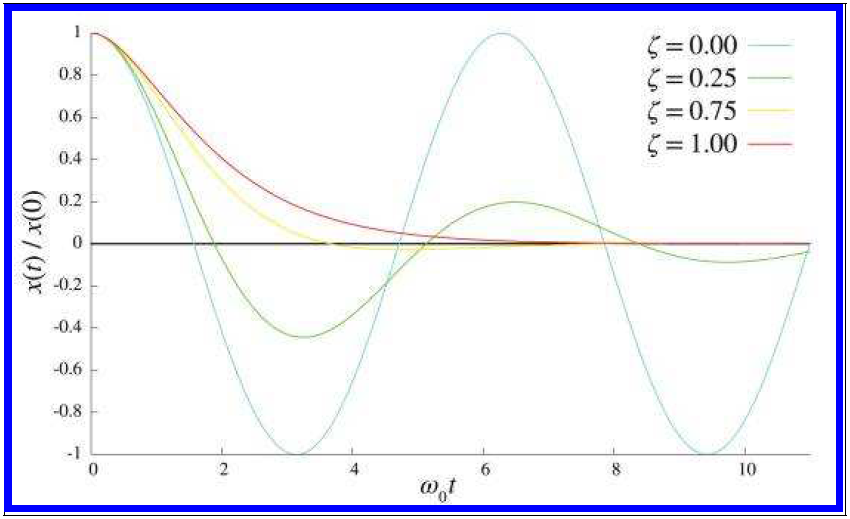
 所以:$A = x(0) $$B = \frac{\zeta\omega_0x(0)+\dot{x}(0)}{\omega_d}$ A和B由初始位置和速度决定，在这种情况下，系统欠阻尼，运动无期限振荡，振幅会随着时间推移呈指数衰减。

情况2:$\zeta = 1$时，方程如下：

$\alpha = -\frac{2\zeta\omega_0}{2} = -\omega_0$

$y = Ae^{-\omega_0 x} + Bxe^{-\omega_0 x} = (A+Bx)e^{-\omega_0 x}$

 所以：

$x(t) = Ae^{-\omega_0 t} + Bte^{-\omega_0 t} = (A+Bt)e^{-\omega_0 t}$

$\dot{x}(t) = Be^{-\omega_0 t} -\omega_0(A+Bt)e^{-\omega_0 t}$

 $x(0) = A$

$\dot{x}(0) = B-\omega_0A = B-\omega_0x(0)$

$B = \omega_0x(0) + \dot{x}(0)$

所以：$A = x(0) B =  \omega_0x(0) + \dot{x}(0)$,在这种情况下，振荡频率消失，称为临界阻尼的阈值，系统不再震荡，而是呈指数衰减。