超市

【超市】

【问题描述】

超市里有N件商品，每个商品都有利润pi和过期时间di,每天只能卖一件商品，过期商品（即当天di<=0）不能再卖。求合理安排每天卖的商品的情况下，可以得到的最大收益是多少。

【输入格式】

输入包含多组测试用例，测试用例最多30组。
每组测试用例，以输入整数N开始，接下里输入N对pi和di，分别代表第i件商品的利润和过期时间。
在输入中，数据之间可以自由穿插任意个空格或空行，输入至文件结尾时终止输入，保证数据正确。

【输出格式】

对于每组产品，输出一个该组的最大收益值。每个结果占一行。
【样例输入】
4 50 2 10 1 20 2 30 1
7 3 1 2 1 10 3 100 2 8 2 1 20 50 10

【样例输出】

80
169

数据范围

0≤N≤10000,1≤pi,di≤10000

分析：

每天只能卖一件，过期不能卖。我们的任务是合理规划商品的卖出日期，使得收益最大。

贪心：按利润大小顺序，规划卖出时间，尽可能晚点卖，这样可能会给保质期短的商品留有更多选择机会。

先将商品按利润从大到小排序，然后按顺序规划卖出日期。卖出时间为，可以卖出的日期中的最晚的那一天。

设:排序后第i件商品的利润是 a[i].p，过期天数是a[i].d。

计算第I号商品可以最晚卖出的日期，从过期天数a[i].d 往前查,排除那些已经卖过商品的日期后的最晚的那一天。

直接模拟会超时。怎样更快找到最晚可卖日期？

方法一：并查集

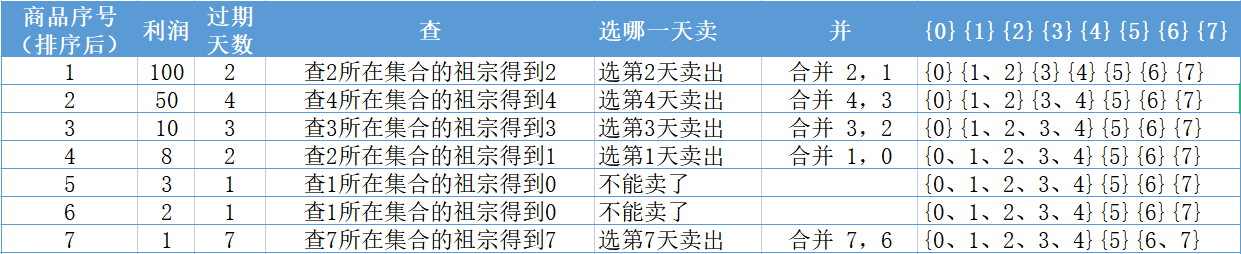
不断往前找的过程，很像并查集中不断向上找祖宗的过程。

起初我们把所有日期抽象为一个集合，集合的祖宗（也可以说是集合的代表元素）是自己 。

我们把最晚售卖日期当成把每个集合的祖宗，同时安排个0天的集合，若是有某个商品查到的祖宗是0，表示它这个商品已经没法卖了。

并查集中“并”：

当某个商品的保质期是d，我们计算出的最晚售卖时间是x，那么我们就将x,x-1 所在集合合并。

含义是，下一次再有保质期是d的商品出现时，它的最晚售卖时间最大可能是x-1，当然x-1 那一天可能也卖过商品了，那它最晚售卖时间就是x-2了。

 

#include <bits/stdc++.h>
using namespace std;
const int N = 10005;
int n, ans;
int f[N];
struct node {
    int t, val;
} a[N];
bool cmp(const node &x, const node &y) { return x.val > y.val; }
int find(int x) {
    if (f[x] < 0)
        return x;
    return f[x] = find(f[x]);
}
int main() {
    while (cin >> n) {
        ans = 0;
        memset(f, -1, sizeof(f));
        for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].val, &a[i].t);
        sort(a + 1, a + 1 + n, cmp);
        for (int i = 1; i <= n; i++) {
            int r1 = find(a[i].t);
            if (r1 > 0)
                ans += a[i].val, f[r1] = r1 - 1;
        }
        printf("%d\n", ans);
    }
    return 0;
}

  

方法二：贪心

贪心：

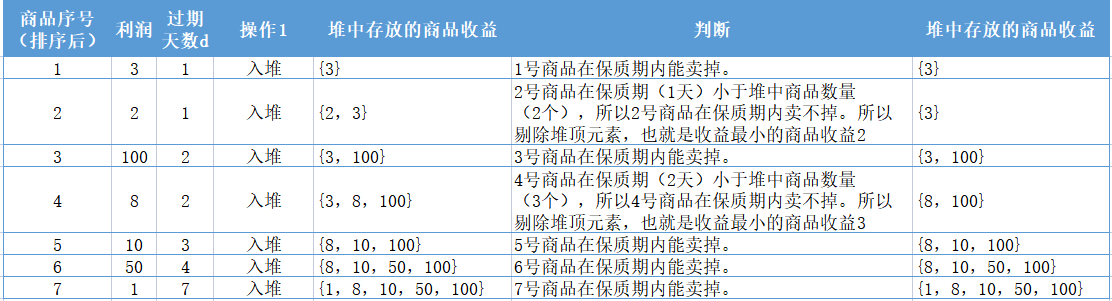
用小根堆（收益最小的商品在堆顶）来维护打算卖出的商品集合。

按保质期从小到大的顺序扫描商品：

（1）放入小根堆，

（2）若刚加入堆的商品在保质期内无法卖出，那剔除堆顶收益最小的商品，给新入堆商品腾出售卖日期。

扫描结束后，堆中的商品就是能得到最大总收益的商品集合。

 

 

#include <bits/stdc++.h>
using namespace std;
const int MAX = 100015;
typedef long long LL;
struct node {
    int p;
    int d;
} a[MAX];

bool cmp(const node &x, const node &y) { return x.d < y.d; }

int main() {
    int n;
    while (cin >> n) {
        for (int i = 1; i <= n; i++) {
            cin >> a[i].p >> a[i].d;
        }

        priority_queue<node, vector<int>, greater<int> > heap;

        //按保质期从小到大的顺序处理每个商品
        sort(a + 1, a + 1 + n, cmp);

        int ans = 0;
        for (int i = 1; i <= n; i++) {
            heap.push(a[i].p);
            ans += a[i].p;

            //优先队列中保存了准备卖出的商品收益，价值最小的在顶。
            //由于是按照保质期从小到大的顺序处理的
            //所以堆中的商品保质期一定都是小于等于a[i].d的

            //堆中的每个商品占用一个售卖日期
            //若其中的商品个数大于刚加入堆中的i号商品的保质期
            //那么刚加入堆中的i号商品将无法在保质期前卖出，（因之前的商品占去了所有可卖的日期）
            //所以需要就从堆中剔除一个商品，腾出一个售卖日期给新入商品
            //那剔除哪一个商品呢？
            //当然是剔除堆中收益最小的商品，也就是堆顶那个。
            //当然剔除也可能是刚刚加入的那个i号商品，那一定是因为它的价值在堆中最小

            if (heap.size() > a[i].d) {
                ans -= heap.top();
                heap.pop();  // 时间d 前保证卖掉 d 件商品  每次去掉最小的
            }
        }

        cout << ans << endl;
    }

    return 0;
}