直线段与圆弧光栅化的计算方法
直线段光栅化
数值微分法(DDA算法)
计算方法:
\(\Delta\)x = \(x_2-x_1\),\(\Delta y=y_2-y_1\) ,\(k=\frac{\Delta y}{\Delta x}\)
当$ -1≤k≤1 $ 时:
\[\begin{array}{l}
\left\{\begin{matrix}
x_{i+1} = x_i + 1 \quad \\
y_{i+1} = y_i + k \quad \\
\end{matrix}\right.
\end{array}
\]
当 $ k>1 $ 时:
\[\begin{array}{l}
\left\{\begin{matrix}
x_{i+1} = x_i + \frac{1}{k} \quad \\
y_{i+1} = y_i + 1 \quad \\
\end{matrix}\right.
\end{array}
\]
当$ k<-1 $ 时:
\[\begin{array}{l}
\left\{\begin{matrix}
x_{i+1} = x_i - \frac{1}{k} \quad \\
y_{i+1} = y_i - 1 \quad \\
\end{matrix}\right.
\end{array}
\]
算法评价:
- 比直接使用\(y=kx+b\)更快
- 耗时(增加了浮点数运算,除法运算,取整操作等,不利于硬件实现)
\(Bresenham\)划线算法(重点掌握)
计算方法:
\(\Delta\)x = \(x_2-x_1\),\(\Delta y=y_2-y_1\) ,\(k=\frac{\Delta y}{\Delta x}\) \(d_i=\Delta x(s_i-t_i)\)
- 当$ 0<k≤1 $ 时:
\(d_0 = 2dy -dx\)
绘制点的递推公式:
\[\begin{array}{l}
\left\{\begin{matrix}
x_{i+1} = x_i + 1 \quad \\
y_{i+1} = y_i + \Delta y \quad
\begin{array}{l}
\left\{\begin{matrix}
\Delta y = 0 \quad d_i<0 \\
\Delta y = 1 \quad d_i≥0 \\
\end{matrix}\right.
\end{array} \\
\end{matrix}\right.
\end{array} \\
\]
误差项递推公式:
\[d_{i+1}=
\begin{array}{l}
\left\{\begin{matrix}
d_i + 2(dy-dx) \quad d_i≥0\\
d_i + 2dy \quad d_i<0
\end{matrix}\right.
\end{array}
\]
-
当 $ 1<k $ 时:
\(d_0 = 2dx -dy\)
绘制点的递推公式:\[\begin{array}{l} \left\{\begin{matrix} y_{i+1} = y_i + 1 \quad \\ x_{i+1} = x_i + \Delta x \quad \begin{array}{l} \left\{\begin{matrix} \Delta y = 0 \quad d_i<0 \\ \Delta y = 1 \quad d_i≥0 \\ \end{matrix}\right. \end{array} \\ \end{matrix}\right. \end{array} \] 误差项递推公式:
\[d_{i+1}= \begin{array}{l} \left\{\begin{matrix} d_i + 2(dx-dy) \quad d_i≥0\\ d_i + 2dx \quad d_i<0 \end{matrix}\right. \end{array} \]-
当 $ 1<k $ 时:
\(d_0 = 2dx -dy\)
绘制点的递推公式:\[\begin{array}{l} \left\{\begin{matrix} y_{i+1} = y_i + 1 \quad \\ x_{i+1} = x_i + \Delta x \quad \begin{array}{l} \left\{\begin{matrix} \Delta y = 0 \quad d_i<0 \\ \Delta y = 1 \quad d_i≥0 \\ \end{matrix}\right. \end{array} \\ \end{matrix}\right. \end{array} \] 误差项递推公式:
\[d_{i+1}= \begin{array}{l} \left\{\begin{matrix} d_i + 2(dx-dy) \quad d_i≥0\\ d_i + 2dx \quad d_i<0 \end{matrix}\right. \end{array} \]
-
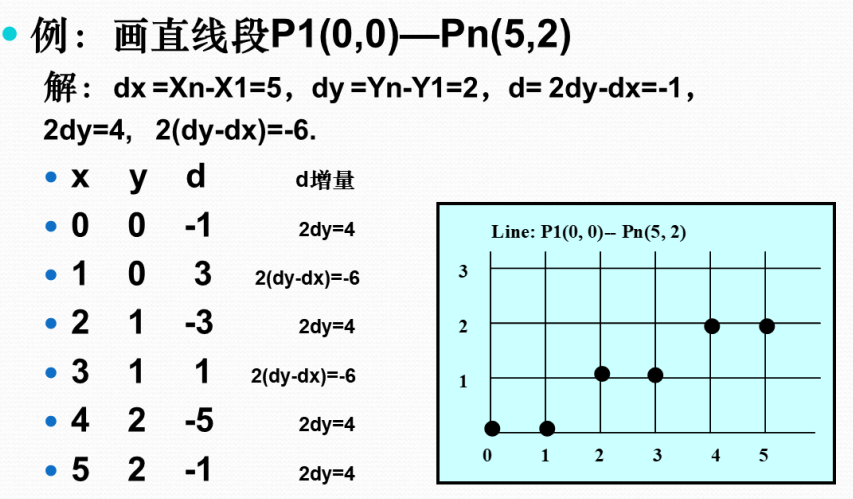
注意: 感觉期末只可能考察斜率在 \(0\)~\(1\)之间且起点从原点开始的
若dx > 0, dy > 0, 0< m < 1:
xi = x1, yi = y1
第一项: pi = 2dy -dx
若pi < 0: pi = pi + 2dy, yi = yi
若pi > 0: pi = pi + 2dy - 2dx, yi = yi + 1
xi = xi + 1
输出: (xi, yi)
若dx > 0, dy > 0, m > 1:
xi = x1, yi = y1
第一项: pi = 2dx -dy
若pi < 0: pi = pi + 2dx, xi = xi
若pi > 0: pi = pi + 2dx - 2dy, xi = xi + 1
yi = yi + 1
输出: (xi, yi)
若dx > 0, dy < 0, 0< m < 1:
xi = x1, yi = -y1
第一项: pi = 2dy -dx
若pi < 0: pi = pi + 2dy, yi = yi
若pi > 0: pi = pi + 2dy - 2dx, yi = yi + 1
xi = xi + 1
输出: (xi, -yi)
若dx > 0, dy < 0, m > 1:
xi = x1, yi = -y1
第一项: pi = 2dx -dy
若pi < 0: pi = pi + 2dx, xi = xi
若pi > 0: pi = pi + 2dx - 2dy, xi = xi + 1
yi = yi + 1
输出: (xi, -yi)
若dx < 0, dy > 0, 0< m < 1:
xi = -x1, yi = y1
第一项: pi = 2dy -dx
若pi < 0: pi = pi + 2dy, yi = yi
若pi > 0: pi = pi + 2dy - 2dx, yi = yi + 1
xi = xi + 1
输出: (-xi, yi)
若dx < 0, dy > 0, m > 1:
xi = -x1, yi = y1
第一项: pi = 2dx -dy
若pi < 0: pi = pi + 2dx, xi = xi
若pi > 0: pi = pi + 2dx - 2dy, xi = xi + 1
yi = yi + 1
输出: (-xi, yi)
若dx < 0, dy < 0, 0< m < 1:
xi = -x1, yi = -y1
第一项: pi = 2dy -dx
若pi < 0: pi = pi + 2dy, yi = yi
若pi > 0: pi = pi + 2dy - 2dx, yi = yi + 1
xi = xi + 1
输出: (-xi, -yi)
若dx < 0, dy < 0, m > 1:
xi = -x1, yi = -y1
第一项: pi = 2dx -dy
若pi < 0: pi = pi + 2dx, xi = xi
若pi > 0: pi = pi + 2dx - 2dy, xi = xi + 1
yi = yi + 1
输出: (-xi, -yi)
评价方法:
- 只有整数运算,不含乘除法
- 只有加法和乘2运算,效率高
中点划线算法(重点掌握)
计算方法:(假定\(0≤k≤1\) ,\(x\)是最大位移方向)
\(d_i = F(M) = y_i+0.5-k(x_i+1)-b\)
绘制点的递推公式:
\[\begin{array}{l}
\left\{\begin{matrix}
x_{i+1} = x_i + 1\\
y_{i+1} = \begin{array}{l}
\left\{\begin{matrix}
y_{i} + 1 \quad d<0 \\
y_{i} \quad d≥0
\end{matrix}\right.
\end{array}
\end{matrix}\right.
\end{array}
\]
误差项递推公式:
\(d_1 = 0.5 - k\)
\[d_{i+1}=
\begin{array}{l}
\left\{\begin{matrix}
d_i + 1 - k \quad d_i<0\\
d_i - k \quad d_i≥0
\end{matrix}\right.
\end{array}
\]
改进的计算方法:(假定\(0≤k≤1\) ,\(x\)是最大位移方向)
用 \(2d\Delta x\) 代替 \(d\) ,令\(D=2d\Delta x\)
绘制点的递推公式:
\[\begin{array}{l}
\left\{\begin{matrix}
x_{i+1} = x_i + 1\\
y_{i+1} = \begin{array}{l}
\left\{\begin{matrix}
y_{i} + 1 \quad d<0 \\
y_{i} \quad d≥0
\end{matrix}\right.
\end{array}
\end{matrix}\right.
\end{array}
\]
误差项递推公式:
\(D_1 = \Delta x - 2\Delta y\)
\[D_{i+1}=
\begin{array}{l}
\left\{\begin{matrix}
D_i + 2\Delta x - 2\Delta y \quad D_i<0\\
D_i- 2\Delta y \quad D_i≥0
\end{matrix}\right.
\end{array}
\]
圆弧光栅化
八分法画圆
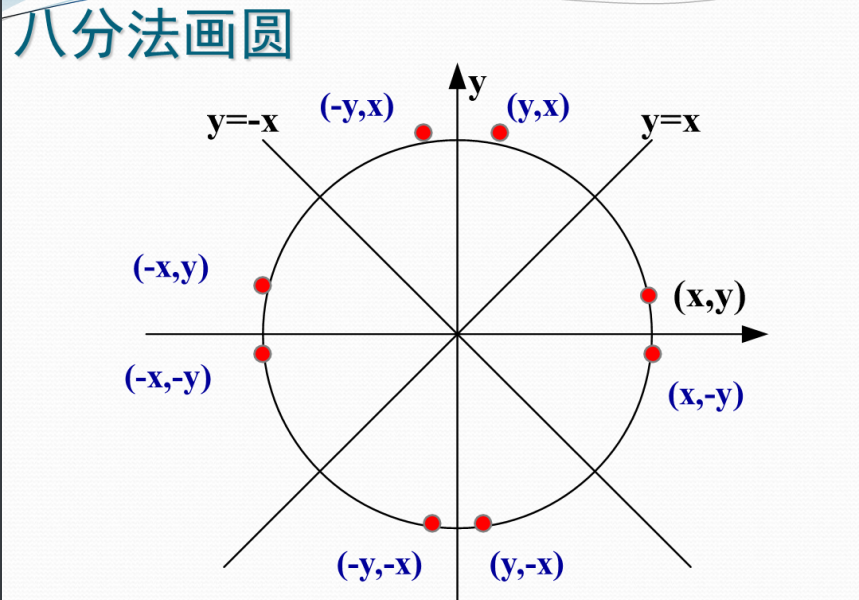
中点画圆算法
计算方法:
- 误差项
\[d = F(x_M,y_M)=F(x_i+1,y_i-0.5)=(x+1)^2+(y_i-0.5)^2-R^2
\]
- \(d<0\)时,下一点取\(Pu(x_i+1,y_i)\)
- \(d_i≥0\)时,下一点取\(Pd(x_i+1,y_i-1)\)
\(初项:d_0 =1.25-R\)
\[d_{i+1}=
\begin{array}{l}
\left\{\begin{matrix}
d_i + 2x_i + 3 \quad d_i<0\\
d_i + 2(x_i-y_i) + 5 \quad d_i≥0
\end{matrix}\right.
\end{array}
\]
改进计算方法:
用\(e=d-0.25代替d\)
\(初项:e_0 =1-R\)
\[e_{i+1}=
\begin{array}{l}
\left\{\begin{matrix}
e_i + 2x_i + 3 \quad e_i<0\\
e_i + 2(x_i-y_i) + 5 \quad e_i≥0
\end{matrix}\right.
\end{array}
\]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号