BUAA-OO-U1-Summary
BUAA-OO-U1-Summary
1 问题描述
第一单元中，我们所要解决的问题是表达式化简，即“去括号”。
由于原表达式中可能出现乘方、自定义函数、三角函数、求和函数等形式以及相互之间的嵌套，因此，如何在去括号、函数带入的同时保证形式的标准，并尽可能简化结果，是需要解决的重点问题。
2 整体结构
表达式化简的过程总体来看就是一个字符串读取、解析、合并与化简的过程。因此，我所建立的架构，由Lexer 、 Parser 、 Expression 、 Function 四部分组成，并在 MainClass 中相互作用得到结果。各部分的功能大致如下：
| 类 | 作用 |
|---|---|
| Lexer | 读取输入的字符串，并进行分割得到具有完整意义的子串 |
| Parser | 解析子串，并按照相应层次构建表达式结构 |
| Factor | 存储表达式的结构，由Expr、Term、Factor三个层次构成 |
| Function | 对自定义函数进行解析，并在初始串中进行替换 |
各部分间关系如下图：
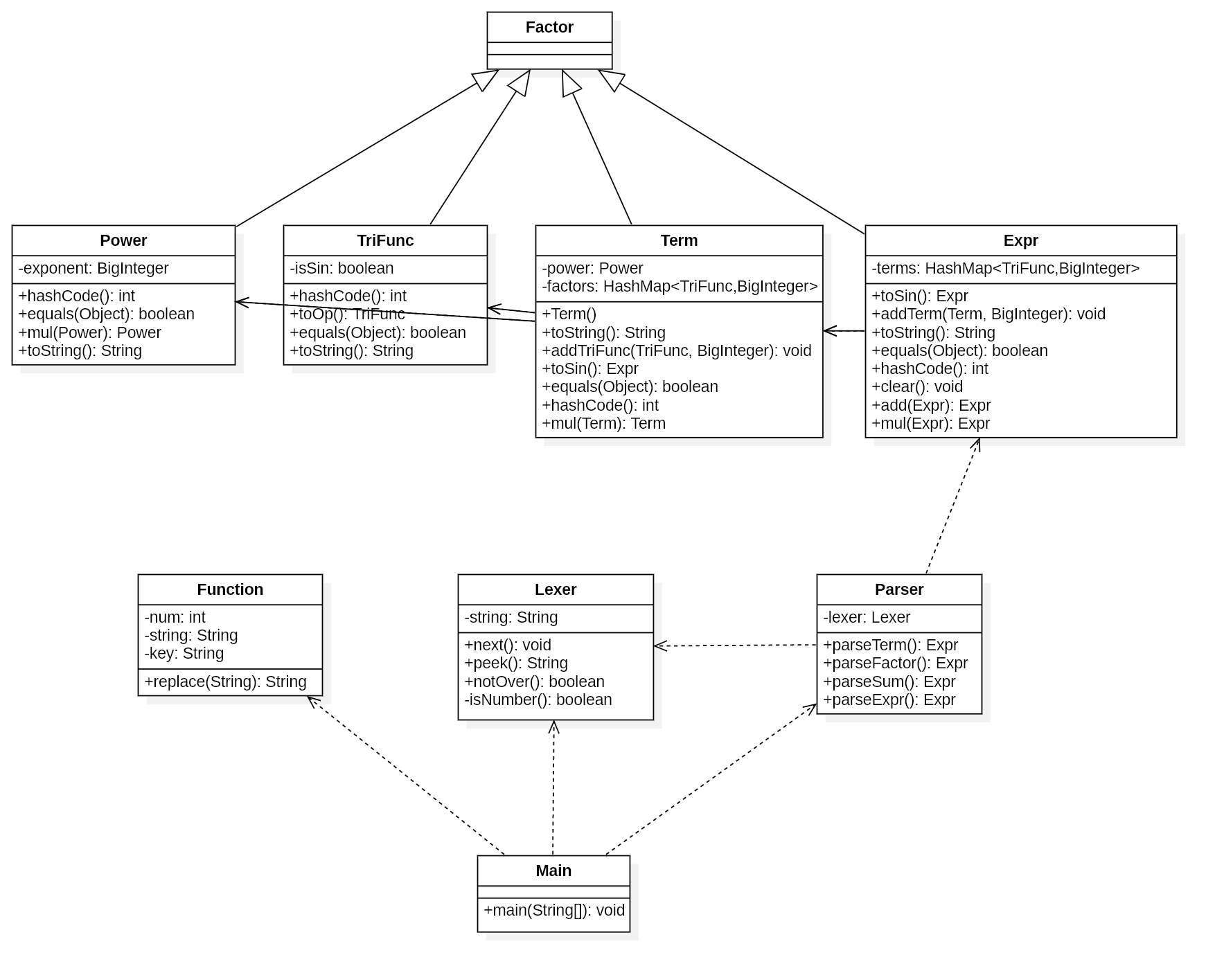
3 总体流程
首先进行自定义函数的读取，并建立对应的 Function 类；
然后读入初始字符串，并利用 Function 类对其进行函数带入；
利用处理后的字符串建立 Lexer 类；
建立 Parser 类，对前一步建立的 Lexer 类进行解析并得到 Expression 类；
Expression 类对结果进行化简后转化为字符串输出。
4 迭代过程
三次作业中我的整体架构几乎没有改动，主要的变动为
-
Term以下增加了TriFunc类： 第一次作业中我直接将
Term利用 $term=a*x^b$ 的标准形式，将Factor直接识别为Term进行处理；第二次作业中，新增了TriFunc类，用HashMap容器保存某一形式的三角函数对其指数的映射。 -
增加了与
Main直接相关的Function类： 第二次作业中，为了实现自定义函数的代入，新增了
Function类，其作用主要为识别自定义函数的自变量并进行变量到函数串、函数串到主串间的字符串替换；
4 分析
首先是类复杂度的分析：
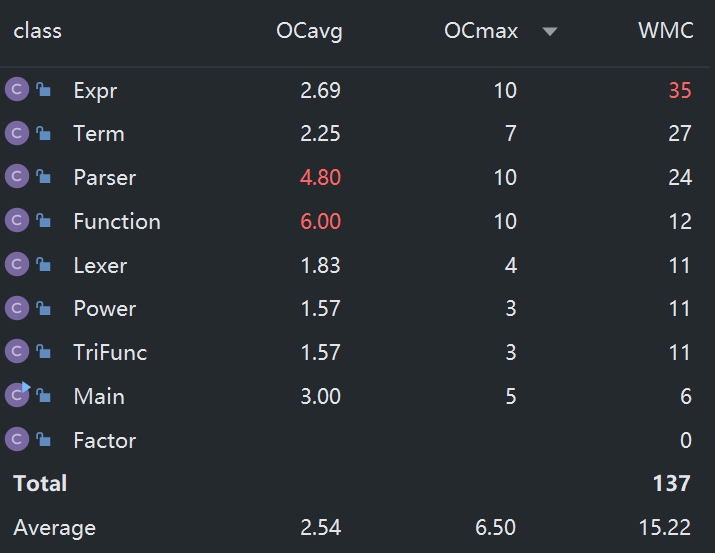
其次是方法复杂度的分析：
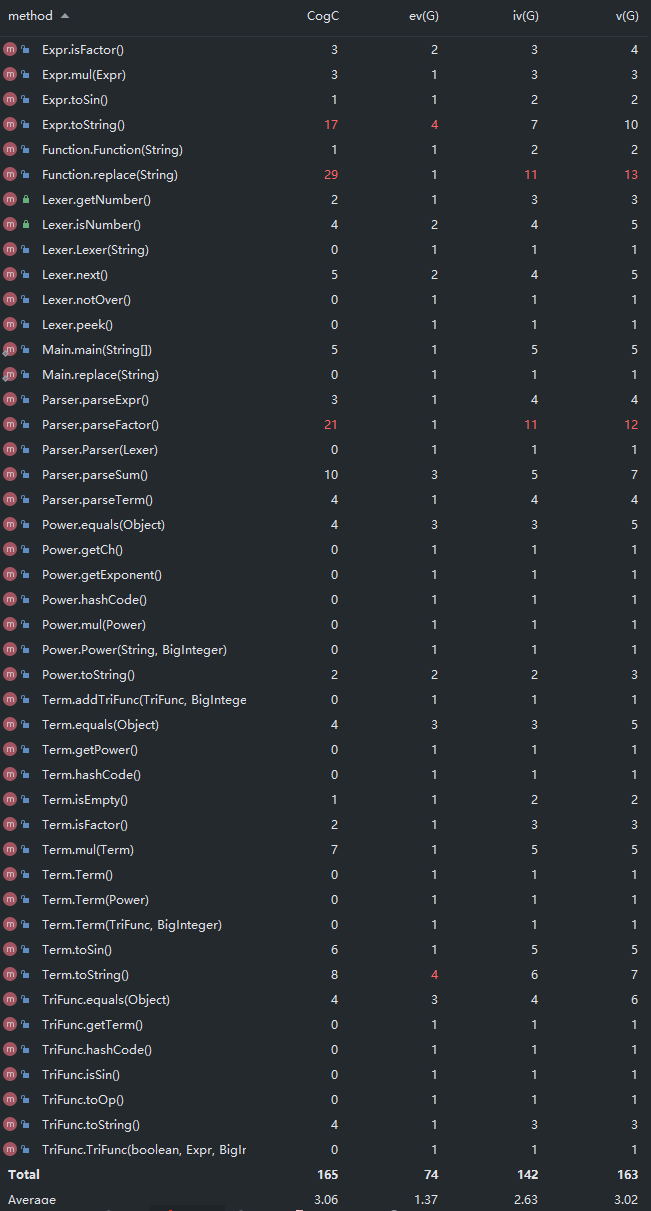
可以看出，类和方法的整体复杂度均较低，复杂度高的主要是 Function 、 Expr 、 Parser 三个类，主要原因为：
Function类内需要实现两个字符串替换，同时还要利用栈进行括号匹配的比较，因此代码较长、复杂度较高；Expr类内需要实现最高层的toString()方法，需要进行多种情况的判断；Parser类需要实现基元识别的parseFactor方法，由于基元形式较多，因此代码复杂度较高。
5 强测总结
本单元实验在强测中出现的仅有bug为第二次作业中，未实（发）现 sin() 和 cos() 内为常数的情况 实在想不到中测中竟然连一个这样的数据都没有 ，所以第二次作业直接爆炸，修改的话，直接将 Parser 中三角函数内部的表达式利用 ParseExpr 或 ParseTerm 进行解析 而不是解析power ，并在最后 toString() 时进行一个简单的判断即可。
所以读题还是很重要的...
6 互测总结
本单元的互测自己出现的bug同上。
对于互测，本单元中我并没有使用数据生成器进行大范围的评测，也没有实现一个数据对其余人均进行测试的评测机，因此互测积极性不够强，只是根据房间内同学们的架构自行构建了几个该架构中可能出现的问题，一一测试，太麻烦了。
下周一定写个评测机XP。
7 个人总结
本单元的麻烦之处主要在于第一周整体架构的建立(同时要做pre)和第二周优化的实现，第三周的递归自定义函数其实可以很轻松的解决。
而出现的bug主要是因为时间安排不当，最后一天才写导致过于仓促，优化不完全，还出现了题目理解问题等这些本可以避免的问题。
同时，测评机也是一个很方便的工具，懒得写测评机会导致更大的麻烦，因此要主动寻找简化工作的方法。
