四则运算

一.基本信息

这个作业属于哪个课程	软件工程
这个作业要求在哪	作业要求
这个作业的目标	实现四则运算

参与人员	姓名	学号
1	雷三鉴	3119009435
2	余子航	3119009444

Github项目地址

二.PSP

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	600	750
· Estimate	· 估计这个任务需要多少时间	10	10
· Analysis	· 需求分析 (包括学习新技术)	10	10
· Design Spec	· 生成设计文档	10	10
· Design Review	· 设计复审 (和同事审核设计文档)	30	40
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	30
· Design	· 具体设计	90	110
· Coding	· 具体编码	300	360
· Code Review	· 代码复审	30	60
· Test	· 测试（自我测试，修改代码，提交修改）	90	120
Reporting	报告	90	90
· Test Report	· 测试报告	10	10
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	70	70
合计		690	840

三.效能分析

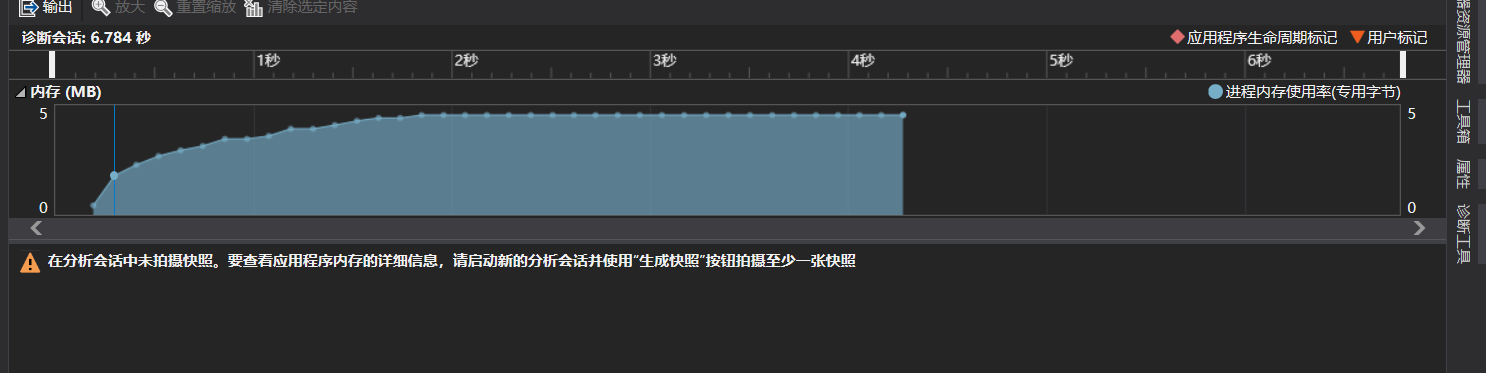
以下图片展示的是生成一万个等式的资源消耗截图

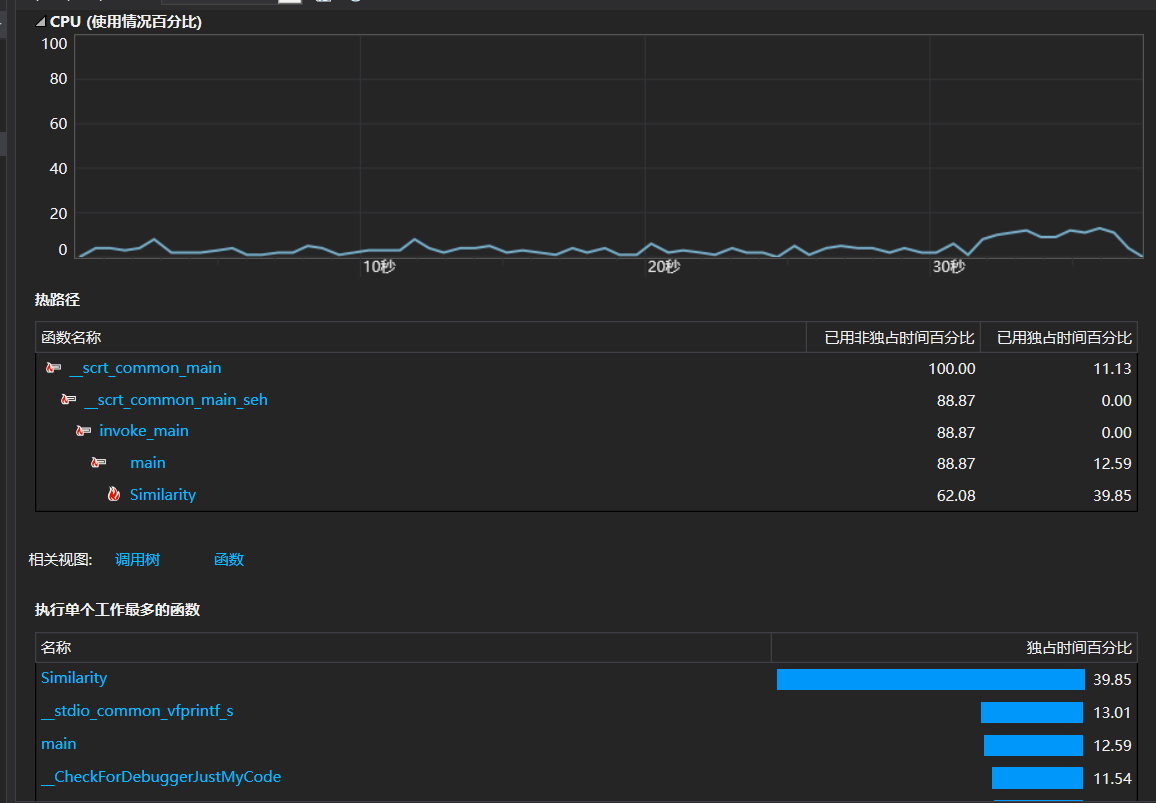
运算时间与内存占用

可以看到调用次数最多的是similarity函数，因为为了确定某一生成的式子是否与之前生成的式子相同，我们需要将式子与之前生成的式子进行比较，所以similarity函数调用的最多。
改进方法：
由于两个式子相同的必要条件是根结点的运算符以及值必须完全一致，所以我们可以利用哈希算法将根节点运算符以及其值单映射为一个哈希值，利用哈希值来进行索引
，由于根结点的运算符以及值完全一致的概率很低，所以similarity函数在调用的期望值上极大程度的降低了，同时，由于加了索引，在一般情况下，该函数的调用次数也被降低了很多。
但是空间消耗变大了，如上所说，根结点的运算符以及值完全一致的概率很低，而我们的哈希算法又是单射函数，这会导致该算法需要接近于线性的空间复杂度，考虑到现今计算机
的cpu发展速度远大于内存，该算法并不显得更好。所以，可以考虑只使用值来建立索引。

四.设计实现过程

项目结构

1生成等式树

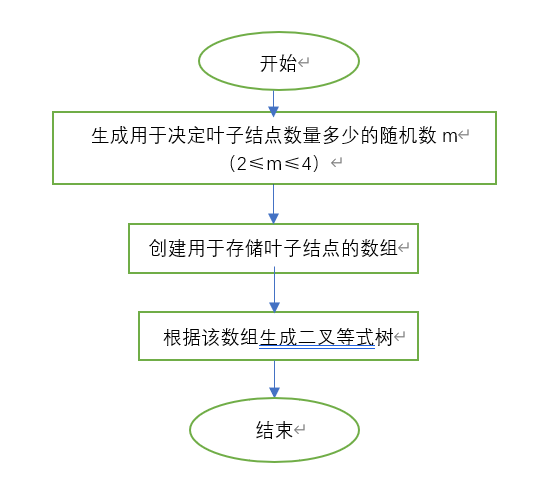
2判重
引入定义：树相似 对于两棵树A与B，若在B树上存在一个非叶结点的集合，对该集合每个元素的左右子树进行一次交换，A全等于B，则AB相似
利用树相似的性质可以判断等式重复
定理：若两棵用于表达中缀表达式A‘，B’的二叉等式树A和B相似,则A‘可以通过有限次交换得到B’（精力有限，以下给出非严格证明）
证明：任何中缀表达式可以递归的定义为：（左子中缀表达式）（运算符）（右子中缀表达式）
在用于表达中缀表达式的二叉等式树中，非叶结点代表运算符，而非叶结点的左子树代表左子中缀表达式，右子树代表右子中缀表达式，将该非叶结点的左右子树交换等价于将该运算符左右两边的子中缀表达式调换，这样的操作可以递归的进行，所以两棵用于表达中缀表达式 A‘，B’的二叉等式树A和B相似,则A‘可以通过有限次交换得到B’
所以通过判断该任意两棵二叉等式树是否相似可以判断等式是否重复。

以上证明过程是默认运算符为加号或者乘号，若运算符为减号或者除号，由于这两个运算符不满足交换律，则规定：若运算符为减号或者除号，则在这两颗二叉等式树中，该运算符所在结点的左右子树必须完全一致才为相似，否则不相似。

例子：
A’：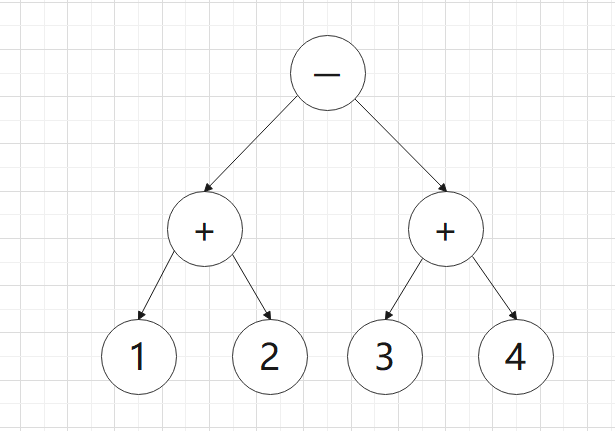

B’：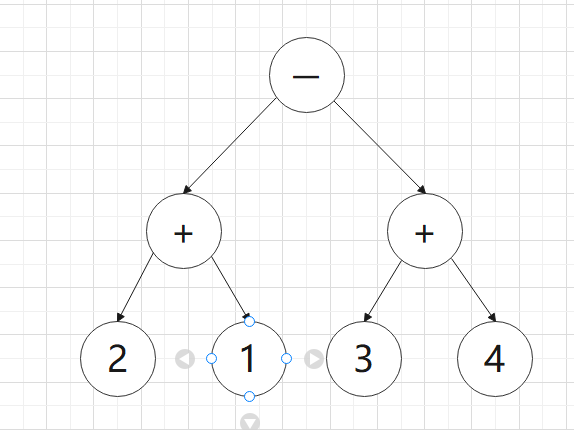

C’：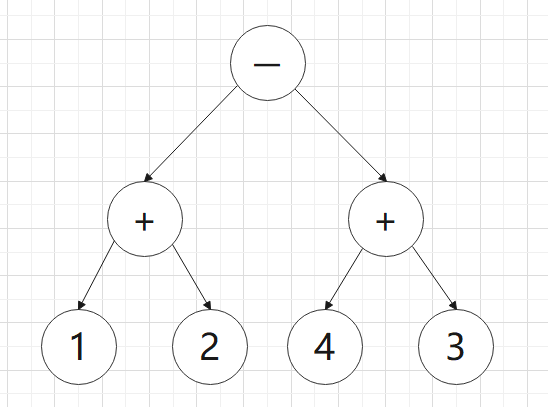

D’：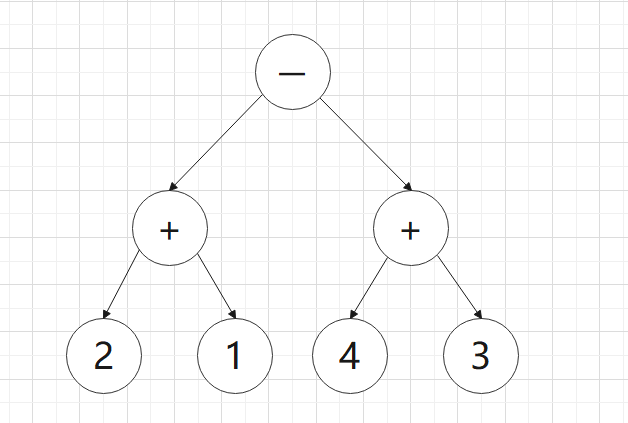

由上A‘二叉等式树交换非叶结点可得到B’，C‘，D’三个相似的二叉等式树，将四个二叉等式树转换成中缀表达式可得

A：（1+2）-（3+4）
B：（2+1）-（3+4）
C：（1+2）-（4+3）
D：（2+1）-（4+3）
以上四个中缀表达式，我们可以发现为重复的中缀表达式，所以可以得出，若二叉等式树之间可以通过交换非叶结点导致一致，即证明了二叉等式树相似，则二叉等式树转化成的中缀表达式属于重复

3.输出

五.核心代码说明

生成二叉等式树代码（GenerateTree）

点击查看代码

#include "head.h"


int Greatest_Common_Devisor(int var, int var1) {
	int devisor = 1;
	int bigger_Num = (var > var1 ? var : var1);
	int smaller_Num = var + var1 - bigger_Num;

	if (bigger_Num % smaller_Num == 0) {
		return  smaller_Num;
	}

	for (int i = 1; i <= smaller_Num / 2; i++) {
		if (smaller_Num % i == 0)
			if (bigger_Num % i == 0) {
				devisor = i;
			}
	}

	return devisor;
}

void Creat_Operator(EquationTreeNode*& t)
{
	int i = rand() % 4;
	switch (i)
	{
	case 0: t->operater = '+';
		break;
	case 1: t->operater = '-';
		break;
	case 2: t->operater = '*';
		break;
	case 3: t->operater = '/';
		break;
	default:
		break;
	}
}

void ExchangeChild(EquationTreeNode*& t) {
	
	EquationTreeNode* p = t->lchild;
	t->lchild = t->rchild;
	t->rchild = p;
}

EquationTreeNode* GenerateNumArray(int mount, int bound) {
	EquationTreeNode* NumArray = (EquationTreeNode*)malloc(mount * sizeof(EquationTreeNode));
	int s;
	int devisor;
	for (int i = 0; i < mount; i++) {
		s = rand() % 4;
		if (s == 0) {
			NumArray[i].lchild = NULL;
			NumArray[i].rchild = NULL;
			NumArray[i].operater = '\0';

			NumArray[i].numerator = rand() % 10 + 1;
			NumArray[i].denominator = rand() % 10 + NumArray[i].numerator / bound + 1;
			devisor = Greatest_Common_Devisor(NumArray[i].numerator, NumArray[i].denominator);
			NumArray[i].numerator /= devisor;
			NumArray[i].denominator /= devisor;

			NumArray[i].value = (double)NumArray[i].numerator / (double)NumArray[i].denominator;
		}
		else {
			NumArray[i].lchild = NULL;
			NumArray[i].rchild = NULL;
			NumArray[i].operater = '\0';

			NumArray[i].numerator = rand() % bound + 1;
			NumArray[i].denominator = 1;

			NumArray[i].value = (double)NumArray[i].numerator;
		}

	}

	return NumArray;
}

EquationTreeNode* GenerateTree(int bound, EquationTreeNode* &NumArrayRoot) {
	int mount = rand()%3+2; 
	int devisor;
	EquationTreeNode* NumArray = GenerateNumArray(mount, bound);
	NumArrayRoot = NumArray;

	EquationTreeNode* s = NumArray;
	EquationTreeNode* root = NULL;

	for (int i = 1; i < mount ; i++) {

	    root = (EquationTreeNode*)malloc(sizeof(EquationTreeNode));
		Creat_Operator(root);
		root->lchild = s;
		root->rchild = NumArray + i;
		 
		if ((root->lchild->value < root->rchild->value) && root->operater == '-') {
			ExchangeChild(root);
		}

		if ((root->lchild->value > root->rchild->value) && root->operater == '/') {
			ExchangeChild(root);
		}

		switch (root->operater)
		{
		case'+':root->value = root->lchild->value + root->rchild->value;

				root->numerator = root->lchild->numerator * root->rchild->denominator
								+ root->rchild->numerator * root->lchild->denominator;
				root->denominator = root->lchild->denominator * root->rchild->denominator;

				//约分
				if (root->numerator != 0)
				{
					devisor = Greatest_Common_Devisor(root->numerator, root->denominator);
					root->numerator /= devisor;
					root->denominator /= devisor;
				}

			break;
		case'-':root->value = root->lchild->value - root->rchild->value;
				
				root->numerator = root->lchild->numerator * root->rchild->denominator 
					              - root->rchild->numerator * root->lchild->denominator;
				root->denominator = root->lchild->denominator * root->rchild->denominator;

				//约分
				if (root->numerator!=0)
				{
					devisor = Greatest_Common_Devisor(root->numerator, root->denominator);
					root->numerator /= devisor;
					root->denominator /= devisor;
				}

			break;
		case'*':root->value = root->lchild->value * root->rchild->value;

			    root->numerator = root->lchild->numerator * root->rchild->numerator;
			    root->denominator = root->lchild->denominator * root->rchild->denominator;

				//约分
				if (root->numerator != 0)
				{
					devisor = Greatest_Common_Devisor(root->numerator, root->denominator);
					root->numerator /= devisor;
					root->denominator /= devisor;
				}

			break;
		case'/':
			  if ( root->rchild->value != 0) {
				   root->value = root->lchild->value / root->rchild->value;
			  }
			  else
			  {
				  Free(root);
				  free(NumArrayRoot);
				  return GenerateTree(bound,NumArrayRoot);
			  }
			    
			    root->numerator = root->lchild->numerator * root->rchild->denominator;
				root->denominator = root->lchild->denominator * root->rchild->numerator;

				//约分
				if (root->numerator != 0)
				{
					devisor = Greatest_Common_Devisor(root->numerator, root->denominator);
					root->numerator /= devisor;
					root->denominator /= devisor;
				}

			break;
		default:
			break;
		}

		s = root;
	}

	return root;
}

GenerateTree代码说明

Greatest_Common_Devisor 用于找到最大公约数进行约分，可用辗转相除法，但我们没有选择使用。
ExchangeChild函数在左子树的值小于右子树的值并且父结点的运算符为‘—’或者左子树的值大于右子树的值并且父结点的运算符为‘/’的情况下使用，
以保证运算过程中不会出现负数或者假分数的情况。
在case'/'的分支下，若发现该结点的右子树的值为0，说明生成了错误的等式树，则释放空间并重新生成等式树

判重（Similarity）代码

点击查看代码

#include"head.h"


bool Similarity(EquationTreeNode* tree, EquationTreeNode* tree1) {

	bool isSimilar;

	if (tree == NULL && tree1 == NULL) {
		return True;
	}

	if (tree->value != tree1->value || tree->operater != tree1->operater) {
		 return Fales;
	}


	if (tree->operater == '\0' && tree1->operater == '\0') {
		if (tree->value == tree1->value) {
			return True;
		}
		return Fales;
	}

	 if((tree->operater == '+' && tree1->operater == '+' || tree->operater == '*' && tree1->operater == '*'))
	{
		
		if ((tree->lchild->operater == tree1->lchild->operater && tree->rchild->operater == tree1->rchild->operater) 
			&& (tree->lchild->value == tree1->lchild->value && tree->rchild->value == tree1->rchild->value)) 
		{
		
			isSimilar = True;
			isSimilar = Similarity(tree->lchild, tree1->lchild);
			isSimilar = Similarity(tree->rchild, tree1->rchild);
			
			return isSimilar;

		}
		if ((tree->lchild->operater == tree1->rchild->operater && tree->rchild->operater == tree1->lchild->operater)
			&& (tree->lchild->value == tree1->rchild->value && tree->rchild->value == tree1->lchild->value))
		{
			
	
			isSimilar = True;
			isSimilar = Similarity(tree->lchild, tree1->rchild);
			isSimilar = Similarity(tree->rchild, tree1->lchild);
			
			return isSimilar;
		}
		
		return Fales;
	}

	 if (tree->operater == '-' && tree1->operater == '-' || tree->operater == '/' && tree1->operater == '/') {
	
		 if ((tree->lchild->value != tree1->lchild->value || tree->rchild->value != tree1->rchild->value)
			 || (tree->lchild->operater != tree1->lchild->operater || tree->rchild->operater != tree1->rchild->operater))
		 {
	
			 return Fales;
		 }
		 else
		 {
	
			 isSimilar = True;
			 isSimilar = Similarity(tree->lchild, tree1->lchild);
			 isSimilar = Similarity(tree->rchild, tree1->rchild);
		
			 return isSimilar;
		 }

	 }

	 return Fales;

}

void Free(EquationTreeNode* t) {
	if (t == NULL) return;

	if (t->operater!='\0') {
		if (t->lchild->operater!='\0') {
			Free(t->lchild);
		}
		if (t->rchild->operater != '\0') {
			Free(t->rchild);
		}
		free(t);
		
	}
	return;
}

similarity代码说明

基于判断两棵二叉等式树是否相似的思想，我们进行如下设计：
1、从根结点同时向下开始进行递归判断。
2、若在这两棵树的某对非叶结点的运算符为加号或者乘号时，我们则需要判断其中一个结点的左孩子的运算符以及该结点的值是否与另一个结点的左孩子或右孩子相对应的值相等，若前者的左孩子的运算符以及该结点的值等于后者的左孩子的运算符以及该结点的值则将isSimilar置为true，并继续向下递归。若前者的左孩子的运算符以及该结点的值等于后者的右孩子
的运算符以及该结点的值，则将isSimilar设置为true，然后让tree1的左子树和tree1的右子树比较，tree1的右子树和tree1的左子树比较。
3、最后返回isSimilar。

free函数说明

由于使用malloc函数来开辟叶子结点的存储空间，所以在free的过程中是不能直接将二叉等式树的叶子结点释放空间，否则编译器会提示访问权限冲突，所以在释放二叉等式树空间的过程中
若遇到运算符为'\0'的结点，则说明该结点为叶结点，直接返回。在操作符为非'\0'的情况下，先递归释放左子树的空间，再递归释放右子树的空间，最后释放该结点的空间。等到非叶结点释放完毕之
后，再单独释放由malloc函数开辟的空间。

六.测试运行

一万条四则运算的生成截图

七.项目小结

此次结对项目，体会了结对编程的优势，可以帮助对方走出思维死区，更快的找出bug。同时两人通过交换意见也可以提出比较好的算法。