首次个人作业
个人项目
| 这个作业属于哪个课程 | 软件工程 |
|---|---|
| 这个作业要求在哪 | 作业要求 |
| 这个作业的目标 | 熟悉单元测试和个人开发 |
| PSP2.1 | Personal Software Process Stages | 预估耗时（分钟） | 实际耗时（分钟） |
|---|---|---|---|
| Planning | 计划 | 30 | 40 |
| ·Estimate | ·估计这个任务需要多少时间 | 30 | 40 |
| Development | 开发 | 200 | 365 |
| ·Analysis | ·需求分析（包括学习新技术） | 20 | 30 |
| ·Design Spec | ·生成设计文档 | 15 | 30 |
| ·Design Review | ·设计复审 | 15 | 15 |
| ·Coding Standard | ·代码规范（为目前的开发制定合适的规范） | 5 | 10 |
| ·Design | ·具体设计 | 30 | 50 |
| ·Coding | ·具体编码 | 80 | 180 |
| ·Test | ·测试（自我测试，修改代码，提交修改） | 35 | 50 |
| Reporting | 报告 | 75 | 85 |
| ·Test Report | ·测试报告 | 15 | 20 |
| ·Size Measurement | ·计算工作量 | 10 | 15 |
| ·Postmortem&Process Improvement Plan | ·事后总结，并提出过程改进计划 | 50 | 50 |
| ·合计 | 305 | 495 |
原理介绍
余弦相似度
余弦相似度，又称为余弦相似性，是通过计算两个向量的夹角余弦值来评估他们的相似度。对于两个向量，可以想象成空间中的两条线段，都是从原点（[0, 0, ...]）出发，指向不同的方向。两条线段之间形成一个夹角：如果夹角为0度，则意味着方向相同、线段重合；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。
对n维向量A，B，假设A= [A1, A2, ..., An] ，B= [B1, B2, ..., Bn] ，则A与B的夹角θ的余弦等于：
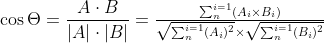
余弦值的范围在[-1,1]之间，值越趋近于1，代表两个向量的方向越接近；越趋近于-1，他们的方向越相反；接近于0，表示两个向量近乎于正交。
一般情况下，相似度都是归一化到[0,1]区间内，因此余弦相似度表示为 cosine_similarity = 0.5cosθ + 0.5
算法实现
这次使用的是python。原本实在c++，java，python中做选择，最后选择了python，算法方面使用了jieba分词库，在余弦相似度与simhash中选取余弦相似度来编写。
部分代码
关于余弦相似度的计算代码
计算机模块接口部分的性能改进
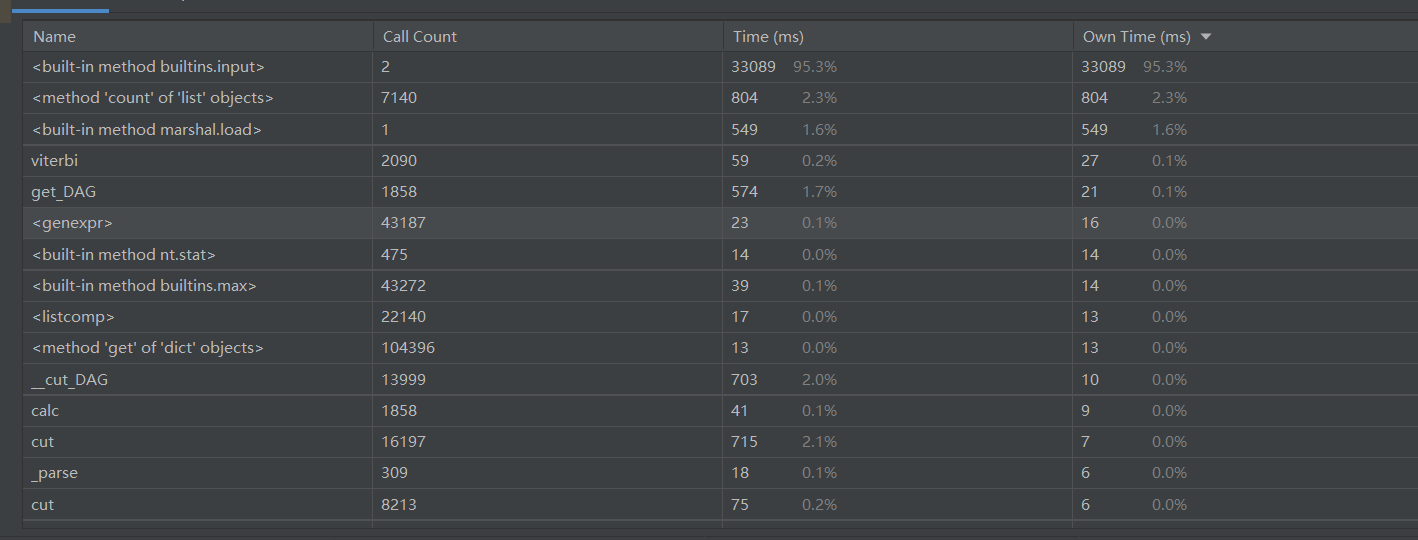
由于只是词性分词而非语义分词，如果需要提高性能，需要换TD—-IDF甚至使用机器学习去进行改进
覆盖率以及部分单元测试
检测空文档
文本对比
