easy 方法记录

原题链接

easy

题目背景

gyy懒得给这题也写个背景......不如直接看题吧。

性质题，我评个紫不过分把

题目描述

有一个字符串 $t$，初始为空。
现在，要对其进行 $n$ 次操作，每次操作首先给出一个字符 $c$：

若 $t$ 为空，则令 $t=cc$。
否则，交换 $t$ 的第 $2,3$ 个字符，第 $4,5$ 个字符......第 $|t|-2,|t|-1$ 个字符；之后，再将 $c$ 分别插
入的第 $2$ 位和倒数第 $2$ 位。

gyy觉得这个操作十分有意思。经过观察，他发现，每次操作完后，$t$ 都是一个偶回文串！

不仅如此，他还发现，$t$ 的偶回文前缀也特别多。所以，他想让你统计一下每次操作之后偶回文前缀的个数。

但他转念一想，这似乎对你来说太简单了。于是，他改为要求你统计每次操作之后偶回文前缀的哈希值之和，并强制在线地回答询问。

同时，他给出了一个数字 $k$ 用来减小输出量。你只需要每次操作后输出一个数表示这 $k$ 次操作的答案的异或和即可。

具体细节或者一些可能出现的疑问请参见输入输出格式及说明。

输入格式

第一行一个字符串 $s$。

第二行一个数 $k$ 用于减小输出量。

强制在线方式：记第 $i$ 次操作后答案为 $ans_i$，则第 $i$ 次操作给出的字符 $c=(ans_{i-1}+s_i-\text{ASCII}(a))\bmod 26+\text{ASCII}(a)$
。特别规定 $ans_0=0$。

输出格式

你要输出 $\lfloor \frac{|s|}{k}\rfloor$ 行，第 $i$ 行表示 $ans_{k(i-1)+1}\ \text{xor}\cdots \text{xor} \ ans_{ki}$。

哈希方式：选取 $B=131$ 为底数，$MOD=2^{64}$ 为模数，则一个字符串 $s$ 的哈希值为：$(\sum_{i=1}^{|s|}(\text{ASCII}(s_i)-\text{ASCII}(a))B^{|s|-i})\bmod MOD$

例如，"abc" 的哈希值为 $(0\times B^2+1\times B^1+2\times B^0)\bmod MOD=133$。

样例 #1

样例输入 #1

abyzuv
1

样例输出 #1

0
17292
2265252
5092492668516
667116539575596
5552418600567558216

样例 #2

样例输入 #2

ctagqkeu
2

样例输出 #2

4894148
1324957402927832
7501175624655915608
7097807190249508344

提示

样例1解释

第1次操作，$c=a$，操作后 $t=aa$，有一个偶回文前缀 $aa$。

第2次操作，$c=b$，操作后 $t=abba$，有一个偶回文前缀 $abba$。

第3次操作，$c=a$，操作后 $t=aabbaa$，有两个偶回文前缀 $aa$ 和 $aabbaa$。

第4次操作，$c=b$，操作后 $t=abbaabba$，有两个偶回文前缀 $abba$ 和 $abbaabba$。

第5次操作，$c=a$，操作后 $t=aabbaabbaa$，有三个偶回文前缀 $aa,aabbaa,aabbaabbaa$。

第6次操作，$c=b$，操作后 $t=abbaabbaabba$，有三个偶回文前缀 $abba,abbaabba,abbaabbaabba$。

数据范围和提示

对于前 $30\%$ 的数据，$|s|\le1000$。

对于前 $50\%$ 的数据，$|s|\le{10}^5$。

对于所有的数据，$1\le k\le |s|\le 5\times {10}^6$。

以下是一些定义：

$|s|$ 表示字符串 $s$ 的长度。

$s_i$ 表示字符串 $s$ 的第 $i$ 个字符，从 $1$ 开始编号。

回文串是指满足 $\forall 1\le i\le |s|,s_i=s_{|s|+1-i}$ 的字符串。

“偶回文串”是指长度为偶数，且是回文串的字符串。

“偶回文前缀”是指是偶回文串且是原串前缀的字符串

题解

思路分析

强制在线就是个幌子，实际上我们完全可以先把$ans_i$都计算出来，然后再根据$k$异或得答案。

题目说要对字符串$t$进行操作，那是不是意味着需要将$t$求出来，然后不断地维护？其实没必要。这道题中蕴含的多种性质可以使我们在$O(n)$的效率处理出$ans_i$.

性质1：字符串$t$的奇数位是原串，偶数位是原串的反串。

解释：

看到题面中样例1的解释，每次操作会首先按照题意计算出一个字符$c$，这些字符$c$组成的字符串就是原串。比如样例1经过4次操作后的原串就是$abab$，反串就是$baba$，而此时的$t$串是$abbaabba$，观察$t$的奇数位和偶数位。

不妨再考虑更一般的情况，下面“输入”一行的数仅表示第几次输入的数，如“1”就表示第一次输入的数。

不难察觉到这种性质的普遍存在。

说明

想想$t$串是如何生成的，基本可以概括为两个操作：交换和插入。（不考虑第一次操作，且首尾位不参与交换）而插在倒数第2位的数不会对前面数的序列号产生影响，重点来注意插在第2位的数——它会使后面数的序列都+1。

在此理解下，奇数位发生交换向前移一位，前面又插入一个数，位置不变；偶数位发生交换向后移一位，前面又插入一个数，位置后移2位。换句话说，奇数位位置不变，所以就是原串；偶数位在操作过程中不断后移，第$i$个输入的偶数位的数截至第$j$次操作共会向后移动$(j-i)*2$位，最终落到的位置构成了反串。

使用

考虑每个数位权的变化。正如十进制数的“个、十、百、千、万”，字符串的哈希值也有位权——这个位置就是$B$次幂。

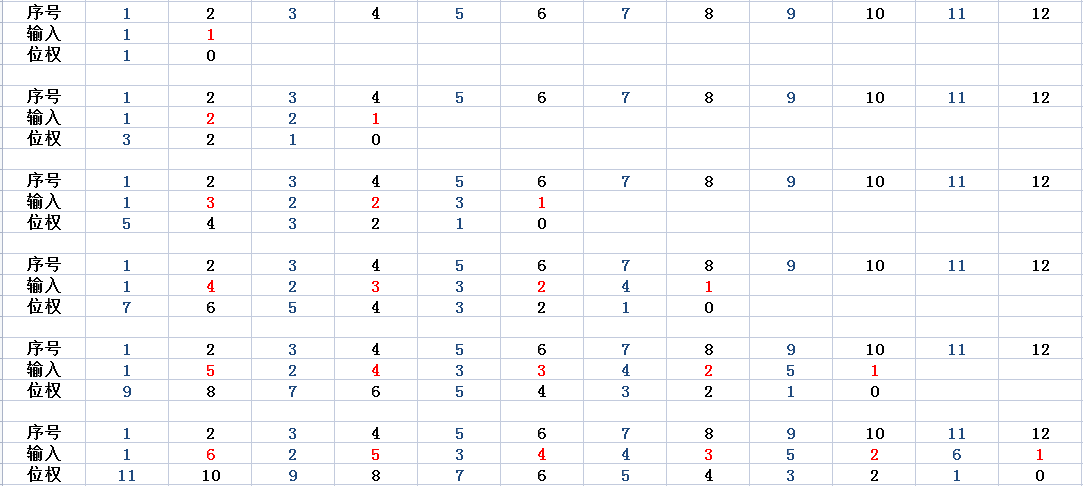
我们声明三个一维数组$h1,h2,mi$，$h1$用于记录奇数位的哈希值之和，$h2$用于记录偶数位的哈希值之和，$mi$的含义是“幂”，用于处理位权的变化。

为了方便处理，我们直接将输入字符串$s$的第$i$位$s_i$变成每次用于操作的$c$字符，即($ull$指$unsigned long long$，自动对$2^64$取模)：

$s[i]=(s[i]-'a'+ull(ans[i-1]%26))%26+'a'$

奇数位上的数每次位置不变，但由于插入了2个数，所以位权翻了两个$B$。而$h1$为了统计奇数位上的哈希值之和，需要对上一个状态乘$B^2$，再加上新增的数（注意倒数第2位的位权），即：

$h1[i]=h1[i-1]*B*B+(s[i]-'a')*B$

偶数位上的数每次位值后移2位，但由于插入了2个数，所以位权不变。而$h2$为了统计偶数位上的哈希值之和，只用在上一个状态的基础上，加上插入到第2位的数的哈希值。$mi$的主要作用也是计算第2位数的哈希值。考虑这个数的维权，在进行第$n$次操作时，$t$串长度为$2*n$，第2位数后面就还有$2*n-2$个位，就可以依此计算，即：

$mi[i]=mi[i-1]*B*B$

$h2[i]=h2[i-1]+(s[i]-'a')*mi[i-1]$

那么将$h1[i]$和$h2[i]$加起来是不是就得到了$ans[i]$？等等，还有一个需要注意的点，$t$串的子串也可能是偶回文前缀！如何处理？看看下一条性质。

性质2：用$KMP$算法对原串进行自我匹配，得到$next$数组，$ans[i]$就应该加上$ans[next[i]].

解释

原串的定义见上，原串即每次用于操作的字符组成的字符串。由于我们直接将$s_i$改写成第$i$次操作的字符，所以我们只用对$s$跑$KMP$求$next$即可。

复习：$next[i]$的定义是，在字符串中以第$i$位结尾的非前缀子串与字符串前缀的最大匹配长度，不了解的看我的这篇博客

我们以第5次操作为例。字符串$ababa$跑$KMP$，得到$next[5]=3$.（即与$aba$匹配）而第3次操作的结果，正是第5次所得字符串子串的最大偶回文前缀（因为$KMP$求的是最大匹配，所以得到的也是最大偶回文前缀），即$aabbaa$，第5次答案累加之。那更小的偶回文前缀，如$aa$怎么办？放心，因为$aabbaa$子串的最大偶回文前缀即是$aa$，所以在处理第3次操作时就已经累加上了$aa$，自然这个结果也被累加到了第5次操作的结果中，则：

$ans[i]=ans[nex[i]]+h1[i]+h2[i]$

说明

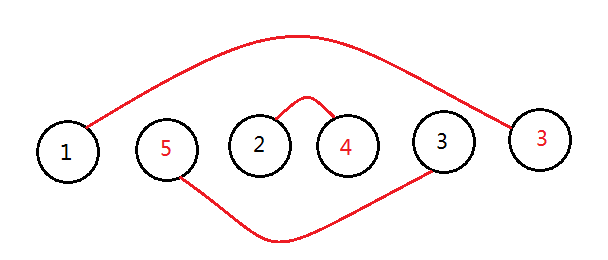
上文说到，$next[5]=3$，该匹配是这样的（数字表示序号）：

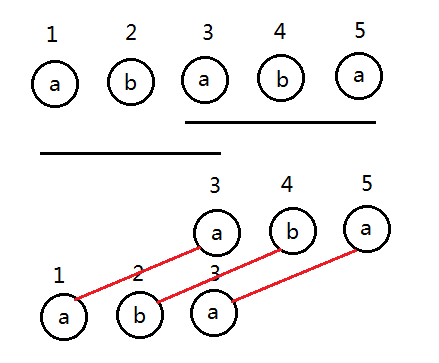
由性质1及其解释，我们知道所谓“原串”其实就是$t$串的奇数位，而$t$串就可以理解为在原串的两数间隙中插入一个反串。

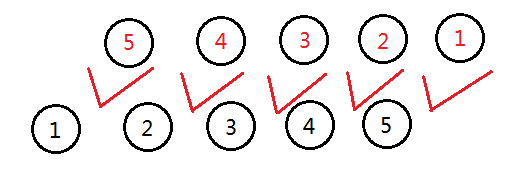
把两张图结合起来看，一个串能和另一个串匹配，说明字符是对应相同的。那么它和那个串的反串是不是也存在字符的相同性？

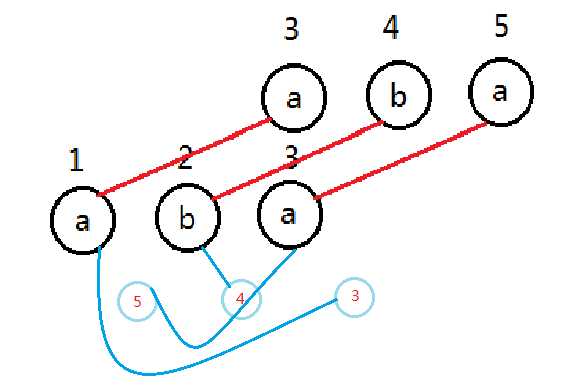
将它展开来看，一个偶回文前缀便诞生了。

最后，用$k$对$ans_i$进行异或压缩即可。

AC代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef unsigned long long ull;
const ull N=5000005;
const ull B=131;
char s[N];
ull nex[N],mi[N],h1[N],h2[N],ans[N];
ull k,len,num;
template <typename T>inline void re(T &x) {
	x=0;
	ull f=1;
	char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-f;
	for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^48);
	x*=f;
	return;
}
template <typename T>void wr(T x) {
	if(x<0) putchar('-'),x=-x;
	if(x>9) wr(x/10);
	putchar(x%10^'0');
	return;
}
signed main()
{
	scanf("%s",s+1);
	scanf("%lld",&k);
	len=strlen(s+1);
	mi[1]=B*B;
	h1[1]=(s[1]-'a')*B;
	h2[1]=s[1]-'a';
	ans[1]=h1[1]+h2[1];
	nex[1]=0;
	for(ull i=2,j=0;i<=len;i++)
	{
		s[i]=(s[i]-'a'+ull(ans[i-1]%26))%26+'a';
		while(j>0&&s[i]!=s[j+1]) j=nex[j];
		if(s[i]==s[j+1]) j++;
		nex[i]=j;
		mi[i]=mi[i-1]*B*B;
		h1[i]=h1[i-1]*B*B+(s[i]-'a')*B;
		h2[i]=h2[i-1]+(s[i]-'a')*mi[i-1];
		ans[i]=ans[nex[i]]+h1[i]+h2[i];
	}
	for(ull i=1;i<=len;i++)
	{
		num^=ans[i];
		if(i%k==0)
		{
			wr(num);
			puts("");
			num=0;
		}
	}
	return 0;
}

posted @ 2022-10-20 10:30 Fish4174 阅读(73) 评论(2) 收藏举报

刷新页面返回顶部

fish4174