Python基础讲义（一）：数值类型与运算

0x01内容导图

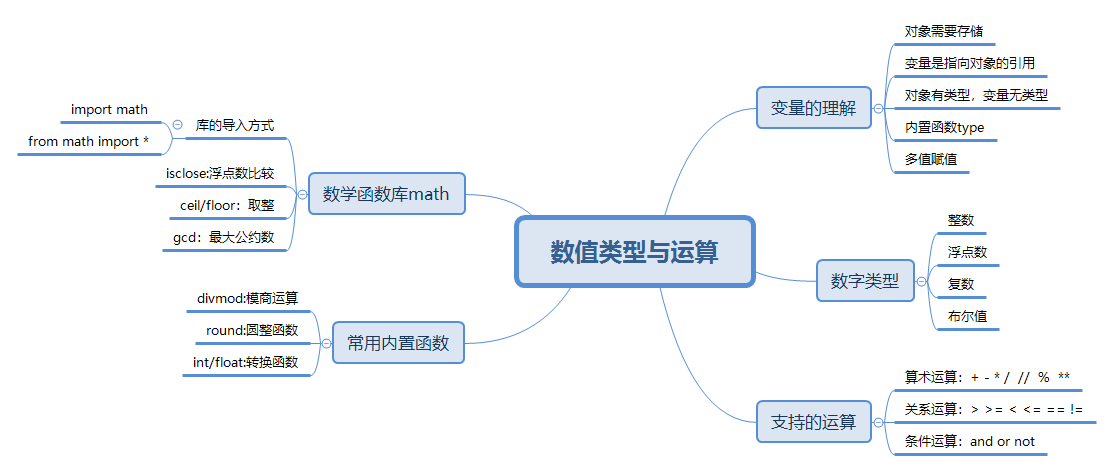
0x02变量的理解

• 对象包含类型和值，对象存储需要内存
• 字面量，一次使用
• 定义变量实质是将对象地址与变量绑定，方便多次使用
• 变量名是内存地址的别名，即指向对象的引用
• 变量本身无类型，它指向的对象有类型
• 变量定义语法：
  • 变量名 = 初值
  • Python支持多值赋值，x, y... = 1, 2, ...
• 内置函数type：获取对象类型；内置函数id：获取对象id，唯一性标志

代码示例

>>> type(3)			#获取对象3的类型
<class 'int'>
>>> x = 3			#变量名x与对象3绑定，通过x可访问到对象3
>>> x + 5
8
>>> id(x)
1674433616			#对象id，具体数据与本地机器相关
>>> x, y = 3, 5		        #Python特有的多值赋值
# 有了这个特性，交换变量的值变得很简单
>>> x, y = y, x
>>> x, y
(5, 3)

• 标识符命名规则：
  • 第一个字符必须是字母表中字母或下划线 _
  • 标识符的其他的部分由字母、数字和下划线组成
  • 标识符对大小写敏感
  • 不能与关键字相同

0x03数值类型

• 整数：十进制、十六进制、二进制表示；理论上无限大(受内存限制)
• 浮点数：64位，双精度，有误差；可以使用科学计数法
  • 1/2 + 1/3 + 1/6，不是精确的1
  • 0.1+0.2，不等于0.3
  • x = 1.2e3
• 复数：用于科学计算；虚部用j表示
• 布尔类型：逻辑值，True或者False

代码示例

>>> a = 0x12				#十六进制
>>> a
18
>>> 0b11					#二进制
3
>>> 2 ** 100				#天然支持大数，2的100次方
1267650600228229401496703205376
>>> 1/2 + 1/3 + 1/6
0.9999999999999999

0x04表达式运算

• 算术运算
  • +、-、*、**（幂运算）；/（数学意义上的除法）、//（整除取商）、%（整除取余）
  • 扩展关系：整数->浮点数->复数，运算结果与参与运算的高级操作数保持一致
  • 复合赋值：a = a op b => a op= b，书写简便、高效
  • 模运算理解：越界翻转，周期特点

代码示例

>>> m = 137			#分钟，转换为（小时，分）
>>> hs, ms = m // 60, m % 60
>>> hs, ms
(2, 17)
>>> x = 5
>>> x += 3			#相当于x = x + 3，推荐使用复合赋值

• 关系运算
  • 六种：>、>=、<、<=、==、!=
  • 运算结果为布尔类型
  • 注意判等运算与赋值运算在形式上的区别
• 条件运算
  • 三种：条件与and、条件或or、条件非not
  • 运算结果为布尔类型
  • 短路效应

代码示例

>>> x, y = 10, 5
>>> x > y
True
>>> x, y = 75, "女"
>>> y == "女" and x >= 60			#思考两个条件的顺序
True
#闰年判断表达式
>>> y = 2000
>>> y % 400 == 0 or (y % 4 == 0 and y % 100 != 0)
True

0x05常用内置函数

• divmod(x, y)：模商同时运算
• round(x[, 精度])：四舍五入。注意：中间值，向偶数舍
• int/float(x)：转换函数

代码示例

>>> x, y = divmod(137, 60)
>>> x, y
(2, 17)
>>> round(2.5)
2
>>> round(3.5)
4
>>> int("3")
3
>>> int(3.8)							#浮点数转整数，截断
3

0x06数学函数库

• 引用库的方式：
  • import math
  • from math import *
• 常用函数
  • ceil(x)：向上取整
  • floor(x)：向下取整
  • gcd(x, y)：返回最大公约数
  • isclose(x, y)：浮点数比较，可选参数rel_tol（相对误差），abs_tol（绝对误差）

代码示例

>>> import math
>>> math.ceil(2.1)
3
>>> math.floor(2.9)
2
>>> math.gcd(24, 18)
6
>>> math.isclose(2.0, 2.001, abs_tol = 0.001)
True
#一元二次方程求解
>>> a, b, c = 1, -2, -3
>>> delta = math.sqrt(b*b - 4 * a * c)
>>> x1 = (-b + delta) // 2 * a
>>> x2 = (-b - delta) // 2 * a
>>> x1, x2
3.0, -1.0

0x07小结

• 理解变量的意义
• 熟悉数值类型及其运算
• 熟练掌握常用内置函数
• 掌握标准库的导入，熟练掌握math库常用函数