算法导论：图论

基本概念

二分图

一个二分图是一个无向图 \(G = (V,E)\)，其中 \(V\) 可以划分为 2 个集合 \(V_1\) 和 \(V_2\)，且对于任意条边 \((u, v)\in E\)，都有 \(u \in V_1\) 且 \(v\in V_2\)，或者 \(v\in V_1\) 且 \(u\in V_2\)

树

令 \(G=(V,E)\) 为一个无向图，如果 \(G\) 是一颗树，则满足以下性质：

• \(G\) 中的任意 2 个节点都有唯一的连通路径
• \(G\) 是连通的，且 \(|E|=|V|–1\)，但是从 \(G\) 中删除任意一条边后 \(G\) 都将不连通
• \(G\) 是无环的，但是如果任意加一条边至 \(G\) 中，则会在 \(G\) 中生成一个有环

DFS 应用

边的分类

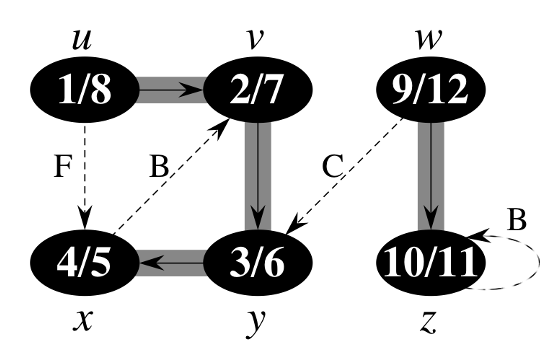
• 树边：属于 \(DFS\) 森林的边
• 反向边：从一个节点连向它在 DFS 树中的祖先节点的非树边，如边 \(B\)
• 前向边：从一个节点连向它在 DFS 树中的后代节点的非树边，如边 \(F\)
• 交叉边：图中不属于树边、反向边、和前向边的那些边，如边 \(C\)

无向图 \(G\) 是否连通

调用一次 \(DFS\)，然后检查图中是否还有节点未访问。如果没有，则图连通，否则不连通。

运行时间 \(O(|V|+|E|)\)

寻找连通分支

每次调用 \(DFS\)，其中所有遍历到的节点属于一个连通分支。

运行时间 \(\Theta(|V|+|E|)\)

一个有向图 \(G\) 中是否包含一个有向环

调用 \(DFS\)，如果存在反向边，则存在有向环，否则不存在。

运行时间 \(O(|V|+|E|)\)

一个无向图 \(G\) 中是否包含一个环

调用 \(DFS\)，如果存在反向边，则存在环，否则不存在。

如果图 \(G\) 是一个树或者森林，则它最多包含 \(|V |–1\) 条边。运行时间为 \(O(|V|)\) ，因为 DFS 算法在发现环之前最多只会遍历 \(|V|\) 条边（一个无向图如果有 \(\geq|V|\) 条边，则一定有环）。

无向图 \(G\) 是否是一颗树

调用一次 \(DFS\)，如果所有的边都遍历了，且没有反向边，则图 \(G\) 是一颗树。

运行时间 \(O(|V|)\)

拓扑排序

方法一

• 调用 \(DFS\) 计算每个节点被 \(DFS\) 访问的结束时间
• 以节点结束时间从大到小的顺序输出节点

运行时间 \(\Theta(|V|+|E|)\)

方法二

• 找到一个没有入边的节点
• 删除该节点和与该节点相连的边
• 重复前面步骤
• 删除节点的顺序即为一个拓扑序

运行时间 \(O(|V|+|E|)\)

强连通分支

一个有向图 \(G=(V,E)\) 的强连通分支是一个最大的节点集合，该集合中的任意节点互相连通。

1、调用 \(DFS(G)\)，计算被 \(DFS\) 访问的结束时间

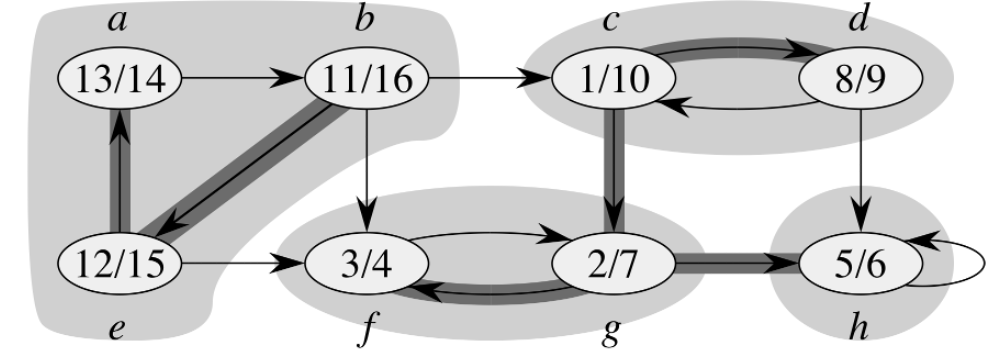
2、计算 \(G\) 的转置

有向图的转置：令 \(G=(V,E)\) 为一个有向图，\(G\) 的转置为 \(G^T=(V,E^T)\)，其中 \(E^T=\left\{(u,v):(v,u)\in E\right\}\)

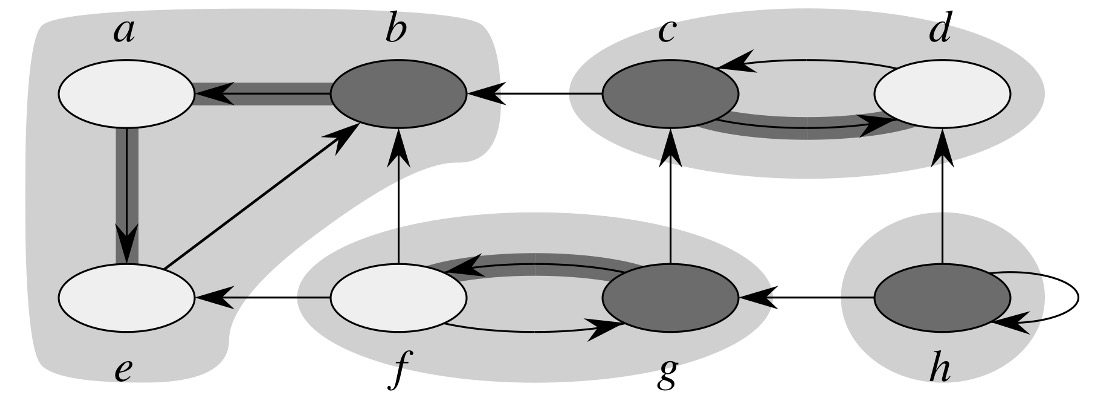
3、调用 \(DFS(G^T)\)，在 \(DFS\) 的主循环中，以节点结束时间下降的顺序遍历节点，即先考虑 \(b\)，然后 \(c,g,h\)。输出的 \(DFS\) 树，每颗 \(DFS\) 树中的节点形成一个强连通分支。

生成树

对于一个连通的无向图 \(G=(V,E)\)，它的生成树是指包含图 \(G\) 中所有节点的树。

对于一个连通无向的加权 \(G\)，它的最小生成树指的是权值最小的生成树。

并查集

一个并查集维护了一个由一系列互相不相交的集合构成的集合 \(S=\left\{S_1,S_2,…,S_k\right\}\)，支持的操作如下：

• \(Make-Set(x)\)：对元素 \(x\) 创建一个新的集合 \(S_i=\left\{x\right\}\)，并且把 \(S_i\) 这个集合加入至并查集 \(S\) 中
• \(Find-Set(x)\)：返回包含元素 \(x\) 的集合的那个代表性元素
• \(Union(x,y)\)：其中 \(x\in S_x\)，\(y\in S_y\)，将 \(S_x\) 和 \(S_y\) 两个集合合并称一个集合

数据结构

除了使用数组的方式来实现并查集，也可以使用类似链表的结构来实现。

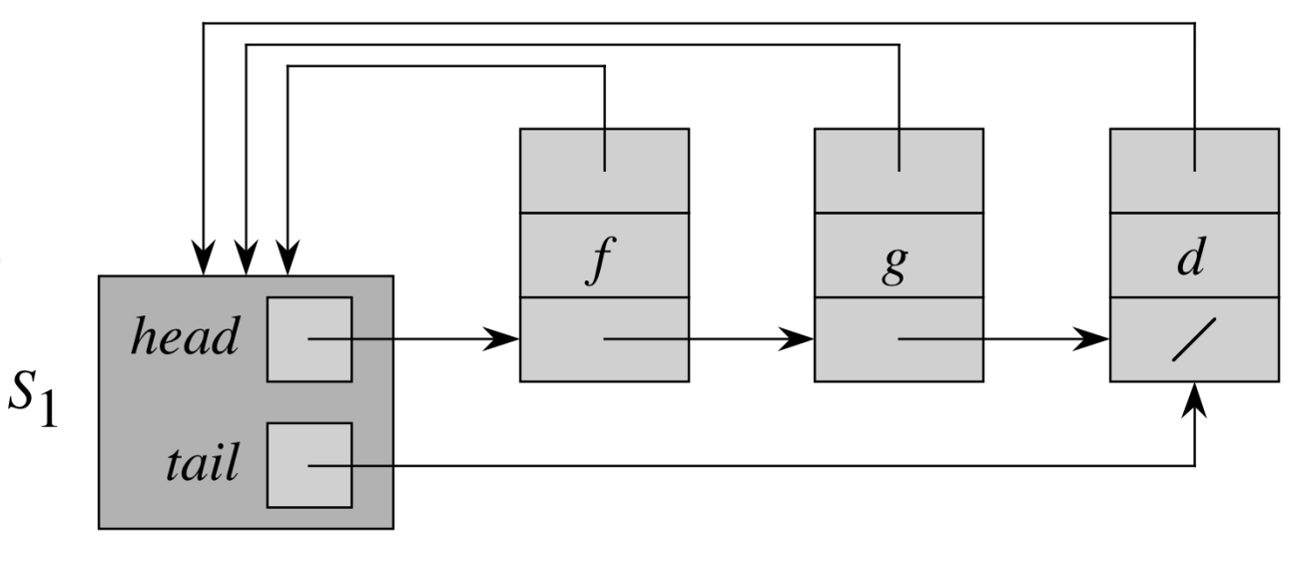
链表中的第一个元素（\(head\) 指向的元素）为集合的代表性元素。

• \(Make-Set(x)\)：\(O(1)\)
• \(Find-Set(x)\)：\(O(1)\)，因为每个元素都指向了 \(head\)
• \(Union(x,y)\)：\(O(n)\)

并查集应用：寻找无向图中所有的连通分支

1. 将无向图中的每个节点都初始化为一个集合（连通分支）
2. 遍历无向图中的每条边，将边两端的节点所在的集合进行合并

Kruskal 算法

算法思路

1. 初始化：每个节点为一个连通分支。
2. 按照权值递增的顺序选择边，利用一个并查集的数据结构来判断一条边的两个端点是否属于不同的连通分支，如果是，则合并两个连通分支。
3. 重复第二步操作。

伪代码

• 初始化 \(A\)：\(O(1)\)
• 第一个 \(FOR\) 循环：有 \(|V|\) 个 \(Make-Set\) 操作，总时间代价为 \(O(|V|)\)
• 边排序的代价：\(O(|E|lg|E|)\)
• 第二个 \(FOR\) 循环：\(O(|E|)\) 个 \(Find-Set\) 操作，每个的代价为 \(O(1)\)。\(O(|E|)\) 个 \(Union\) 操作，每个的代价可以做到 \(O(lg|V|)\)
• 总的时间复杂度：\(O(|E|lg|E|)\) 或者 \(O(|E|lg|V|)\)

Prim 算法

算法思路

1. 初始时，可以选择任意的一个节点为树的根节点。
2. 在每一步中，将跨越集合 \(V_A\) 和集合 \(V–V_A\) 权值最小的边加入 \(V_A\) 中，\(V_A\) 表示局部树的节点集合。

使用邻接表来表示图比较合理：因为当加入某个节点到 \(V_A\) 中时，该节点的邻居到 \(V_A\) 的距离可能会减少，需要重新计算距离，所以需要快速访问节点的邻居。

用最小优先队列（小顶堆）来实现 \(Q\) 快速找到权值最小的边：

• \(Q\) 中的元素是一个非局部树节点，即 \(V–V_A\) 中的节点
• \(Q\) 中的元素 \(u\) 的优先级为权值最小的边 \((u,v)\) 的权值，其中 \(v\in V_A\)
• 当 \(V_A\) 中的节点越来越多时，节点 \(u\) 的优先级可能会变小
• 调用 \(Extract-Min(Q)\) 操作表示从 \(Q\) 中取 \(key\) 值最小的节点
• 如果一个节点不与 \(V_A\) 中的节点相连，则它的 \(key\) 值为 \(\infty\)

伪代码

• 初始化 \(Q\)（小顶堆）和第一个 \(FOR\) 循环的代价：\(O(|V|)\)
• \(WHILE\) 循环 \(|V|\) 次：
  • \(Extract-Min\)：\(O(lg|V|)\)
  • \(FOR\) 一共 \(O(|E|)\) 次，除了 \(DECREASE-KEY\) 需要 \(O(lg|V|)\)，其余需要 \(O(1)\)
• 整个 \(WHILE\) 循环：\(O(|V|lg|V|)+O(|E|lg|V|)=O(|E|lg|V|)\)