算法导论：分治算法

效率分析

迭代法

求n！

int fact(int n) {
	if(n <= 1) return 1;
  else return n * fact(n-1);
}

递归关系式：

\[T(n)= \begin{cases} 1, & n=1\\ T(n-1)+1, & n>1 \end{cases} \]

分析：

\[\begin{align} T(n)&=T(n-1)+1 \\ &=T(n-2)+1+1 \\ &=... \\ &=T(1)+1+...+1 \\ &=T(1)+n-1 \\ &=n \end{align} \]

所以 \(T(n)\in\Theta(n)\)

归并排序

MERGE-SORT(A, p, r)
if(p < r) {
	q = (p + r) / 2;
  MERGE-SORT(A, p, q);
  MERGE-SORT(A, q + 1, r);
  MERGE(A, p, q, r);
}

递归关系式：

\[T(n)= \begin{cases} 1, & n=1\\ 2T(n/2)+n, & n>1 \end{cases} \]

分析：

\[\begin{align} T(2^k)&=2T(2^{k-1})+2^k \\ &=2(2T(2^{k-2})+2^{k-1})+2^k \\ &=2^2T(2^{k-2})+2^k+2^k \\ &=... \\ &=2^kT(2^{k-k})+2^k+...+2^k \\ &=2^k+k2^k \end{align} \]

所以 \(T(n)\in\Theta(nlogn)\)

递归树法

• 递归树给出了递归算法中各个过程运行时间的估计。
• 递归式 \(T(n)=kT(n/m)+f(n)\) 中每次递归调用用一个结点表示，结点包含非递归操作次数 \(f(n)\)。
• 每层的右侧标出当前层中所有节点的和。
• 将所有层总的操作次数相加。

归并排序递归树

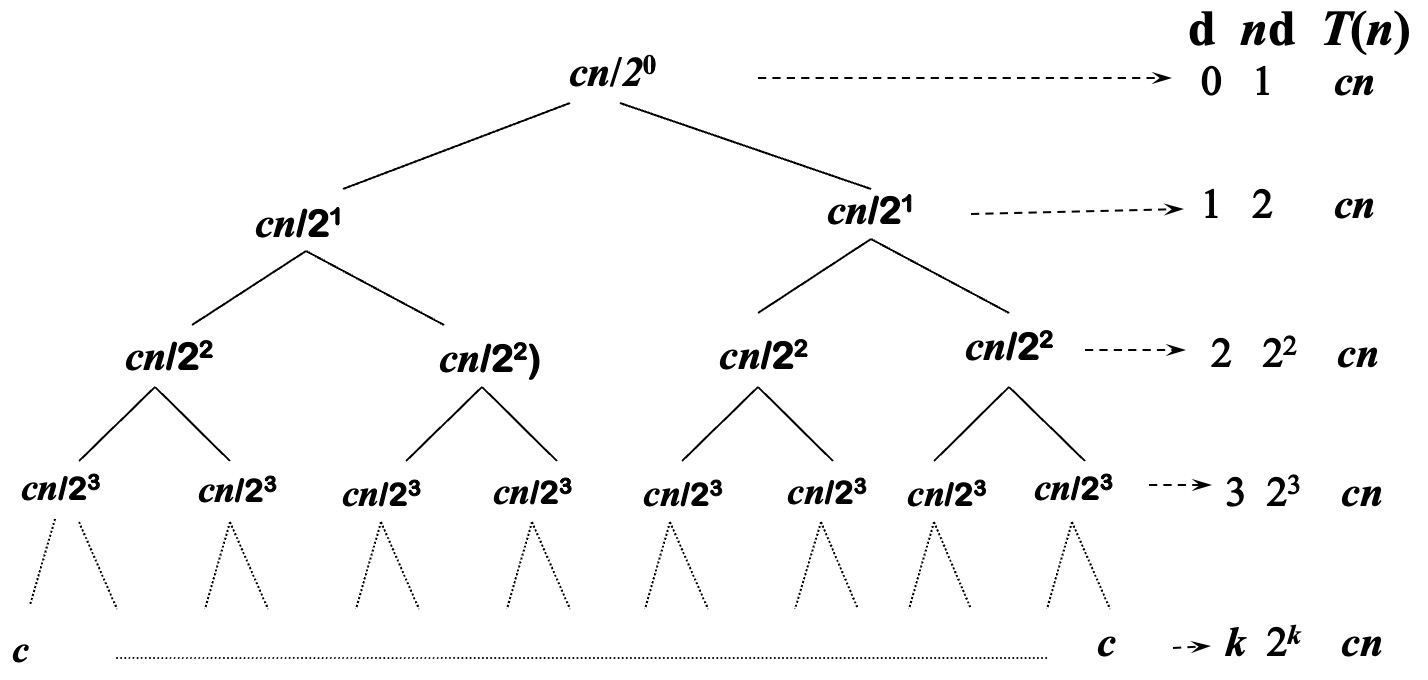
• 右侧 \(d\) 表示树的深度，\(nd\) 表示该层节点数，\(T(n)\) 表示该层的代价。
• 初始的，递归树只有一个结点，最坏情况下的合并代价是 \(cn\)。
• 在第 \(k\) 层时，归并排序输入的规模为 \(n/2k=1\)，该节点为叶子结点，代价是 \(\Theta(1)\)。
• 总代价 \(T(n)=(k+1)cn=(lgn+1)cn=\Theta(nlgn)\)

主定理法

该方法可解如下形式的递归式：\(T(n)=aT(n/b)+f(n)\)，其中 \(1\leq{a},1<b,f(n)\) 是渐进非负函数。

如果 \(n/b\) 不是整数，则取整，可以向上也可以向下。

\[T(n)= \begin{cases} \Theta(n^{log_ba}), & f(n)\in{O(n^{log_ba-\epsilon})},\epsilon>0 & (1)\\ \Theta(n^{log_ba}lg^{k+1}n), & f(n)\in{\Theta(n^{log_ba}lg^kn)},k>0 & (2)\\ \Theta(f(n)), & f(n)\in{\Omega(n^{log_ba+\epsilon})},\epsilon>0,af(n/b)<cf(n),c<1 & (3) \end{cases} \]

关键是看 \(f(n)\) 和 \(n^{log_ba}\) 谁比较大。

（1）成立时，如果 \(n^{log_ba}\) 比较大，则 \(T(n)=\Theta(n^{log_ba})\)。

\[T(n)=8T(n/2)+1000n^2 \\ a=8,b=2,f(n)=1000n^2 \\ f(n)\in{O(n^c)},c=2 \\ log_ba=log_28=3>c=2 \\ T(n)\in{\Theta(n^{log_ba})}=\Theta(n^3) \]

（2）成立时，如果 \(f(n)\) 和 \(n^{log_ba}lg^kn\) 大小相当，则 \(T(n)=\Theta(n^{log_ba}lg^{k+1}n)\)。

\[T(n)=2T(n/2)+10n \\ a=2,b=2,c=1,f(n)=10n \\ f(n)\in{\Theta(n^clog^kn)},c=1,k=0 \\ log_ba=log_22=1,c=log_ba \\ T(n)=\Theta(n^{log_ba}lg^{k+1}n)=\Theta(n^1log^1n)=\Theta(nlogn) \]

（3）成立时，如果 \(f(n)\) 比较大，则 \(\Theta(f(n))\)。

\[T(n)=2T(n/2)+n^2 \\ a=2,b=2,f(n)=n^2 \\ f(n)=\Omega(n^c),c=2 \\ log_ba=log_22=1,c>log_ba \\ 2(n^2/4)<kn^2,选择k=1/2 \\ T(n)=\Theta(f(n))=\Theta(n^2) \]

• \(f(n)\) 可以理解为把一个规模为 \(n\) 的问题分解成 \(a\) 个规模为 \(n/b\) 的子问题和合并 \(a\) 个子问题的解的代价。
• \(af(n/b)\) 可以理解为把 \(a\) 个规模为 \(n/b\) 的子问题分解成 \(a^2\) 个规模为 \(n/b^2\) 的子问题和合并 \(a^2\) 个子问题解的代价。
• 正则条件 \(af(n/b)<cf(n),c<1\) 可以理解为当一个问题被分解成越来越小的子问题，分解和合并的代价变得越来越小。

改变变量：有时代数操作可以把一个未知的递归式转换成已知可解的递归式。

\[T(n)=2T(\sqrt{n})+lgn \\ m=lgn,n=2^m \\ T(2^m)=2T(2^{m/2})+m \\ S(m)=T(2^m) \\ S(m)=2S(m/2)+m \\ S(m)\in{\Theta{(mlgm)}} \\ T(n)=T(2^m)=S(m)\in{\Theta{(mlgm)}}=\Theta(lgnlglgn) \]

二维最近对问题

问题描述

\(P_1(x_1,y_1),...,P_n(x_n,y_n)\) 是平面上 \(n\) 个点构成的集合 \(S\)，假设 \(n=2^k\)，最近点对问题要求找出距离最近的两个点。

解题思路

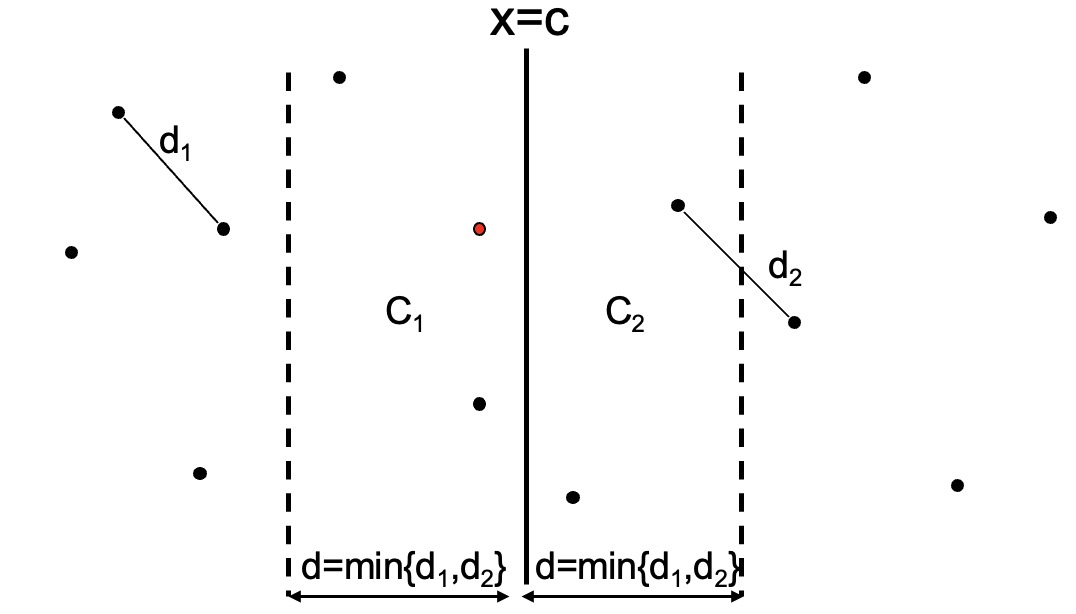
• 将点集 \(S\) 分为 \(S1\) 和 \(S2\)，分隔线是 \(S\) 在 \(x\) 轴的中点（选择最中心的两个点的 \(x\) 轴的平均值）。
• 递归求解 \(S1\) 和 \(S2\) 的最近点对，令 \(d=min\left\{d1,d2\right\}\)，确定 \(C1\) 和 \(C2\)。
• 将 \(C1\) 和 \(C2\) 的最近点对合并。在合并两个子集 \(C1\) 和 \(C2\) 时，对于 \(C1\) 中的每个点 \(P(x,y)\)，都须要检查 \(C2\) 中的点和 \(P\) 之间的距离是否小于 \(d\)。

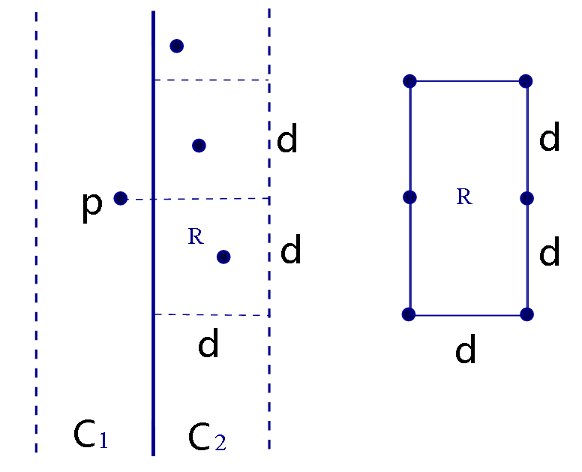
• 假设 \(P\) 在 \(C1\) 中，只需要检查 \(P\) 的上下距离为 \(d\) 的范围内的点是否小于 \(d\)

效率分析

合并最小问题所花的时间为 \(M(n)=O(n)\)

该算法的最差递归时间为：\(T(n)=2T(n/2)+n=O(nlogn)\)

最大连续子数组问题

问题描述

• 输入：数组 \(A[1,...,n]\)，存在负数
• 输出：数组下标 \(i\) 和 \(j\) 使得子数组 \(A[i,...,j]\) 为数组 \(A[1,...,n]\) 的最大非空连续子数组

解题思路

用分治思维解决，子问题为找出 \(A[low,...,high]\) 的最大子数组。

• 初始值 \(low=1,high=n\)
• 分解：将子数组分解成两个大小相当的子数组，\(A[low,...,mid]\) 和 \(A[mid+1,...,high]\)
• 求解：分别找出数组 \(A[low,...,mid]\) 和 \(A[mid+1,...,high]\) 的最大子数组
• 组合：找出跨越中间位置的最大子数组，从找到的三个最大子数组中选择最大的子数组

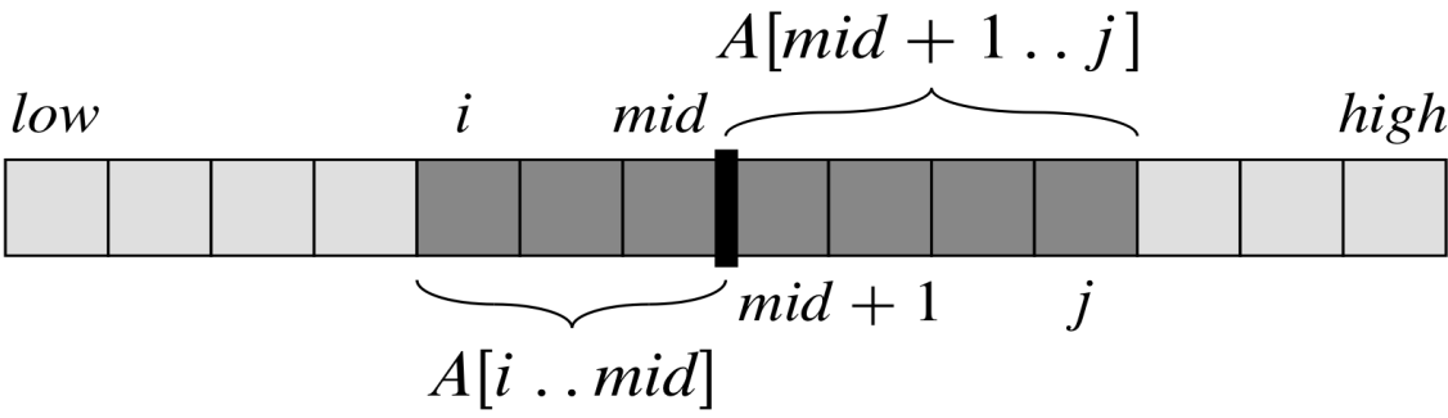
找出跨越中间位置的最大子数组（必须跨越中间位置）。任何一个跨越中间位置 \(A[mid]\) 的子数组 \(A[i,...,j]\) 由两个更小的子数组 \(A[i,...,mid]\) 和 \(A[mid+1,...,j]\) 组成，其中 \(low\leq{i}\leq{mid}<j\leq{high}\)

伪代码

// 找出跨越中间位置的最大子数组
Find-Max-Crossing-SubAarry(A, low, mid, high) {
	// 从 A[i,...,mid] 找到最大子数组
  left-sum = -inf;
  sum = 0;
  for(i = mid; i >= low; i--){
  	sum += A[i];
    if(sum > left-sum) {
    	left-sum = sum;
      max-left = i;
    }
  }
  // 从 A[mid+1,...,j] 找到最大子数组
  right-sum = -inf;
  sum = 0;
  for(j = mid+1; i >= high; i++){
  	sum += A[j];
    if(sum > right-sum) {
    	right-sum = sum;
      max-right = j;
    }
  }
  // 返回下标和两边最大值的和
  return (max-left, max-right, left-sum + right-sum)
}

// 最大子数组问题（分治）
Find-Maximum-SubArray(A, low, high) {
	if(high == low) return (low, high, A[low]);
  else {
  	mid = (low + high) / 2;
    (left-low, left-high, left-sum) = Find-Maximum-SubArray(A, low , mid);
    (right-low, right-high, right-sum) = Find-Maximum-SubArray(A, mid + 1 , high);
    (cross-low, cross-high, cross-sum) = Find-Max-Crossing-SubAarry(A, low, mid, high);
    if(left-sum >= right-sum && left-sum >= cross-sum) return (left-low, left-high, left-sum);
    else if(right-sum >= left-sum && right-sum >= cross-sum) return (right-low, right-high, right-sum);
    else return (cross-low, cross-high, cross-sum);
  } 
}

效率分析

• 当 \(high=low,n=1\) 时，算法直接返回，此时 \(T(n)=\Theta(1)\)

• 当 \(n>1\) 时，需要递归

  • 分解：需要 \(\Theta(1)\) 时间
  • 求解：两个子问题，每个子问题有 \(n/2\) 个元素，需要 \(T(n/2)\) 时间，共 \(2T(n/2)\) 时间
  • 合并：查找跨越中间位置的最大子数组，需要 \(\Theta(n)\) 时间，大小比较需要 \(\Theta(1)\) 时间，共 \(\Theta(n)+\Theta(1)\)

综上：\(T(n)=\Theta(1)+2T(n/2)+\Theta(n)+\Theta(1)=2T(n/2)+\Theta(n)\)

这与递归排序的递归式相同，故 \(T(n)=\Theta(nlgn)\)